- 2021-06-10 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届河北省邯郸市北外附属学校高二上学期第二次月考数学试卷(解析版)
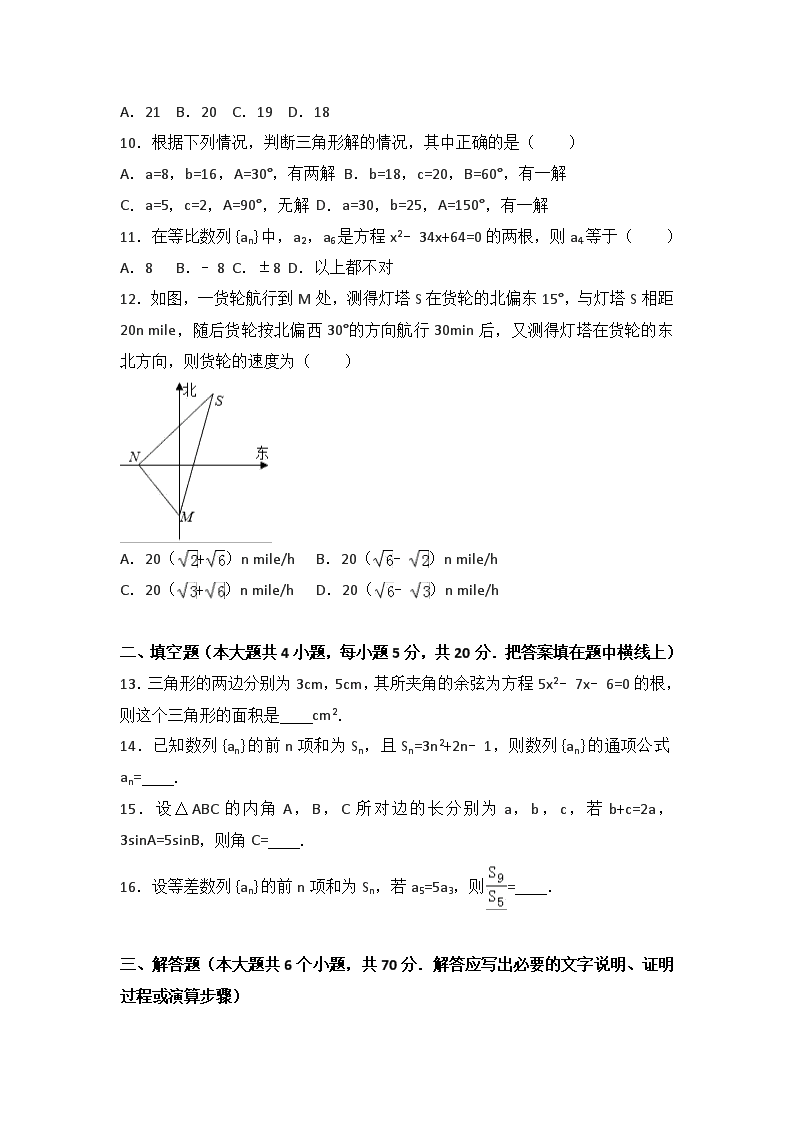
2016-2017学年河北省邯郸市北外附属学校高二(上)第二次月考数学试卷 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知{an}为等差数列,且a7﹣2a4=﹣1,a3=0,则公差d=( ) A.﹣2 B.﹣ C. D.2 2.在△ABC中,AB=5,BC=7,AC=8,则•的值为( ) A.5 B.﹣5 C.15 D.﹣15 3.已知一等比数列的前三项依次为x,2x+2,3x+3,那么﹣13是此数列的第( )项. A.2 B.4 C.6 D.8 4.在△ABC中,cosAcosB>sinAsinB,则△ABC为( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判定 5.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,bc=4,则△ABC的面积为( ) A. B.1 C. D.2 6.等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前n项和Sn=( ) A.n(n+1) B.n(n﹣1) C. D. 7.在△ABC中,b=,c=3,B=30°,则a=( ) A. B.2 C.或2 D.2 8.若{an}是等差数列,首项a1>0,a1007+a1008>0,a1007•a1008<0,则使前n项和Sn>0成立的最大自然数n是( ) A.2 012 B.2 013 C.2 014 D.2 015 9.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( ) A.21 B.20 C.19 D.18 10.根据下列情况,判断三角形解的情况,其中正确的是( ) A.a=8,b=16,A=30°,有两解 B.b=18,c=20,B=60°,有一解 C.a=5,c=2,A=90°,无解 D.a=30,b=25,A=150°,有一解 11.在等比数列{an}中,a2,a6是方程x2﹣34x+64=0的两根,则a4等于( ) A.8 B.﹣8 C.±8 D.以上都不对 12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( ) A.20(+)n mile/h B.20(﹣)n mile/h C.20(+)n mile/h D.20(﹣)n mile/h 二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.三角形的两边分别为3cm,5cm,其所夹角的余弦为方程5x2﹣7x﹣6=0的根,则这个三角形的面积是 cm2. 14.已知数列{an}的前n项和为Sn,且Sn=3n2+2n﹣1,则数列{an}的通项公式an= . 15.设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C= . 16.设等差数列{an}的前n项和为Sn,若a5=5a3,则= . 三、解答题(本大题共6个小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤) 17.已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cosB= (Ⅰ)若b=4,求sinA的值; (Ⅱ) 若△ABC的面积S△ABC=4求b,c的值. 18.已知等差数列{an}中,a10=30,a20=50. (1)求通项公式; (2)若Sn=242,求项数n. 19.在△ABC中,已知内角A=,边BC=2,设内角B=x,周长为y (1)求函数y=f(x)的解析式和定义域; (2)求y的最大值. 20.设各项均为正数的数列{an}的前n项和为Sn,且Sn满足﹣(n2+n﹣3)Sn﹣3(n2+n)=0,n∈N*. (1)求a1的值; (2)求数列{an}的通项公式. 21.在△ABC中,角A、B、C的对边分别为a、b、c,面积为S,已知acos2+ccos2=b (1)求证:a、b、c成等差数列; (2)若B=,S=4 求b. 22.已知数列{an},an∈N*,前n项和Sn=(an+2)2. (1)求证:{an}是等差数列; (2)若bn=an﹣30,求数列{bn}的前n项和的最小值. 2016-2017学年河北省邯郸市北外附属学校高二(上)第二次月考数学试卷 参考答案与试题解析 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知{an}为等差数列,且a7﹣2a4=﹣1,a3=0,则公差d=( ) A.﹣2 B.﹣ C. D.2 【考点】等差数列. 【分析】利用等差数列的通项公式,结合已知条件列出关于a1,d的方程组,求解即可. 【解答】解:设等差数列{an}的首项为a1,公差为d,由等差数列的通项公式以及已知条件得 ,即, 解得d=﹣, 故选B. 2.在△ABC中,AB=5,BC=7,AC=8,则•的值为( ) A.5 B.﹣5 C.15 D.﹣15 【考点】余弦定理;向量在几何中的应用. 【分析】求出B,代入数量积公式即可. 【解答】解:cosB==. ∴=AB•BC•cosB=5. 故选A. 3.已知一等比数列的前三项依次为x,2x+2,3x+3,那么﹣13是此数列的第( )项. A.2 B.4 C.6 D.8 【考点】等比数列的通项公式. 【分析】根据等比数列的性质可知第2项的平方等于第1,第3项的积,列出关于x的方程,求出方程的解,经检验得到满足题意x的值,然后根据x的值求出等比数列的首项和公比,写出等比数列的通项公式,令通项公式等于﹣13列出关于n的方程,求出方程的解即可得到n的值. 【解答】解:由等比数列的前三项依次为x,2x+2,3x+3, 得到(2x+2)2=x(3x+3),即(x+1)(x+4)=0, 解得x=﹣1或x=﹣4,当x=﹣1时,等比数列的前三项依次为﹣1,0,0不合题意舍去, 所以x=﹣4,等比数列的前三项依次为﹣4,﹣6,﹣9, 则等比数列的首项为﹣4,公比q==, 令an=﹣4=﹣13,解得n=4. 故选B 4.在△ABC中,cosAcosB>sinAsinB,则△ABC为( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判定 【考点】三角形的形状判断. 【分析】利用余弦的两角和公式整理题设不等式求得cos(A+B)>0进而判断出cosC<O,进而断定C为钝角. 【解答】解:依题意可知cosAcosB﹣sinAsinB=cos(A+B)>0,﹣cosC>O,cosC<O, ∴C为钝角 故选C 5.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2 ﹣bc,bc=4,则△ABC的面积为( ) A. B.1 C. D.2 【考点】余弦定理. 【分析】由已知及余弦定理可求cosA,从而可求sinA的值,结合已知由三角形面积公式即可得解. 【解答】解:∵a2=b2+c2﹣bc, ∴由余弦定理可得:cosA===,又0<A<π, ∴可得A=60°,sinA=, ∵bc=4, ∴S△ABC=bcsinA==. 故选:C. 6.等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前n项和Sn=( ) A.n(n+1) B.n(n﹣1) C. D. 【考点】等差数列的性质. 【分析】由题意可得a42=(a4﹣4)(a4+8),解得a4可得a1,代入求和公式可得. 【解答】解:由题意可得a42=a2•a8, 即a42=(a4﹣4)(a4+8), 解得a4=8, ∴a1=a4﹣3×2=2, ∴Sn=na1+d, =2n+×2=n(n+1), 故选:A. 7.在△ABC中,b=,c=3,B=30°,则a=( ) A. B.2 C.或2 D.2 【考点】正弦定理. 【分析】由已知利用余弦定理可得a2﹣3a+6=0,进而即可解得a的值. 【解答】解:∵b=,c=3,B=30°, ∴由余弦定理b2=a2+c2﹣2accosB,可得:3=9+a2﹣3,整理可得:a2﹣3a+6=0, ∴解得:a=或2. 故选:C. 8.若{an}是等差数列,首项a1>0,a1007+a1008>0,a1007•a1008<0,则使前n项和Sn>0成立的最大自然数n是( ) A.2 012 B.2 013 C.2 014 D.2 015 【考点】数列的函数特性. 【分析】由已知条件推导出a1007>0,a1008<0,由此能求出使前n项和Sn>0成立的最大自然数n的值. 【解答】解:∵等差数列{an},首项a1>0,a1007+a1008>0,a1007•a1008<0, ∴a1007>0,a1008<0. 如若不然,a1007<0<a1008,则d>0, 而a1>0,得a1007=a1+1006d>0,矛盾,故不可能. ∴使前n项和Sn>0成立的最大自然数n为2014. 故选:C. 9.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( ) A.21 B.20 C.19 D.18 【考点】等差数列的前n项和. 【分析】写出前n项和的函数解析式,再求此式的最值是最直观的思路,但注意n取正整数这一条件. 【解答】解:设{an}的公差为d,由题意得 a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,① a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,② 由①②联立得a1=39,d=﹣2, ∴Sn=39n+×(﹣2)=﹣n2+40n=﹣(n﹣20)2+400, 故当n=20时,Sn达到最大值400. 故选:B. 10.根据下列情况,判断三角形解的情况,其中正确的是( ) A.a=8,b=16,A=30°,有两解 B.b=18,c=20,B=60°,有一解 C.a=5,c=2,A=90°,无解 D.a=30,b=25,A=150°,有一解 【考点】解三角形. 【分析】利用正弦定理分别对A,B,C,D选项进行验证. 【解答】解:A项中sinB=•sinA=1, ∴B=,故三角形一个解,A项说法错误. B项中sinC=sinB=, ∵0<C<π,故C有锐角和钝角两种解. C项中b==,故有解. D项中sinB=•sinA=,∵A=150°, ∴B一定为锐角,有一个解. 故选:D. 11.在等比数列{an}中,a2,a6是方程x2﹣34x+64=0的两根,则a4等于( ) A.8 B.﹣8 C.±8 D.以上都不对 【考点】函数的零点;等比数列的通项公式. 【分析】根据所给的等比数列的两项和方程根与系数的关系,求出a4的平方,根据条件中所给的三项都是偶数项,得出第四项是一个正数,得到结果. 【解答】解:∵a2,a6时方程x2﹣34x+64=0的两根,a2•a6=64, ∴a42=a2•a6=64 ∴a4=±8 ∵a4与a2,a6的符号相同, ∴a4=8 故选A. 12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( ) A.20(+)n mile/h B.20(﹣)n mile/h C.20(+)n mile/h D.20(﹣)n mile/h 【考点】解三角形的实际应用. 【分析】由题意知SM=20,∠SNM=105°,∠NMS=45°,∠MSN=30°,△MNS中利用正弦定理可得=,代入可求MN,进一步利用速度公式即可. 【解答】解:由题意知SM=20,∠NMS=45°, ∴SM与正东方向的夹角为75°,MN与正东方向的夹角为,60° ∴SNM=105° ∴∠MSN=30°, △MNS中利用正弦定理可得, =. MN==10()n mile, ∴货轮航行的速度v==20() n mile/h. 故选:B. 二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.三角形的两边分别为3cm,5cm,其所夹角的余弦为方程5x2﹣7x﹣6=0的根,则这个三角形的面积是 6 cm2. 【考点】正弦定理;同角三角函数间的基本关系. 【分析】解方程5x2﹣7x﹣6=0可得cosθ=﹣,利用同角三角函数的基本关系可得sinθ=,代入三角形的面积公式,运算求得结果. 【解答】解:解方程5x2﹣7x﹣6=0可得此方程的根为2或﹣,故夹角的余弦cosθ=﹣,∴sinθ=. 则这个三角形的面积是 =6. 故答案为:6. 14.已知数列{an}的前n项和为Sn,且Sn=3n2+2n﹣1,则数列{an}的通项公式an= . 【考点】数列递推式. 【分析】利用Sn+1﹣Sn可知an+1=6(n+1)﹣1,通过n=1可知首项,进而可得结论. 【解答】解:∵Sn=3n2+2n﹣1, ∴Sn+1=3(n+1)2+2(n+1)﹣1, 两式相减得:an+1=Sn+1﹣Sn =[3(n+1)2+2(n+1)﹣1]﹣(3n2+2n﹣1) =6n+5 =6(n+1)﹣1, 又∵a1=S1=3+2﹣1=4, ∴an=, 故答案为:. 15.设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C= . 【考点】余弦定理;正弦定理. 【分析】由3sinA=5sinB,根据正弦定理,可得3a=5b,再利用余弦定理,即可求得C. 【解答】解:∵3sinA=5sinB,∴由正弦定理,可得3a=5b, ∴a= ∵b+c=2a, ∴c= ∴cosC==﹣ ∵C∈(0,π) ∴C= 故答案为: 16.设等差数列{an}的前n项和为Sn,若a5=5a3,则= 9 . 【考点】等差数列的性质. 【分析】根据等差数列的等差中项的性质可知S9=9a5,S5=5a3,根据a5=5a3,进而可得则的值. 【解答】解:∵{an}为等差数列, S9=a1+a2+…+a9=9a5,S5=a1+a2+…+a5=5a3, ∴ 故答案为9 三、解答题(本大题共6个小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤) 17.已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cosB= (Ⅰ)若b=4,求sinA的值; (Ⅱ) 若△ABC的面积S△ABC=4求b,c的值. 【考点】正弦定理;余弦定理. 【分析】(Ⅰ)先求出sinB=,再利用正弦定理求sinA的值; (Ⅱ)由△ABC的面积S△ABC=4求c的值,利用余弦定理求b的值. 【解答】解:(Ⅰ)∵cosB= ∴sinB=, ∵a=2,b=4, ∴sinA===; (Ⅱ)S△ABC=4=×2c×,∴c=5, ∴b==. 18.已知等差数列{an}中,a10=30,a20=50. (1)求通项公式; (2)若Sn=242,求项数n. 【考点】等差数列的前n项和;等差数列的通项公式. 【分析】(1)由a10=a1+9d=30,a20=a1+19d=50,求出首项和公差,即得等差数列{an} 的通项公式. (2)由Sn =242,可得 242=12n+n(n﹣1)•2,解方程求得项数n 的值. 【解答】解:(1)a10=a1+9d=30,a20=a1+19d=50, 解得 a1=12,d=2. ∴an=a1 +(n﹣1)d=2n+10.… (2)∵Sn =na1+n(n﹣1)d, ∴242=12n+n(n﹣1)•2,解得 n=11,或 n=﹣22 (舍去), 故取n=11. … 19.在△ABC中,已知内角A=,边BC=2,设内角B=x,周长为y (1)求函数y=f(x)的解析式和定义域; (2)求y的最大值. 【考点】在实际问题中建立三角函数模型;三角函数的最值. 【分析】(1)由内角A=,边BC=2,设内角B=x,周长为y,我们结合三角形的性质,△ABC的内角和A+B+C=π,△ABC的周长y=AB+BC+AC,我们可以结合正弦定理求出函数的解析式,及自变量的取值范围. (2)要求三角函数的最值,我们要利用辅助角公式,将函数的解析式,化为正弦型函数的形式,再根据正弦型函数的最值的求法进行求解. 【解答】解:(1)△ABC的内角和A+B+C=π, 由得 . 应用正弦定理,知 , . 因为y=AB+BC+AC, 所以, (2)∵ =, 所以,当, 即时, y取得最大值. 20.设各项均为正数的数列{an}的前n项和为Sn,且Sn满足﹣(n2+n﹣3)Sn﹣3(n2+n)=0,n∈N*. (1)求a1的值; (2)求数列{an}的通项公式. 【考点】数列递推式. 【分析】(1)本题可以用n=1代入题中条件,利用S1=a1求出a1的值; (2)把已知递推式因式分解,求出Sn,由an=Sn﹣Sn﹣1(n≥2)求得答案. 【解答】解:(1)由﹣(n2+n﹣3)Sn﹣3(n2+n)=0,得 ,即, 解得:a1=﹣3(舍)或a1=2; (2)由﹣(n2+n﹣3)Sn﹣3(n2+n)=0, 得(Sn+3)()=0, 即. 当n=1时,a1=2. 当n≥2时,. 验证n=1时上式成立, ∴an=2n. 21.在△ABC中,角A、B、C的对边分别为a、b、c,面积为S,已知acos2+ccos2=b (1)求证:a、b、c成等差数列; (2)若B=,S=4 求b. 【考点】余弦定理;正弦定理. 【分析】(1)已知等式利用正弦定理化简,再利用二倍角的余弦函数公式及两角和与差的正弦函数公式变形,整理后再利用正弦定理化简,利用等差数列的性质判断即可得证; (2)利用三角形面积公式列出关系式,把sinB与已知面积代入求出ac的值,利用余弦定理列出关系式,整理得出b的值即可. 【解答】解:(1)由正弦定理得:sinAcos2+sinCcos2=sinB, 即sinA•+sinC•=sinB, ∴sinA+sinC+sinAcosC+cosAsinC=3sinB,即sinA+sinC+sin(A+C)=3sinB, ∵sin(A+C)=sinB, ∴sinA+sinC=2sinB, 由正弦定理化简得:a+c=2b, ∴a,b,c成等差数列; (2)∵S=acsinB=ac=4, ∴ac=16, 又b2=a2+c2﹣2accosB=a2+c2﹣ac=(a+c)2﹣3ac, 由(1)得:a+c=2b, ∴b2=4b2﹣48,即b2=16, 解得:b=4. 22.已知数列{an},an∈N*,前n项和Sn=(an+2)2. (1)求证:{an}是等差数列; (2)若bn=an﹣30,求数列{bn}的前n项和的最小值. 【考点】等差关系的确定;数列的求和. 【分析】本题考查数列的通项与其前n项和的关系、等差数列的证明、数列的求和等综合性问题. (1)根据an+1=Sn+1﹣Sn及前n项和Sn=(an+2)2,可以得到(an+1+an)(an+1﹣an﹣4)=0,从而问题得证. (2)由(1)可得数列{an}的通项公式,进而由bn=an﹣30得到数列{bn}的通项公式,然后可求数列{bn}的前n项和,再由此求其最小值,最小值有两种求法,其一是转化为二次函数的最值,其二是找出正负转折的项. 【解答】解:(1)证明:∵an+1 =Sn+1﹣Sn =(an+1+2)2﹣(an+2)2, ∴8an+1=(an+1+2)2﹣(an+2)2, ∴(an+1﹣2)2﹣(an+2)2=0,(an+1+an)(an+1﹣an﹣4)=0. ∵an∈N*,∴an+1+an≠0, ∴an+1﹣an﹣4=0. 即an+1﹣an=4,∴数列{an}是等差数列. (2)由(1)知a1=S1=(a1+2)2,解得a1=2.∴an=4n﹣2, bn=an﹣30=2n﹣31,(以下用两种方法求解) 法一: 由bn=2n﹣31可得:首项b1=﹣29,公差d=2 ∴数列{bn}的前n项和sn=n2﹣30n=(n﹣15)2﹣225 ∴当n=15时,sn=﹣225为最小; 法二: 由得 ≤n≤.∵n∈N*,∴n=15, ∴{an}前15项为负值,以后各项均为正值. ∴S15最小.又b1=﹣29, ∴S15==﹣225查看更多