2021届课标版高考理科数学大一轮复习课件：11-4　抽样方法与总体分布的估计（讲解部分）

2021届课标版高考理科数学大一轮复习课件：11-4　抽样方法与总体分布的估计（讲解部分）

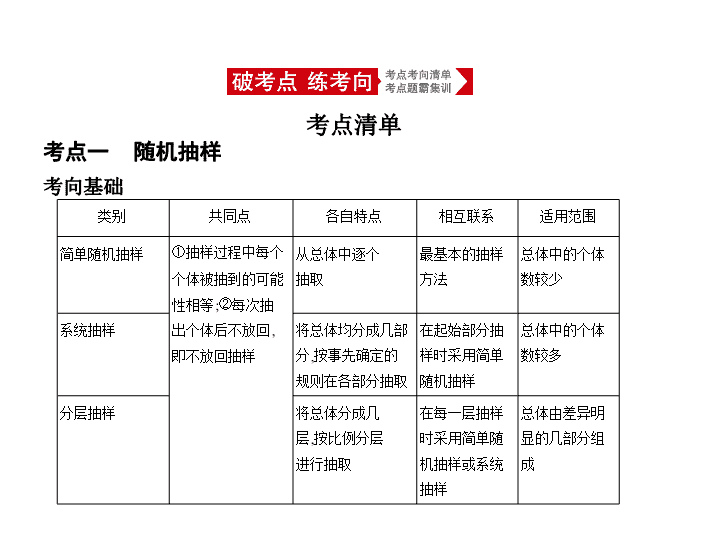
11.4 　抽样方法与总体分布的估计 高考理数 考点一    随机抽样 考点清单 考向基础 类别 共同点 各自特点 相互联系 适用范围 简单随机抽样 ①抽样过程中每个个体被抽到的可能性相等;②每次抽出个体后不放回,即不放回抽样 从总体中逐个 抽取 最基本的抽样 方法 总体中的个体 数较少 系统抽样 将总体均分成几部分,按事先确定的规则在各部分抽取 在起始部分抽 样时采用简单 随机抽样 总体中的个体 数较多 分层抽样 将总体分成几 层,按比例分层 进行抽取 在每一层抽样 时采用简单随 机抽样或系统 抽样 总体由差异明 显的几部分组 成 考向突破 考向    三种抽样方法的运用 例     (2020届四川9月联合诊断,3)某运动队由足球运动员18人,篮球运动员 12人,乒乓球运动员6人组成(每人只参加一项),现从这些运动员中抽取一 个容量为 n 的样本,若分别采用系统抽样法和分层抽样法,都不用删除个体, 那么样本容量 n 的最小值为   (　　) A.6　　　　    B.12　　　　    C.18　　　　    D.24 解析 　本题考查了分层抽样和系统抽样的应用问题,解题时应对两种抽样 方法进行分析和讨论,以便求出样本容量. 由题意知,总体容量为36,当样本容量为 n 时,系统抽样的抽样间隔为   ,分 层抽样的抽样比为   ,则采用分层抽样抽取的足球运动员人数为   × 18=   ,篮球运动员人数为   × 12=   ,乒乓球运动员人数为   × 6=   ,可知 n 是6的 整数倍,故 n 的最小值为6. 答案     A 考点二    用样本估计总体 考向基础 1.频率分布表与频率分布直方图 频率分布表与频率分布直方图的绘制步骤如下: (1) 求极差 ,即求一组数据中最大值与最小值的差; (2) 决定组距与组数; (3) 将数据分组; (4) 列频率分布表 ,落在各小组内的数据的个数叫做频数,每小组的频数与 样本容量的比值叫做这一小组的频率,计算各小组的频率,列出频率分布表; (5) 画频率分布直方图 ,依据频率分布表画出频率分布直方图,其中纵坐标 (小长方形的高)表示频率与组距的比值,其相应组距上的频率等于该组上 的小长方形的面积,即每个小长方形的面积=组距 ×   =频率. 各个小长方形面积的总和等于1. 2.频率分布折线图和总体密度曲线 (1)频率分布折线图:连接频率分布直方图中各小长方形上端的中点,就得 到频率分布折线图. (2)总体密度曲线:随着样本容量的增加,作频率分布直方图时所分的组数 增加,组距减小,相应的频率分布折线图会越来越接近于一条光滑曲线,统 计中称这条光滑曲线为总体密度曲线. 3.茎叶图 茎叶图是统计中用来表示数据的一种图,茎是指中间的一列数,叶就是从茎 的旁边生长出来的数. 数字特征 样本数据 频率分布直方图 众数 出现次数最多的数据 取最高的小长方形底边中点的横坐标 中位数 将数据按大小依次排列,处在最中间位置的一个数据(或最中间两个数据的平均数) 把频率分布直方图划分为左右两个面积相等的部分,分界线与 x 轴交点的横坐标 平均数 样本数据的算术平均数 每个小长方形的面积乘小长方形底边中点的横坐标之和 4.用样本的数字特征估计总体的数字特征 　　方差和标准差 方差和标准差反映了数据波动程度的大小. 方差: s 2 = ； 标准差: s = . 注意: 方差和标准差描述了一组数据与平均数的离散程度,反映了一组数据 相对于平均数的波动情况,标准差和方差越大,说明这组数据的波动性越大. 考向突破 考向一    统计图表的应用 例1     (2019安徽六安毛坦厂中学3月月考,3)某位教师2017年的家庭总收入 为80 000元,各种用途占比统计如下面的折线图.2018年收入的各种用途占 比统计如下面的条形图,已知2018年的就医费用比2017年增加了4 750元, 则该教师2018年的家庭总收入为   (　　)   A.100 000元　　　　    B.95 000元 C.90 000元　　　　    D.85 000元 解析 　由已知得,2017年的就医费用为80 000 × 10%=8 000元,故2018年的就 医费用为12 750元,所以该教师2018年的家庭总收入为   =85 000(元). 故选D. 答案     D 考向二    用样本的数字特征估计总体的数字特征 例2     (2019河南名校联盟尖子生第六次联合调研,5)某外卖企业抽取了阿 朱、阿紫两位员工今年3月某10天日派送外卖量的数据(单位:件),如茎叶 图所示.针对这10天的数据,下面说法错误的是   (　　)   A.阿朱的日派送外卖量的众数为76 B.阿紫的日派送外卖量的中位数为77 C.阿朱的日派送外卖量的中位数为76.5 D.阿紫的日派送外卖量更稳定 解析 　阿朱的日派送外卖量中,只有76出现了2次,其他数只出现了1次,故 众数为76,A中的说法正确;计算可得阿朱、阿紫的日派送外卖量的中位数 分别为76.5、77,B、C中的说法正确;阿朱日派送外卖量波动较小,更稳定, D中的说法错误. 答案     D 方法1      抽样方法的应用 1.系统抽样的最基本特征是“等距性”.一般地,每组内所抽取的号码依据 第一组抽取的号码和组距确定.每组抽取的号码依次构成一个以第一组抽 取的号码 m 为首项、组距 d 为公差的等差数列{ a n },第 k 组抽取的号码为 a k = m +( k -1) d . 2.分层抽样的关键是根据样本特征的差异进行分层,实质是等比例抽样,抽 样比=   =   . 方法技巧 例1 　(1)(2019河南部分省示范性高中1月份联考,7)某学校为落实学生掌 握社会主义核心价值观的情况,用系统抽样的方法从全校2 400名学生中抽 取30人进行调查.现将2 400名学生随机地从1~2 400编号,按编号顺序平均 分成30组(1~80号,81~160号, …… ,2 321~2 400号),若第3组与第4组抽出的 号码之和为432,则第6组抽到的号码是   (　　) A.416　　　　    B.432　　　　    C.448　　　　    D.464 (2)(2018安徽安庆一中、山西太原五中等五省六校期末联考,3)某中学有 高中生960人,初中生480人,为了了解学生的身体状况,采用分层抽样的方 法,从该校学生中抽取容量为 n 的样本,其中高中生有24人,那么 n 等于   (    　) A.12　　　　    B.18　　　　    C.24　　　　    D.36 解析 　(1)设第 n 组抽到的号码是 a n ,则{ a n }构成以80为公差的等差数列, 所以 a 3 = a 1 +80 × 2=160+ a 1 , a 4 = a 1 +80 × 3=240+ a 1 ,则有 a 3 + a 4 =2 a 1 +400=432, 解得 a 1 =16,所以 a 6 =16+80 × 5=416.故选A. (2)根据分层抽样方法知   =   ,解得 n =36. 答案　 (1)A　(2)D 方法2      频率分布直方图的应用 1.绘制频率分布直方图时需注意: (1)频率分布直方图中的纵轴表示   ,而不是频率; (2)频率分布直方图中各小长方形的高之比就是相应各组的频率之比; (3)频率分布直方图中各个小长方形的面积是相应各组的频率,所有的小长 方形的面积之和等于1,即频率之和为1. 2.由频率分布直方图进行相关计算时,需掌握下列关系式: (1)   × 组距=频率; (2)   =频率,此关系式的变形为   =样本容量,样本容量 × 频率=频 数. 例2     (2020届四川联合诊断,17)我国是世界上严重缺水的国家,某市政府 为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理 的月用水量标准 x (吨),一位居民的月用水量不超过 x 的部分按平价收费,超 出 x 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100 位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1), … ,[4,4.5]分 成9组,制成了如图所示的频率分布直方图. (1)求直方图中 a 的值; (2)设该市有30万居民,估计全市居民中 月均用水量不低于3吨的人数,并说明理由; (3)若该市政府希望使85%的居民每月的用 水量不超过标准 x (吨),估计 x 的值,并说明理由. 解析 　(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08 × 0.5=0.04, 同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]中的频率分别为0.08,0.20, 0.26,0.06,0.04,0.02. 由0.04+0.08+0.5 × a +0.20+0.26+0.5 × a +0.06+0.04+0.02=1,解得 a =0.30. (2)由(1)知,100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12. 由以上样本的频率分布,可以估计全市30万居民中月均用水量不低于3吨 的人数为300 000 × 0.12=36 000. (3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85, 而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,所以2.5 ≤ x <3. 由0.3 × ( x -2.5)=0.85-0.73,解得 x =2.9. 所以,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准. 方法3      样本的数字特征及其应用 1.平均数、中位数、众数与方差、标准差都是重要的数字特征,利用它们 可对总体进行一种简明的描述,它们所反映的情况有着重要的实际意义,平 均数、中位数、众数可描述总体的集中趋势,方差和标准差可描述波动大小. 2.有关平均数、方差的一些结论: (1)若数据 x 1 , x 2 , … , x n 的平均数为   ,那么 mx 1 + a , mx 2 + a , mx 3 + a , … , mx n + a 的平均 数是 m   + a . (2)设数据 x 1 , x 2 , … , x n 的方差为 s 2 ,则 ① s 2 =   [( x 1 -   ) 2 +( x 2 -   ) 2 + … +( x n -   ) 2 ]; ②数据 x 1 + a , x 2 + a , … , x n + a 的方差也为 s 2 ; ③数据 ax 1 , ax 2 , … , ax n 的方差为 a 2 s 2 . 例3     (2018河南新乡一模,19)为了了解甲、乙两个工厂生产的轮胎的宽度 是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记 录下来并绘制出如下的折线图:     (1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值; (2)若轮胎的宽度在[194,196]内,则称这个轮胎是标准轮胎.试比较甲、乙 两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的 标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对 更好. 解析　 (1)甲厂10个轮胎宽度的平均值:   =   × (195+194+196+193+194+197+196+195+193+197)=195(mm), 乙厂10个轮胎宽度的平均值:   =   × (195+196+193+192+195+194+195+ 192+195+193)=194(mm). (2)甲厂10个轮胎中宽度在[194,196]内的数据为195,194,196,194,196,195, 平均数:   =   × (195+194+196+194+196+195)=195, 方差:   =   × [(195-195) 2 +(194-195) 2 +(196-195) 2 +(194-195) 2 +(196-195) 2 +(195- 195) 2 ]=   , 乙厂10个轮胎中宽度在[194,196]内的数据为195,196,195,194,195,195, 平均数:   =   × (195+196+195+194+195+195)=195, 方差:   =   × [(195-195) 2 +(196-195) 2 +(195-195) 2 +(194-195) 2 +(195-195) 2 +(195- 195) 2 ]=   , ∵两厂标准轮胎宽度的平均数相等,但乙厂的方差更小, ∴乙厂的轮胎相对更好.