2015年高考数学（文科）真题分类汇编N单元 选修4系列

2015年高考数学（文科）真题分类汇编N单元 选修4系列

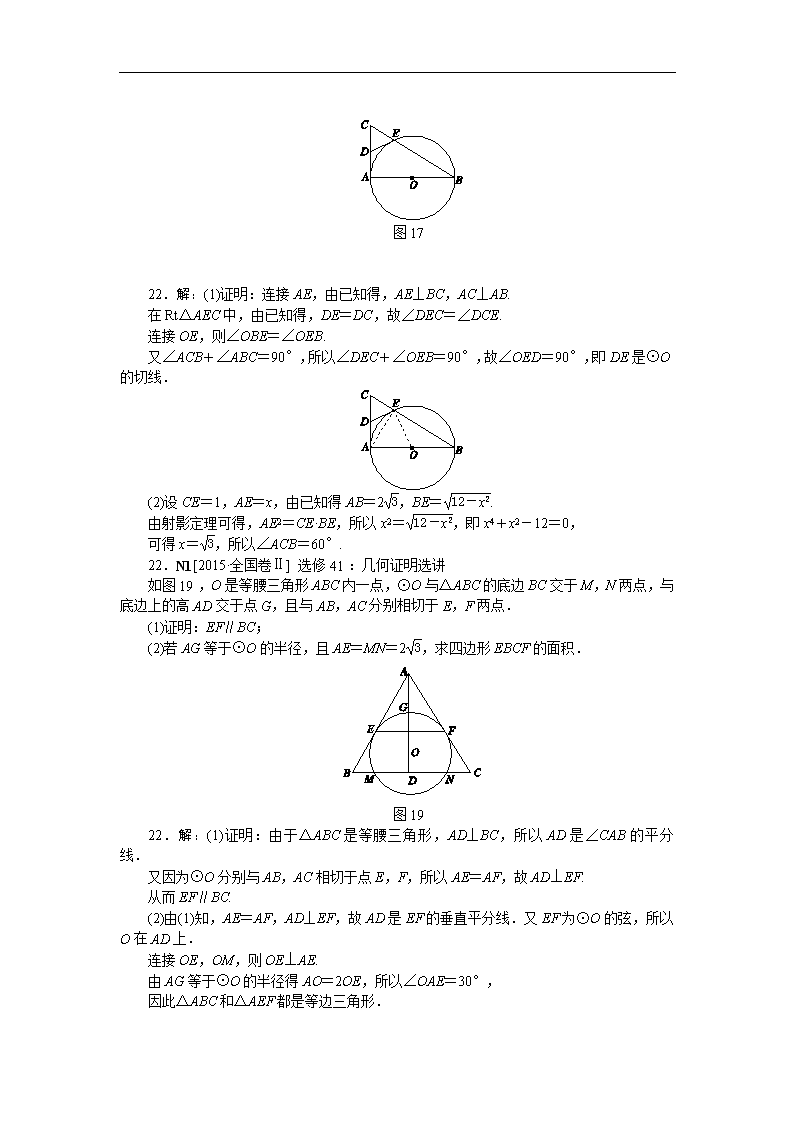
‎ 数 学 N单元 选修4系列 ‎ N1 选修4-1 几何证明选讲 ‎ 15．N1[2015·广东卷] (几何证明选讲选做题)如图11，AB为圆O的直径，E为AB延长线上一点，过E作圆O的切线，切点为C，过A作直线EC的垂线，垂足为D.若AB＝4，CE＝2，则AD＝________.‎ 图11‎ ‎15．3　[解析] 连接OC，则OC⊥DE，∴OC∥AD，∴＝.由切割线定理得CE2＝BE·AE，∴BE(BE＋4)＝12，解得BE＝2，∴AD＝＝＝3.‎ ‎22．N1[2015·全国卷Ⅰ] 选修41：几何证明选讲 如图17，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E.‎ ‎(1)若D为AC的中点，证明：DE是⊙O的切线；‎ ‎(2)若OA＝CE，求∠ACB的大小．‎ 图17‎ ‎22．解：(1)证明：连接AE，由已知得，AE⊥BC，AC⊥AB.‎ 在Rt△AEC中，由已知得，DE＝DC，故∠DEC＝∠DCE.‎ 连接OE，则∠OBE＝∠OEB.‎ 又∠ACB＋∠ABC＝90°，所以∠DEC＋∠OEB＝90°，故∠OED＝90°，即DE是⊙O的切线．‎ ‎(2)设CE＝1，AE＝x，由已知得AB＝2，BE＝.‎ 由射影定理可得，AE2＝CE·BE，所以x2＝，即x4＋x2－12＝0，‎ 可得x＝，所以∠ACB＝60°.‎ ‎22．N1[2015·全国卷Ⅱ] 选修41：几何证明选讲 如图19，O是等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．‎ ‎(1)证明：EF∥BC；‎ ‎(2)若AG等于⊙O的半径，且AE＝MN＝2，求四边形EBCF的面积．‎ 图19‎ ‎22．解：(1)证明：由于△ABC是等腰三角形，AD⊥BC，所以AD是∠CAB的平分线．‎ 又因为⊙O分别与AB，AC相切于点E，F，所以AE＝AF，故AD⊥EF.‎ 从而EF∥BC.‎ ‎(2)由(1)知，AE＝AF，AD⊥EF，故AD是EF的垂直平分线．又EF为⊙O的弦，所以O在AD上．‎ 连接OE，OM，则OE⊥AE.‎ 由AG等于⊙O的半径得AO＝2OE，所以∠OAE＝30°，‎ 因此△ABC和△AEF都是等边三角形．‎ 因为AE＝2，所以AO＝4，OE＝2.‎ 因为OM＝OE＝2，DM＝MN＝，所以OD＝1.于是AD＝5，AB＝.‎ 所以四边形EBCF的面积为×2×－×(2)2×＝.‎ ‎22．N1[2015·陕西卷] 选修41：几何证明选讲 如图17，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C.‎ ‎(1)证明：∠CBD＝∠DBA；‎ ‎(2)若AD＝3DC，BC＝，求⊙O的直径．‎ 图17‎ ‎22．解：(1)证明：因为DE为⊙O的直径，‎ 所以∠BED＋∠EDB＝90°.‎ 又BC⊥DE，所以∠CBD＋∠EDB＝90°，‎ 从而∠CBD＝∠BED.‎ 又AB切⊙O于点B，‎ 得∠DBA＝∠BED，‎ 所以∠CBD＝∠DBA.‎ ‎(2)由(1)知BD平分∠CBA，‎ 则＝＝3.‎ 又BC＝，从而AB＝3，‎ 所以AC＝＝4，‎ 所以AD＝3.‎ 由切割线定理得AB2＝AD·AE，‎ 即AE＝＝6，‎ 故DE＝AE－AD＝3，‎ 即⊙O的直径为3.‎ ‎6．N1[2015·天津卷] 如图12，在圆O中，M，N是弦AB的三等分点，弦CD，CE分别经过点M，N，若CM＝2，MD＝4，CN＝3，则线段NE的长为(　　)‎ 图12‎ A. B．3‎ C. D. ‎6．A　[解析] 根据相交弦定理知，CM·MD＝AM·MB，CN·NE＝AN·NB.又因为M，N ‎ 是弦AB 的三等分点，所以CM·MD＝CN·NE，即2×4＝3×NE，所以NE＝.‎ N2 选修4-2 矩阵 N3 选修4-4 参数与参数方程 ‎23．N3[2015·全国卷Ⅰ] 选修44：坐标系与参数方程 在直角坐标系xOy中，直线C1：x＝－2，圆C2：(x－1)2＋(y－2)2＝1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．‎ ‎(1)求C1，C2的极坐标方程；‎ ‎(2)若直线C3的极坐标方程为θ＝(ρ∈R)，设C2与C3的交点为M，N，求△C2MN的面积．‎ ‎23．解：(1)因为x＝ρcos θ，y＝ρsin θ，所以C1的极坐标方程为ρcos θ＝－2，C2的极坐标方程为ρ2－2ρcos θ－4ρsin θ＋4＝0.‎ ‎(2)将θ＝代入ρ2－2ρcos θ－4ρsin θ＋4＝0，得ρ2－3ρ＋4＝0，解得ρ1＝2，ρ2＝，故ρ1－ρ2＝，即|MN|＝.‎ 由于圆C2的半径为1，所以△C2MN的面积为.‎ ‎23．N3[2015·全国卷Ⅱ] 选修44：坐标系与参数方程 在直角坐标系xOy中，曲线C1：(t为参数，t≠0)，其中0≤α<π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sin θ，C3：ρ＝2cos θ.‎ ‎(1)求C2与C3交点的直角坐标；‎ ‎(2)若C1与C2相交于点A，C1与C3相交于点B，求|AB|最大值．‎ ‎23．解：(1)曲线C2的直角坐标方程为x2＋y2－2y＝0，曲线C3的直角坐标方程为x2＋y2－2x＝0.‎ 联立解得或 所以C2与C3交点的直角坐标为(0，0)和，.‎ ‎(2)曲线C1的极坐标方程为θ＝α(ρ∈R，ρ≠0)，其中0≤α<π.‎ 因此A的极坐标为(2sin α，α)，B的极坐标为(2cos α，α)．‎ 所以|AB|＝|2sin α－2cos α|＝4sinα－.‎ 当α＝时，|AB|取得最大值，最大值为4.‎ ‎12．N3[2015·湖南卷] 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．若曲线C的极坐标方程为ρ＝2sin θ，则曲线C的直角坐标方程为________．‎ ‎12．x2＋y2－2y＝0　[解析] 将曲线C的极坐标方程ρ＝2sin θ两边同乘一个ρ，得ρ2‎ ‎＝2ρsin θ，即x2＋y2＝2y，故曲线C的直角坐标方程为x2＋y2－2y＝0.‎ ‎23．N3[2015·陕西卷] 选修44：坐标系与参数方程 在直角坐标系xOy中，直线l的参数方程为(t为参数)．以原点为极点，x轴正半轴为极轴建立极坐标系，⊙C的极坐标方程为ρ＝2sin θ.‎ ‎(1)写出⊙C的直角坐标方程；‎ ‎(2)P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．‎ ‎23．解：(1)由ρ＝2sin θ，得ρ2＝2ρsin θ，‎ 从而有x2＋y2＝2y，所以x2＋(y－)2＝3.‎ ‎(2)设P3＋t，t，又C(0，)，‎ 则|PC|＝＝，‎ 故当t＝0时，|PC|取得最小值，‎ 此时，P点的直角坐标为(3，0)．‎ ‎14．N3[2015·广东卷] (坐标系与参数方程选做题)在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C1的极坐标方程为ρ(cos θ＋sin θ)＝－2，曲线C2的参数方程为(t为参数)，则C1与C2交点的直角坐标为________．‎ ‎14．(2，－4)　[解析] 曲线C1的直角坐标方程为x＋y＝－2，曲线C2的普通方程为y2＝8x，由得所以C1与C2交点的直角坐标为(2，－4)．‎ N4 选修4-5 不等式选讲 ‎24．N4[2015·全国卷Ⅰ] 选修45：不等式选讲 已知函数f(x)＝|x＋1|－2|x－a|，a>0.‎ ‎(1)当a＝1时，求不等式f(x)>1的解集；‎ ‎(2)若f(x)的图像与x轴围成的三角形面积大于6，求a的取值范围．‎ ‎24．解：(1)当a＝1时，f(x)>1化为|x＋1|－2|x－1|－1>0.‎ 当x≤－1时，不等式化为x－4>0，无解；‎ 当－10，解得0，解得1≤x<2.‎ 所以f(x)>1的解集为.‎ ‎(2)由题设可得，f(x)＝ 所以函数f(x)的图像与x轴围成的三角形的三个顶点分别为A，B(‎2a＋1，0)，C(a，a＋1)，△ABC的面积为(a＋1)2.‎ 由题设得(a＋1)2>6，故a>2，‎ 所以a的取值范围为(2，＋∞)．‎ ‎24．N4[2015·全国卷Ⅱ] 选修45：不等式选讲 设a，b，c，d均为正数，且a＋b＝c＋d.证明：‎ ‎(1)若ab>cd，则＋>＋；‎ ‎(2)＋>＋是|a－b|<|c－d|的充要条件．‎ ‎24．证明：(1)因为(＋)2＝a＋b＋2，(＋)2＝c＋d＋2，由题设a＋b＝c＋d，ab>cd得(＋)2>(＋)2.‎ 因此＋>＋.‎ ‎(2)(i)若|a－b|<|c－d|，则(a－b)2<(c－d)2，即 ‎(a＋b)2－4ab<(c＋d)2－4cd.‎ 因为a＋b＝c＋d，所以ab>cd.‎ 由(1)得＋>＋.‎ ‎(ii)若＋>＋，则(＋)2>(＋)2，即a＋b＋2>c＋d＋2.‎ 因为a＋b＝c＋d，所以ab>cd.‎ 于是(a－b)2＝(a＋b)2－4ab<(c＋d)2－4cd＝(c－d)2.‎ 因此|a－b|<|c－d|.‎ 综上，＋>＋是|a－b|<|c－d|的充要条件．‎ ‎24．N4[2015·陕西卷] 选修45：不等式选讲 已知关于x的不等式|x＋a|

查看更多