- 2021-06-10 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
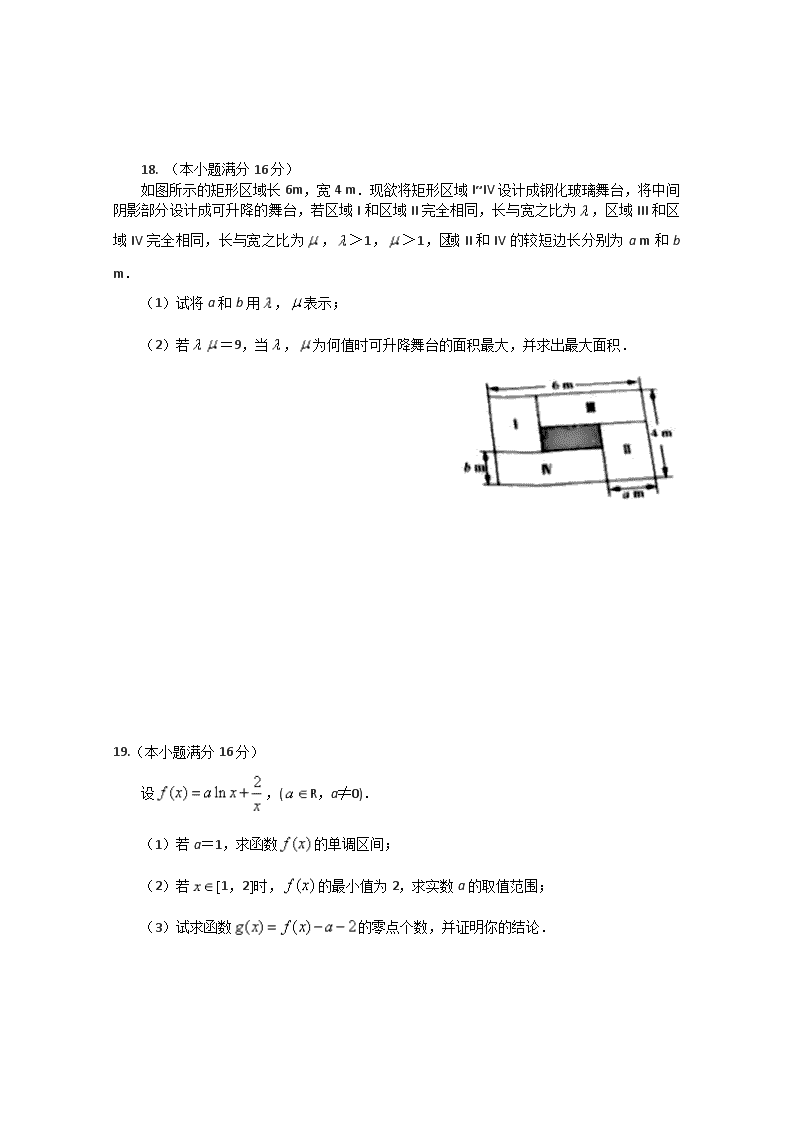
江苏省金陵中学2020届高三下学期6月测试数学试题
2019-2020学年度第二学期高三考前训练 数 学 第I卷(必做题,共160分) 一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.) 1.已知集合A={0,1,2,3},B={﹣1,0,3},则AB= . 2.已知复数z满足,其中i为虚数单位,则复数z的模为 . 3.已知双曲线的一条渐近线方程为,则该双曲线的离心率e=_______ 4.某工生产A,B,C三种不同型号的产品,产量之比为1:2:3.现用分层抽样的方法抽取1个容量为n的样本,若样本中A种型号的产品有8件,则样本容量n的值为 . 5.根据如图所示的伪代码,可知输出S的值为 6.已知函数¦(x)=sinx+cosx的定义域为[a,b],值域为[ ―1, ],则b―a的取值范围是 7.下列四个命题: “”的否定; )“若”的否命题; 在中,“”是“”的充分不必要条件; “函数为奇函数”的充要条件是“”. 其中真命题的序号是____________________(真命题的序号都填上) 8..在面积为2的中,E,F分别是AB,AC的中点,点P在直线EF上,则的最小值是______________ 9.设关于x的不等式,只有有限个整数解,且0是其中一个解,则全部不等式的整数解的和为 10.如图,△ABC为等边三角形,分别延长BA, CB, AC到点D, E,F,使得AD= BE=CF .若=2,且DE=,则.的值是 11、已知函数f(x)= ++2bx+c在区间(0,1)内取极大值,在区间(1,2)内取极小值,则z=(a+3)2+b2的取值范围为 12.公园里设置了一些石凳供游客休息,这些石凳是经过正方体各棱的中点截去8个一样的四面体得到的( 如图所示).设石凳的体积为以,正方体的体积为,的值是 . 13.已知函数f(x)= ,f(x)=x 的根从小到大构成数列{an},则a2012= 14.已知函数,,记函数,若在(0,)上恰有2个不同的零点,则实数a的取值范围是 . 二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分) 已知动点在角的终边上. (1)若,求实数t的值; (2)记,试用t将S表示出来. 16.(本小题满分14分) 如图,在正三棱柱ABC—A1B1C1中,点D是BC的中点. (1)求证:A1C∥平面AB1D; (2)设M为棱CC1的中点,且满足BB1=BC,求证:平面AB1D⊥平面ABM. 17.(本小题满分14分) 在三角形ABC中,已知tanC=,cosB=. (1)求tanA的值; (2)若△ABC的面积为,求边BC的长. 18. (本小题满分16分) 如图所示的矩形区域长6m,宽4 m.现欲将矩形区域I~IV设计成钢化玻璃舞台,将中间阴影部分设计成可升降的舞台,若区域I和区域II完全相同,长与宽之比为,区域III和区域IV完全相同,长与宽之比为,>1,>1,区域II和IV的较短边长分别为a m和b m. (1)试将a和b用,表示; (2)若=9,当,为何值时可升降舞台的面积最大,并求出最大面积. 19.(本小题满分16分) 设,(R,a≠0). (1)若a=1,求函数的单调区间; (2)若[1,2]时,的最小值为2,求实数a的取值范围; (3)试求函数的零点个数,并证明你的结论. 20. (本小题满分16分) 设数列的前n项和为, (1)求证:数列是等比数列; (2)若,是否存在q的某些取值,使数列中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。 (3)若,是否存在,使数列中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。 2019-2020学年度第二学期高三考前训练 数 学(附加) 第II卷(附加题,共40分) 21.【选做题】本题包括A,B,C三小题,请选定其中两题作答,每小题10分共计20分,解答时应写出文字说明,证明过程或演算步骤. A.选修4—2:矩阵与变换 已知曲线,先将曲线C作关于x轴的反射变换,再将所得图形绕原点顺时针旋转90°. (1)求连续两次变换所对应的变换矩阵M; (2)求曲线C在TM作用下得到的曲线C′的方程. B.选修4—4:坐标系与参数方程 在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数).椭圆C的参数方程为(为参数),设直线l与椭圆C交于A、B两点,求线段AB的长. 【必做题】第22题、第23题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤. 22.(本小题满分10分) 支付宝作为一款移动支付工具,在日常生活中起到了重要的作用. (1)通过现场调查12位市民得知,其中有10人使用支付宝.现从这12位市民中随机抽取3人,求至少抽到2位使用支付宝的市民的概率; (2)为了鼓励市民使用支付宝,支付宝推出了“奖励金”活动,每使用支付宝支付一次,分别有,,的概率获得0.1,0.2,0.3元奖励金,每次支付获得的奖励金情况互不影响.若某位市民在一天内使用了2次支付宝,记X为这一天他获得的奖励金数,求X的概率分布和数学期望. 23.(本小题满分10分) 在平面直角坐标系xOy中,如图,已知抛物线上一点M(4,a)到抛物线焦点F的距离为5. (1)求抛物线的方程及实数a的值; (2)过点M作抛物线的两条弦MA,MB,若MA,MB的倾斜角分别为,,且+=135°,求证:直线AB过定点,并求出这个定点的坐标.查看更多