- 2021-06-10 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-2课件1_7_1 定积分在几何中的应用
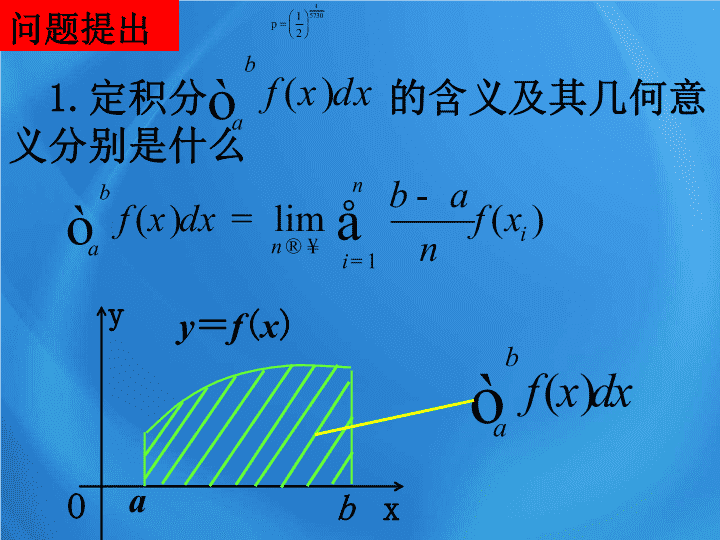
1.7 定积分的简单应用 1.7.1 定积分在几何中的应用 问题提出 1. 定积分 的含义及 其几何意义分别是什么 x y a b y = f ( x ) O 2. 微积分基本定理是什么? 如果 f ( x ) 是区间 [ a , b ] 上的连续函数, 并且 ,则 . 3. 用定积分可以表示曲边梯形的面积,微积分基本定理为定积分的计算提供了一种有效的方法,二者强强联合,可以解决平面几何中曲边图形的面积问题 . 定积分在几 何中的应用 探究(一): 曲线 y 2 = x 与 y = x 2 所围成图 形的面积 思考 1 : 曲线 y 2 = x 与 y = x 2 所围成的图形是什么?其交点坐标是什么? 1 1 x y O y 2 = x y = x 2 (0,0) (1,1) 思考 2 : 如何将该图形的面积转化为曲边梯形的面积? x y O 1 1 A B C D y 2 = x y = x 2 S = S 曲边梯形 OABC - S 曲边梯形 OADC. 思考 3 : 该图形的面积用定积分怎样表示? x y O 1 1 A B C D y 2 = x y = x 2 思考 4 : 利用微积分基本定理计算,该图形的面积等于多少? x y O 1 1 A B C D y 2 = x y = x 2 探究(二): 直线 y = x - 4 与曲线 及 x 轴所围成图形的面积 思考 1 : 直线 y = x - 4 与曲线 及 x 轴所围成的图形是什么?各顶点的坐标是什么? 8 4 4 x y O y = x - 4 (8,4) (0,0) (4,0) x y O 4 8 y = x - 4 4 A B C D 思考 2 : 如何将该图形的面积转化为曲边梯形的面积? S = S 曲边梯形 OABC - S 三角形 ABD. 思考 3 : 该图形的面积用定积分怎样表示? x y O 4 8 y = x - 4 4 A B C D 思考 4 : 利用微积分基本定理计算,该图形的面积等于多少? x y O 4 8 y = x - 4 4 A B C D 理论迁移 例 1 计算由直线 y = 2 - x , 和曲线 所围成的平面图形的面积 . x y O 3 2 y = 2 - x 1 A B 1 - 1 例 2 如图,直线 y = k x 将抛物线 y = x - x 2 与 x 轴所围成的平面图形分成 面积相等的两部分,求实数 k 的值 . x y O y = kx y = x - x 2 1 1 - k 小结作业 1. 定积分在几何中的应用,主要用于求平面曲边图形的面积 . 解题时,一般先要画出草图,再根据图形确定被积函数以及积分的上、下限 . 2. 定积分只能用于求曲边梯形的面积,对于非规则曲边梯形,一般要将其分割或补形为规则曲边梯形,再利用定积分的和与差求面积 . 对于分割或补形中的多边形的面积,可直接利用相关面积公式求解 . 3. 位于 x 轴下方的曲边梯形的面积,等于相应定积分的相反数 . 一般地,设由直线 x = a , x = b ( a < b ) , y = 0 和曲线 y = f ( x ) 所 围成的曲边梯形的面积为 S ,则 . x y a b y = f ( x ) O y = | f ( x )| 作业: P58 练习: ( 1 ),( 2 ) . P60 习题 1.7B 组: 1 , 2 , 3.查看更多