云南省峨山一中2019-2020学年高一上学期9月月考数学试题 含答案

云南省峨山一中2019-2020学年高一上学期9月月考数学试题 含答案

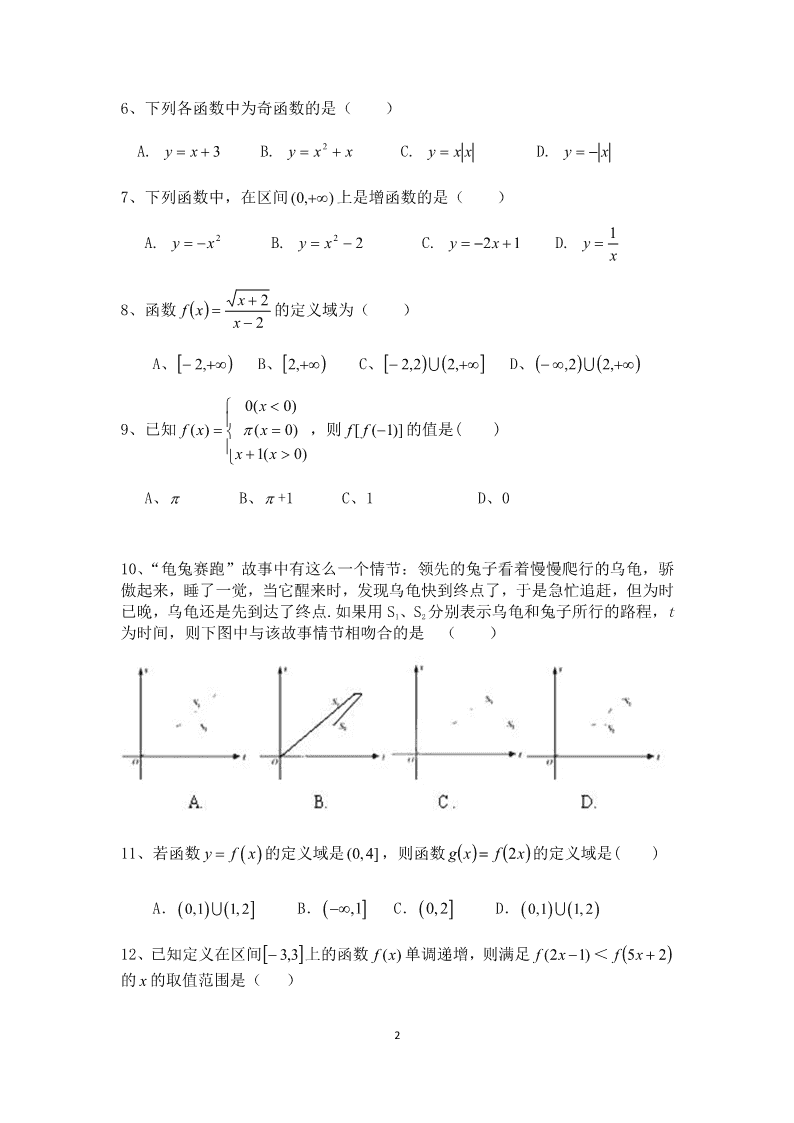
1 云南省峨山一中 2019—2020 学年上学期 9 月考 数学试卷 考生注意：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共 22 个 小题，总分 150 分，考试时间 120 分钟。 第Ⅰ卷（选择题，共 60 分） 一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四个 选项中，只有一个选项符合要求) 1、设集合  1,2,3,4U  ，  1,2,3M  ，N＝{2,3,4},则    NMCU ( ) A．  2,3 B． 2,4 C． 1,4 D． 1,2,3 2、已知集合  0)1(  xxxA ，那么下列结论正确的是（ ） A. A0 B. A1 C. A1 D. A0 3、图中阴影部分表示的集合是( ) A. CU(A∪B) B.（CUA）∩B C.CU(A∩B) D. A∩（CUB） 4、下列函数中，与函数 xy  相同的是 （ ） A. 2)( xy  B. 2xy  C. 3 3xy  D. x xy 2  5、如下图可作为函数 y )(xf 的图像的是( ) A B C D x y O x y O x y O x y O 2 6、下列各函数中为奇函数的是（ ） A. 3 xy B. xxy  2 C. xxy  D. xy  7、下列函数中，在区间 ),0(  上是增函数的是（ ） A. 2xy  B. 22  xy C. 12  xy D. xy 1 8、函数   2 2   x xxf 的定义域为（ ） A、  ,2 B、 ,2 C、    ,22,2  D、    ,22,  9、已知        )0(1 )0( )0(0 )( xx x x xf  ，则 )]1([ ff 的值是( ) A、 B、 +1 C、1 D、0 10、“龟兔赛跑”故事中有这么一个情节：领先的兔子看着慢慢爬行的乌龟，骄 傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时 已晚，乌龟还是先到达了终点.如果用 S1、S2 分别表示乌龟和兔子所行的路程，t 为时间，则下图中与该故事情节相吻合的是 （ ） 11、若函数  y f x 的定义域是(0,4] ，则函数    xfxg 2 的定义域是( ) A．   0,1 1,2 B． ,1 C． 0,2 D．   0,1 1,2 12、已知定义在区间 3,3 上的函数 ( )f x 单调递增，则满足 (2 1)f x  ＜  25 xf 的 x 的取值范围是（ ） 3 A． 1,  B． 11, 5     C． 11, 5     D． 1,1 第Ⅱ卷(非选择题，共 90 分) 二、填空题（共 4 个小题，每题 5 分,共 20 分） 13、 1( ) 4 7f x x   的定义域是 . 14、某校高一某班共有 40 人，摸底测验数学成绩 23 人得优，语文成绩 20 人得 优， 两 门都不得优者有 6 人，则两门都得优者有__________人. 15、已知 )(xf 是奇函数，且当 0x 时， 12)( 2  xxf ，那么 )1(f =__________. 16、已知定义在 R 上的偶函数 ( )f x 在 ,0](- 上为减函数，且 1( ) 02f  ，则不等式   0xf 的解集为 三、解答题(本大题共 6 个小题，共 70 分，解答应写出必要的演算步骤或证明 过程)      17 9 1,2,3 3,4,5,6 , 1 ; (2) ( ). A x x B C A B A B C       、(本小题10分）设 是小于 的正整数 ， ， 求： （） 18 、 ( 本 小 题 12 分 ） 全 集 U=R ， 若 集 合  103|  xxA ， 4  | 2 7B x x   ， （1）求 A B ，  BACU  ; （2）若集合 C={ | }x x a ， CB  ，求实数a的取值范围. 219 ( ) ,6 3,14 ) 2 4 ( ) 3 ( ) 2 xf x x f x x f x f x x     、(本小题12分）已知函数 (1)点（ ）在（ 的图象上吗？ （ ）当 时，求 的值； （ ）当 时，求 的值. 20、（本小题 12 分）已知函数 2( ) 2 9f x x x   分别求下列条件下的值 域， （1）定义域是 }83|{  xx (2）定义域是 }2-3|{  xx 5 21、（本小题 12 分）已知函数 ( )f x 是定义在 R 上的偶函数，且当 x ≤0 时， ( )f x 2 2x x  ． (1)现已画出函数 ( )f x 在 y 轴左侧的图像，如图所示，请补出完整函 数 ( )f x 的图像，并根据图像写出函数 ( )f x 的增区间； (2)求出函数 ( )f x 的解析式和值域. 22、（本小题 12 分）已知函数 2( ) 4 4.f x x x         (1) 0,5 ( 2 , 1 ( ), ( ) g x f x x t t t R f x t     若 ，求 ）的值域； （ ）若 求函数 的最小值 的解析式 6 2019-2020 学年 2022 届高一上学期 10 月月考 数学试卷答案 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C A D C D C B C A B C B 二、填空题 13、 7 4x x      14、9 15、-1 16、 1 1,2 2     三、解答题 17、解：         1,2,3,4,5,6,7,8 1 1,2,3 ......(5 2 3 , ( ) 1,2 3,4,5,6,7,8 ....(10 A A B B C A B C         ，（） 分） （ ） ， 分） 18、（1）  | 3 7A B x x   （3 分）  ( ) | 7 10UC A B x x x   或 ，（6 分） （2） 2a .(12 分） 7 19、  51 (3) 14, 3,4 ( )3 (4) 3. 8 2(3) 2, 14.(126 f f x f x xx          （） 点 不在 的图象上.(4分） (2) （ 分） 由 解得 分） 20、         1 3,8 ( 12,57 . 6 -3,2 ( 8,24 . x f x x f x     （）由二次函数的图象可知：（1）当 时， ） （ 分） （2）当 时， ） （12分） 21、     2 2 2 2 1 -1,0 1 + .(6 2 0, - 0, ( ) 2 , ( ) ( ), ( ) 2 . 2 , 0( ) (12 2 , 0. x x f x x x f x f x f x x x x x xf x x x x                   （）图象略，函数图象关于y轴对称.(3分） 由图象得增区间为： 和 ， 分） （ ）另 则 综上 分） 22、(1)f(x)＝x2－4x－4＝(x－2)2－8， 对称轴 x＝2，开口向上， ∴f(x)在[0，2)上递减，在(2，5]上递增， ∴f(x)的最小值是 f(2)＝－8，f(x)的最大值是 f(5)＝1，故 f(x)的值域为 [－8，1]. (2)f(x)＝x2－4x－4＝(x－2)2－8， 即抛物线开口向上，对称轴为 x＝2，最小值为－8，过点(0，－4)， 结合二次函数的图象可知： 当 t＋1<2，即 t<1 时，f(x)＝x2－4x－4，x∈[t，t＋1](t∈R)，在 x＝t ＋1 处取最小值 f(t＋1)＝t2－2t－7； 8 当 t＋1≥2， t≤2， 即 1≤t≤2 时，f(x)＝x2－4x－4，x∈[t，t＋1](t∈R)在 x ＝2 处取最小值－8； 当 t>2 时，f(x)＝x2－4x－4，x∈[t，t＋1](t∈R)在 x＝t 处取最小值 f(t) ＝t2－4t－4. 综上可得，g(t)＝ t2－2t－7，t∈（－∞，1）， －8，t∈[1，2]， t2－4t－4，t∈（2，＋∞）.