- 2021-06-10 发布 |
- 37.5 KB |
- 8页
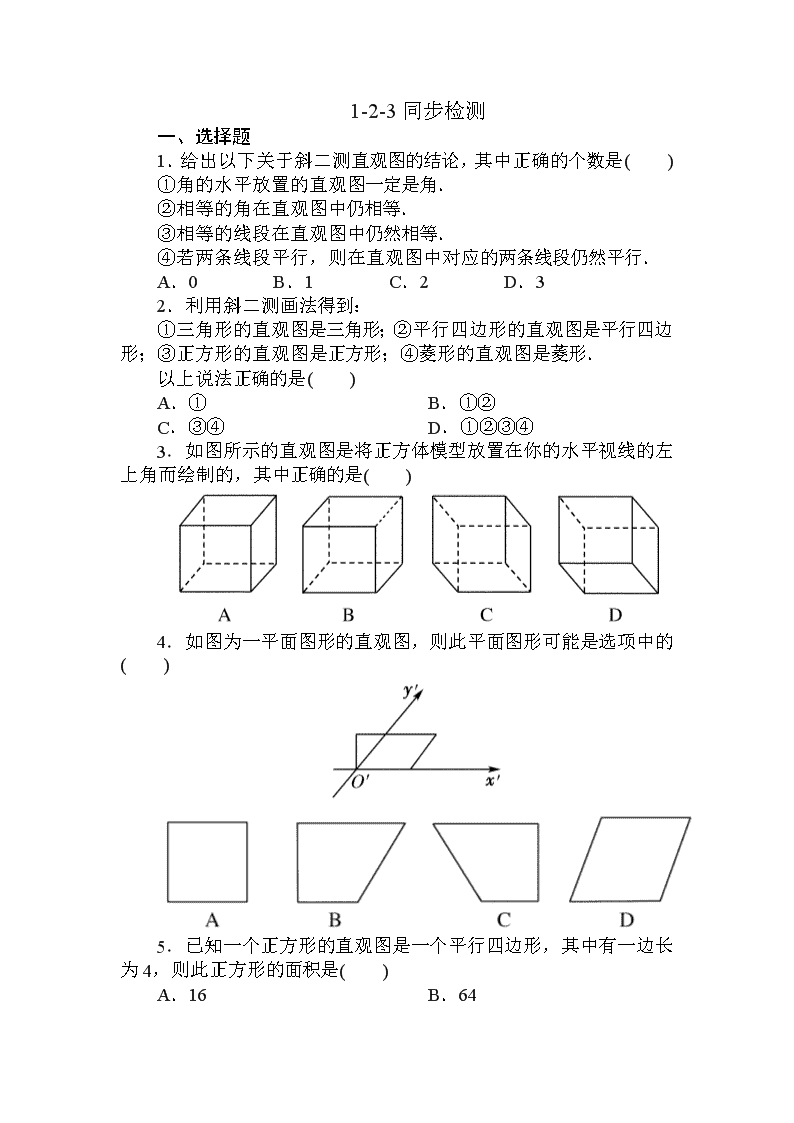
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修2全册同步检测:1-2-3
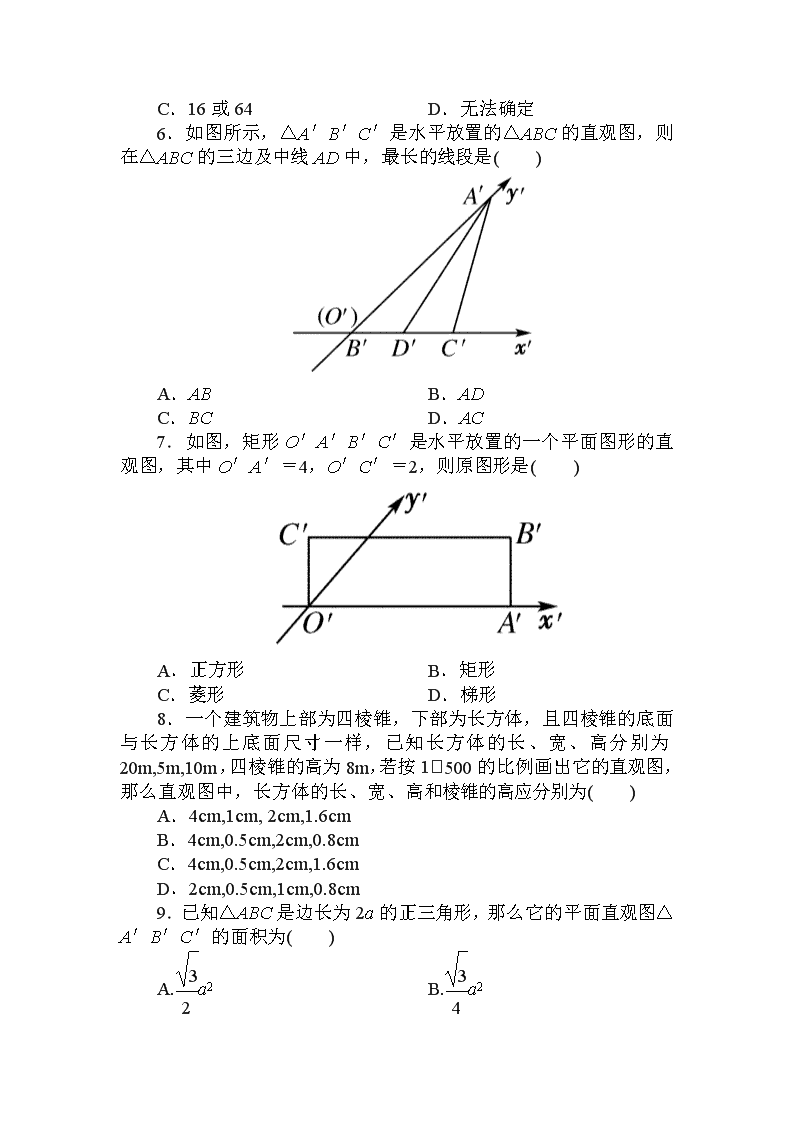
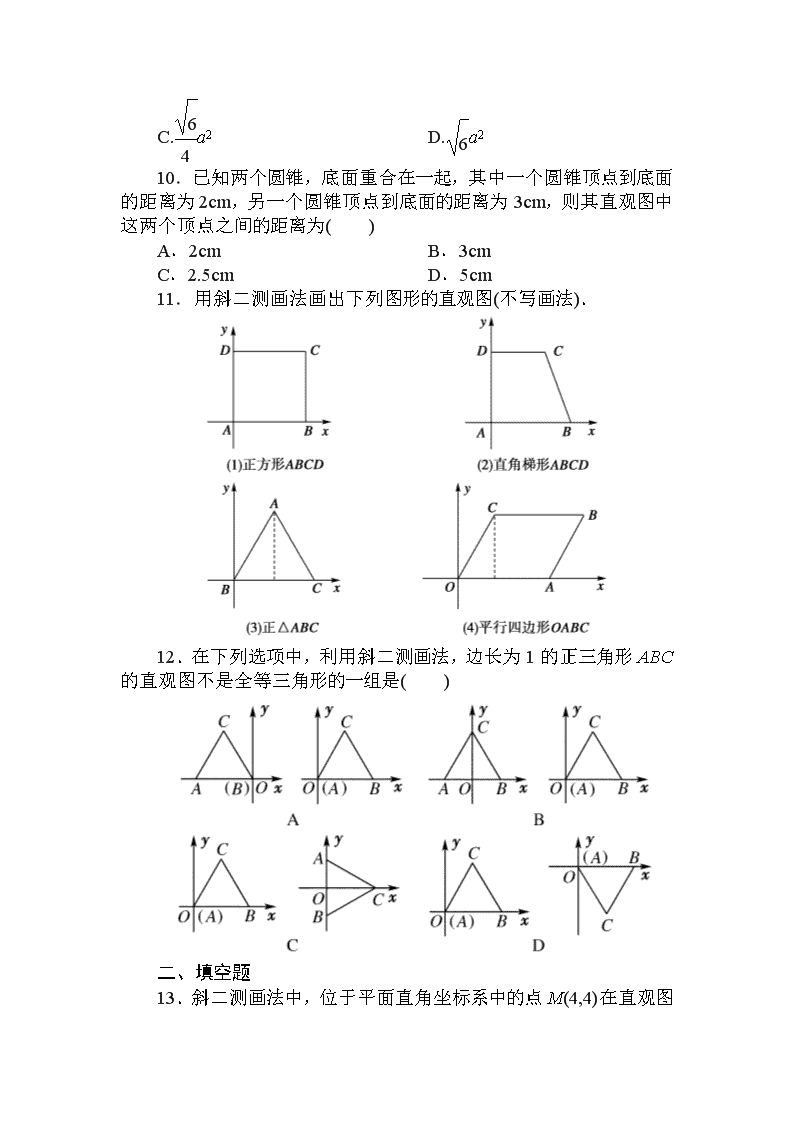
1-2-3同步检测 一、选择题 1.给出以下关于斜二测直观图的结论,其中正确的个数是( ) ①角的水平放置的直观图一定是角. ②相等的角在直观图中仍相等. ③相等的线段在直观图中仍然相等. ④若两条线段平行,则在直观图中对应的两条线段仍然平行. A.0 B.1 C.2 D.3 2.利用斜二测画法得到: ①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形. 以上说法正确的是( ) A.① B.①② C.③④ D.①②③④ 3.如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是( ) 4.如图为一平面图形的直观图,则此平面图形可能是选项中的( ) 5.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积是( ) A.16 B.64 C.16或64 D.无法确定 6.如图所示,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是( ) A.AB B.AD C.BC D.AC 7.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=4,O′C′=2,则原图形是( ) A.正方形 B.矩形 C.菱形 D.梯形 8.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和棱锥的高应分别为( ) A.4cm,1cm, 2cm,1.6cm B.4cm,0.5cm,2cm,0.8cm C.4cm,0.5cm,2cm,1.6cm D.2cm,0.5cm,1cm,0.8cm 9.已知△ABC是边长为2a的正三角形,那么它的平面直观图△A′B′C′的面积为( ) A.a2 B.a2 C.a2 D.a2 10.已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2cm,另一个圆锥顶点到底面的距离为3cm,则其直观图中这两个顶点之间的距离为( ) A.2cm B.3cm C.2.5cm D.5cm 11.用斜二测画法画出下列图形的直观图(不写画法). 12.在下列选项中,利用斜二测画法,边长为1的正三角形ABC的直观图不是全等三角形的一组是( ) 二、填空题 13.斜二测画法中,位于平面直角坐标系中的点M(4,4)在直观图中的对应点是M′,则点M′的坐标为________,点M′ 的找法是________. 14.如下图,水平放置的△ABC的斜二测直观图是图中的△A′B′C′,已知A′C′=6,B′C′=4,则AB边的实际长度是________. 15.如图,是△AOB用斜二测画法画出的直观图,则△AOB的面积是________. 三、解答题 16.如图所示,四边形ABCD是一个梯形,CD∥AB,CD=AO=1,三角形AOD为等腰直角三角形,O为AB的中点,试求梯形ABCD水平放置的直观图的面积. 17.已知几何体的三视图如下,用斜二测画法,画出它的直观图(直接画出图形,尺寸不作要求). 18.如图所示,直角梯形ABCD中,AD∥BC,且AD>BC,该梯形绕边AD所在直线EF旋转一周得一几何体,画出该几何体的直观图和三视图. [分析] 该几何体是一个圆锥和一个圆柱拼接成的简单组合体. 详解答案 1[答案] C [解析] 由斜二测画法规则可知,直观图保持线段的平行性,∴④对,①对;而线段的长度,角的大小在直观图中都会发生改变,∴②③错. 2[答案] B [解析] 根据画法规则,平行性保持不变,与y轴平行的线段长度减半. 3[答案] A [解析] 由几何体直观图画法及立体图形中虚线的使用可知A正确. 4[答案] C [解析] 由直观图一边在x′轴上,一边与y′轴平行,知原图为直角梯形. 5[答案] D 6[答案] D [解析] △ABC是直角三角形,且∠ABC=90°,则AC>AB,AC>AD,AC>BC. 7[答案] C 8[答案] C [解析] 由比例尺可知长方体的长、宽、高和四棱锥的高分别为4cm,1cm,2cm和1.6cm,再结合斜二测画法,可知直观图的相应尺寸应分别为4cm,0.5cm,2cm,1.6cm. 9[答案] C [解析] S△A′B′C′=·2a·a·=a2. 10[答案] D [解析] 圆锥顶点到底面的距离即圆锥的高,故两顶点间距离为2+3=5cm,在直观图中与z轴平行线段长度不变,仍为5cm. 11[解析] 12[答案] C [解析] C中前者画成斜二测直观图时,底AB不变,原来高h变为,后者画成斜二测直观图时,高不变,边AB变为原来的. 13[答案] M′(4,2) 在坐标系x′O′y′中,过点(4,0)和y′ 轴平行的直线与过点(0,2)和x′轴平行的直线的交点即是点M′. [解析] 在x′轴的正方向上取点M1,使O1M1=4,在y′轴上取点M2,使O′M2=2,过M1和M2分别作平行于y′轴和x′轴的直线,则交点就是M′. 14[答案] 10 [解析] 由斜二测画法,可知△ABC是直角三角形,且∠BCA= 90°,AC=6,BC=4×2=8,则AB==10. 15[答案] 16 [解析] 由图易知△AOB中,底边OB=4, 又∵底边OB的高为8, ∴面积S=×4×8=16. 16[解析] 在梯形ABCD中,AB=2,高OD=1,由于梯形ABCD水平放置的直观图仍为梯形,且上底CD和下底AB的长度都不变,如图所示,在直观图中,O′D′=OD,梯形的高D′E′=,于是梯形A′B′C′D′的面积为×(1+2)×=. 17[解] 如图. 18[解析] 直观图如图a所示,三视图如图b所示. 查看更多