2017-2018学年河北省邢台三中高二下学期3月月考数学（文）试题 Word版

2017-2018学年河北省邢台三中高二下学期3月月考数学（文）试题 Word版

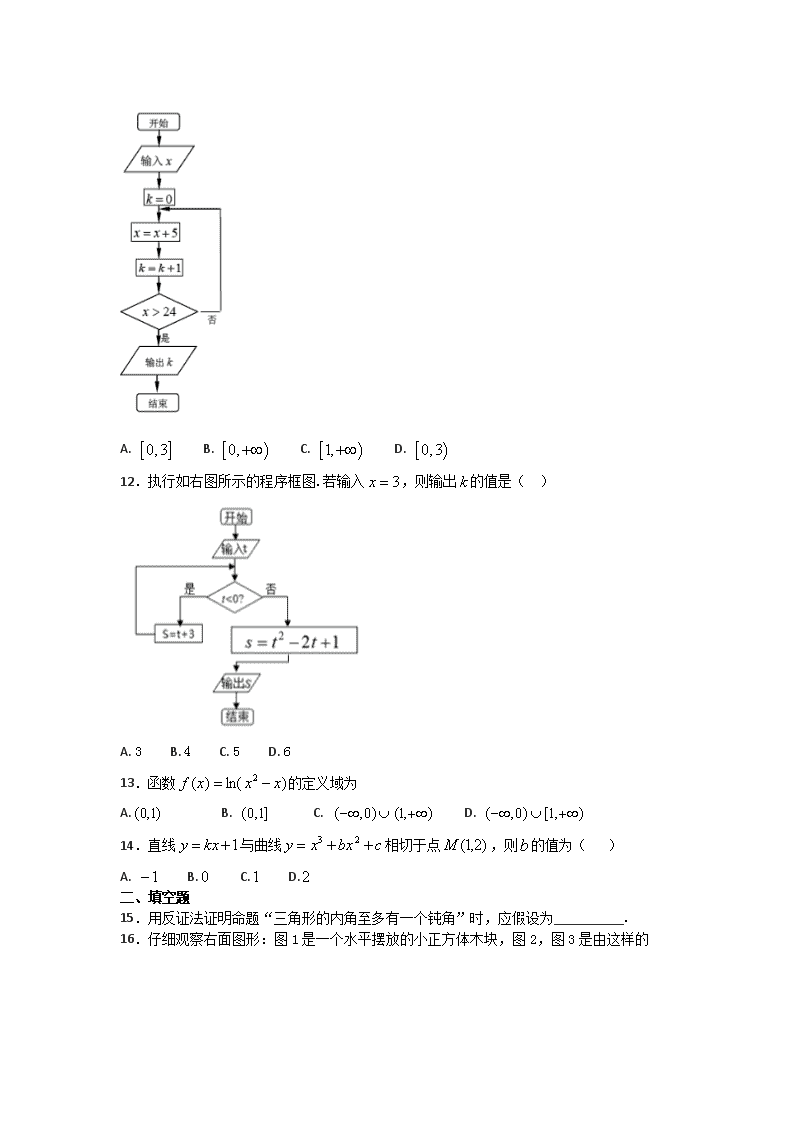
邢台市第三中学 ‎2017-2018学年度第二学期3月月考试题 高二数学试题 分值：150分 时间：90分钟 命题人： 审核人：‎ 注意事项：请将I卷（选择题）答案涂在答题卡上，第II卷（非选择题）答案用黑色钢笔（作图除外）做在答题卡上，不得出框。‎ I卷（选择题 共70分）‎ II卷（非选择题 共80分）‎ 一、单选题 ‎1．复数（i是虚数单位）的虚部为（ ）‎ A. B. ‎1 C. D.‎ ‎2．某家具厂的原材料费支出与销售量（单位：万元）之间有如下数据，根据表中数据，用最小二乘法得出与的线性回归方程为，则为（ ）‎ x ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎25‎ ‎35‎ ‎60‎ ‎55‎ ‎75‎ A. 5 B. ‎15 C. 10 D. 12‎ ‎3．下列数据中，拟合效果最好的回归直线方程，其对应的相关指数为（ ）‎ A. 0.27‎‎ B. ‎0.85 C. 0.96 D. 0.5‎ ‎4．某班主任对全班50名学生进行了作业量多少的调查，数据如下表：‎ 认为作业多 认为作业不多 总数 喜欢玩电脑游戏 ‎18‎ ‎9‎ ‎27‎ 不喜欢玩电脑游戏 ‎8‎ ‎15‎ ‎23‎ 总数 ‎26‎ ‎24‎ ‎50‎ 根据表中数据得到5.059，因为p(K≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）‎ A. 97.5% B. 95% C. 90% D. 无充分根据 ‎5．已知回归方程,则该方程在样本 处的残差为( )‎ A. B. C. D. ‎ ‎6．淮北一中艺术节对摄影类的A，B，C，D四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：‎ 甲说：“是C或D作品获得一等奖”；乙说：“B作品获得一等奖”；‎ 丙说：“A，D两项作品未获得一等奖”；丁说：“是C作品获得一等奖”. ‎ 若这四位同学中只有两位说的话是对的，则获得一等奖的作品是（ ）.‎ A. A作品 B. B作品 C. C作品 D. D作品 ‎7．观察下列各式： ， ， ， ， ，可以得出的一般结论是（ ）‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎8．两旅客坐火车外出旅游，希望座位连在一起，且有一个靠窗，已知火车上的座位如图所示，则下列座位号码符合要求的应当是 A. B. C. D. ‎ ‎9．设复数（为虚数单位），则的共轭复数为（ ）‎ A. B. C. D. ‎ ‎10．已知为虚数单位，若复数满足，则（ ）‎ A. B. C. D. ‎ ‎11．如图所示程序框图，若输入的取值范围为，则输出的取值范围为（ ） ‎ A. B. C. D. ‎ ‎12．执行如右图所示的程序框图.若输入，则输出的值是（ ）‎ A. 3 B. ‎4 C. 5 D. 6‎ ‎13．函数的定义域为 A. B. C. D. ‎ ‎14．直线与曲线相切于点，则的值为（ ）‎ A. B. C. D. ‎ 二、填空题 ‎15．用反证法证明命题“三角形的内角至多有一个钝角”时，应假设为__________．‎ ‎16．仔细观察右面图形：图1是一个水平摆放的小正方体木块，图2，图3是由这样的 小正方体木块叠放而成的，按照这样的规律放下去，至第七个叠放的图形中，小正方体木块总数是_____________‎ ‎17．已知是实数， 是纯虚数，则 ___________.‎ ‎18．已知某几何体的三视图如图，则该几何体的表面积为__________．‎ ‎19．已知z1,z2∈C,|z1+z2|=2,|z1|=2,|z2|=2,则|z1-z2|为________.‎ ‎20．已知复数是纯虚数，（ 为虚数单位)，则__________.‎ 三、解答题 ‎21．某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主). ‎ (1) 根据以上数据完成如下2×2列联表.‎ ‎(2) 能否有99％的把握认为其亲属的饮食习惯与年龄有关?‎ ‎ ‎ ‎22．第31届夏季奥林匹克运动会于‎2016年8月5日至‎8月21日在巴西里约热内卢举行．如表是近五届中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）．‎ 第30届伦敦 第29届北京 第28届雅典 第27届悉尼 第26届亚特兰大 中国 ‎38‎ ‎51‎ ‎32‎ ‎28‎ ‎16‎ 俄罗斯 ‎24‎ ‎23‎ ‎27‎ ‎32‎ ‎26‎ ‎（1）根据表格中两组数据在答题卡上完成近五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；‎ ‎（2）如表是近五届奥运会中国代表团获得的金牌数之和（从第26届算起，不包括之前已获得的金牌数）随时间变化的数据：‎ 时间（届）‎ ‎26‎ ‎27‎ ‎28‎ ‎29‎ ‎30‎ 金牌数之和（枚）‎ ‎16‎ ‎44‎ ‎76‎ ‎127‎ ‎165‎ 作出散点图如图：‎ 由图可以看出，金牌数之和与时间之间存在线性相关关系，请求出关于的线性回归方程，并预测到第32届奥运会时中国代表团获得的金牌数之和为多少？‎ 附：对于一组数据， ，…， ，其回归直线 的斜率和截距的最小二乘估计分别为：‎ ‎，‎ ‎23．一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是该作品前四步时对应的图案，按照此规律，第步完成时对应图案中所包含小正方形的个数记为．‎ ‎（1）求出的值；‎ ‎（2）利用归纳推理，归纳出的关系式；‎ ‎（3）猜想的表达式，并写出推导过程．‎ ‎24．如图，已知四棱锥，其中∥，‎ ‎(1)证明：∥；‎ ‎(2)证明：；‎ ‎(3)求三棱锥的体积.‎ ‎3月月考高二文数参考答案 ‎1．B2．C3．C4．A5．D6．B7．C8．D9．B10．C11．D12．C13．C14．A ‎15．三角形的内角至少有两个钝角 16．91 17． 18． 19．2‎ ‎20． 21．‎ ‎2×2列联表如下所示:‎ 由题意,随机变量的观测值 故有99％的把握认为其亲属的饮食习惯与年龄有关.‎ ‎22．（1）中国代表团获得的金牌数的平均数大于俄罗斯代表团的金牌平均数；俄罗斯代表团获得的金牌数较集中，中国代表团获得的金牌数较分散．（2），金牌数之和238‎ ‎（2）因为， ， ， ，‎ 所以， ，‎ 所以金牌数之和关于时间的线性回归方程为，‎ 当时，中国代表团获得的金牌数之和的预报值，‎ 故预测到第32届奥运会时中国代表团获得的金牌数之和为238枚．‎ ‎23．（1）5，13，25，41（2）（3）‎ ‎【解析】（1）由题图可得，，，观察题图可得.‎ ‎（2）， ，‎ ‎， ，‎ 归纳：.‎ ‎（3）由（2）知，‎ ‎， ，‎ ‎， ，‎ 以上各式相加得，‎ 又， 所以.‎ ‎24．(1)见解析(2)见解析(3) 【解析】试题分析：（1）取的中点连接，构建平行四边形得到，从而证得平面；（2）要证平面平面，转证即可；（3）因为为边上的中点，，利用等积变换有，从而求得三棱锥的体积.‎ 试题解析：‎ ‎（Ⅰ）证明：如图，取的中点连接 因为为边上的中点，所以，且，‎ 因为，， 所以且所以四边形是平行四边形，‎ 所以，又，，‎ 所以平面． ‎ ‎（Ⅱ）证明：在直角梯形中，，‎ 所以 所以，所以，①‎ 又，所以，② 又，所以，‎ 因为， 所以平面 平面． ‎ ‎（III）解：因为为边上的中点，，‎ 所以，‎ 因为，， 所以． ‎