2018届二轮复习第72讲　统计与统计案例课件（全国通用）

2018届二轮复习第72讲　统计与统计案例课件（全国通用）

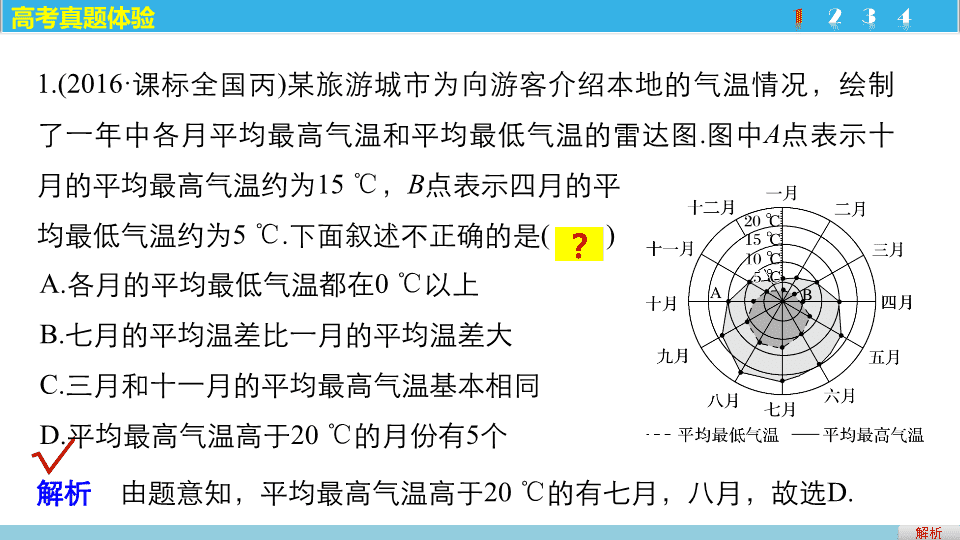
第 2 讲　统计与统计案例 专题七　概率与统计 栏目索引 高考 真题体验 1 热点 分类突破 2 高考 押题精练 3 1.(2016· 课标全国丙 ) 某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图 . 图中 A 点表示十月的平均最高气温约为 15 ℃ ， B 点表示四月 的平 均 最低气温约为 5 ℃ . 下面叙述不正确的是 ( 　　 ) 解析 √ 高考真题 体验 1 2 3 4 A. 各月的平均最低气温都在 0 ℃ 以上 B. 七月的平均温差比一月的平均温差大 C. 三月和十一月的平均最高气温基本相同 D. 平均最高气温高于 20 ℃ 的月份有 5 个 解析　 由题意知，平均最高气温高于 20 ℃ 的有七月，八月，故选 D. A.56 B.60 C.120 D.140 2.(2016· 山东 ) 某高校调查了 200 名学生每周的自习时间 ( 单位：小时 ) ，制成了如图所示的频率分布直方图，其中自习时间的范围是 [17.5,30] ，样本数据分组为 [17.5,20) ， [20,22.5) ， [22.5,25) ， [25,27.5) ， [27.5,30]. 根据直方图，这 200 名学生中每周的自习时间不少于 22.5 小时的人数是 ( 　　 ) 解析 1 2 3 4 √ 解析　 设所求人数为 N ，则 N ＝ 2.5 × (0.16 ＋ 0.08 ＋ 0.04) × 200 ＝ 140 ，故选 D. 1 2 3 4 3.(2016· 北京 ) 某学校运动会的立定跳远和 30 秒跳绳两个单项比赛分成预赛和决赛两个阶段 . 下表为 10 名学生的预赛成绩，其中有三个数据模糊 . 学生序号 1 2 3 4 5 6 7 8 9 10 立定 跳远 ( 单位：米 ) 1.96 1.92 1.82 1.80 1.78 1.76 1.74 1.72 1.68 1.60 30 秒 跳绳 ( 单位：次 ) 63 a 75 60 63 72 70 a － 1 b 65 在这 10 名学生中，进入立定跳远决赛的有 8 人，同时进入立定跳远决赛和 30 秒跳绳决赛的有 6 人，则 ( 　　 ) A.2 号学生进入 30 秒跳绳 决赛 B.5 号学生进入 30 秒跳绳决赛 C.8 号学生进入 30 秒跳绳 决赛 D.9 号学生进入 30 秒跳绳决赛 1 2 3 4 解析 √ 解析　 由数据可知，进入立定跳远决赛的 8 人为： 1 ～ 8 号 ， 所以 进入 30 秒跳绳决赛的 6 人需要从 1 ～ 8 号产生 ， 数据 排序后可知第 3,6,7 号必须进跳绳决赛，另外 3 人需从 63 ， a, 60,63 ， a － 1 五个得分中抽取，若 63 分的人未进决赛 ， 则 60 分的人就会进入决赛，与事实矛盾，所以 63 分必进决赛 . 故选 B. 4.(2016· 上海 ) 某次体检， 6 位同学的身高 ( 单位：米 ) 分别为 1.72,1.78,1.75,1.80,1.69,1.77 ，则这组数据的中位数是 ________( 米 ). 答案 1 2 3 4 1.76 1. 以选择题、填空题的形式考查随机抽样、样本的数字特征、统计图表、回归方程、独立性检验等 ； 2 . 在概率与统计的交汇处命题，以解答题中档难度出现 . 考情考向分 析 返回 热点一　抽样方法 1. 简单随机抽样特点是从总体中逐个抽取 . 适用范围：总体中的个体数较少 . 2. 系统抽样特点是将总体均分成几部分，按事先确定的规则在各部分中抽取 . 适用范围：总体中的个体数较多 . 3. 分层抽样特点是将总体分成几层，分层进行抽取 . 适用范围：总体由差异明显的几部分组成 . 热点分类突破 例 1 　 (1) 某校要从高一、高二、高三共 2 012 名学生中选取 50 名组成志愿团，若采用下面的方法选取，先用简单随机抽样的方法从 2 012 人中剔除 12 人，剩下的 2 000 人再按分层抽样的方法进行，则每人入选的概率 ( 　　 ) A. 都相等且 为 B . 都相等且 为 C. 不会相等 D . 均不相等 解析 √ 解析　 根据分层抽样的定义和方法可得，每个个体被抽到的概率都相等，都等于样本容量除以总体容量 ， 所以 每个个体被抽到的概率都 等于 ， 故选 A. (2) 某工厂生产甲、乙、丙三种型号的产品，产品数量之比为 3 ∶ 5 ∶ 7 ，现用分层抽样的方法抽出容量为 n 的样本，其中甲种产品有 18 件，则样本容量 n ＝ ________. 解析答案 思维升华 90 (1) 随机抽样各种方法中，每个个体被抽到的概率都是相等的 ； ( 2) 系统抽样又称 “ 等距 ” 抽样，被抽到的各个号码间隔相同 ； ( 3) 分层抽样满足：各层抽取的比例都等于样本容量在总体容量中的比例 . 思维 升华 跟踪演练 1 　 (1) 要考察某公司生产的 500 克袋装牛奶中三聚氰胺的含量是否超标，现从 800 袋牛奶中抽取 60 袋进行检验，利用随机数法抽取样本时，先将 800 袋牛奶按 000,001 ， … ， 799 进行编号，如果从随机数表第 7 行第 8 列的数开始向右读，则得到的第 4 个样本个体的编号是 ________.( 下面摘取了随机数表第 7 行至第 9 行 ) 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76( 第 7 行 ) 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79( 第 8 行 ) 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54( 第 9 行 ) 解析答案 解析　 由随机数法可知抽取样本个体的编号为 331,572,455,068 ， … ，故第 4 个样本个体的编号为 068. 068 (2) 利用分层抽样的方法在学生总数为 1 200 人的年级中抽出 20 名同学，其中有女生 8 人，则该年级男生的人数约为 ________. 解析　 由于样本容量为 20 ，其中的男生人数为 12 ，从而该年级男生人数约为 1 200 × ＝ 720. 720 解析答案 热点二　用样本估计总体 2. 频率分布直方图中各小长方形的面积之和为 1 . 3 . 利用频率分布直方图求众数、中位数与平均数 利用频率分布直方图求众数、中位数和平均数时易出错，应注意区分这三者 . 在频率分布直方图中： (1) 最高的小长方形底边中点的横坐标即是众数； (2) 中位数左边和右边的小长方形的面积和是相等的； (3) 平均数是频率分布直方图的 “ 重心 ” ，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和 . 例 2 　 (1) 在某次测量中得到的 A 样本数据如下： 42,43,46,52,42,50 ，若 B 样本数据恰好是 A 样本数据每个都减 5 后所得数据，则 A ， B 两样本的下列数字特征对应相同的是 ( 　　 ) A. 平均数 B . 标准差 C. 众数 D. 中位数 解析 √ 解析　 设样本 A 中的数据为 x i ，则样本 B 中的数据为 y i ＝ x i － 5 ， 则 样本数据 B 中的众数和平均数以及中位数和 A 中的众数，平均数，中位数相差 5 ， 只有 标准差没有发生变化，故选 B. 思维升华 (2) 若五个数 1,2,3,4 ， a 的平均数为 3 ，则这五个数的标准差是 ________. 所以 10 ＋ a ＝ 15 ，即 a ＝ 5 ； 由标准差的计算公式可得 解析答案 (1) 反映样本数据分布的主要方式：频率分布表、频率分布直方图、茎叶图 . 关于频率分布直方图要明确每个小矩形的面积即为对应的频率，其高低能够描述频率的大小，高考中常常考查频率分布直方图的基本知识，同时考查借助频率分布直方图估计总体的概率分布和总体的特征数，具体问题中要能够根据公式求解数据的平均数、众数、中位数和方差等 . ( 2) 由样本数据估计总体时，样本方差越小，数据越稳定，波动越小 . 思维 升华 跟踪演练 2 　 (1) 某学生在一门功课的 22 次考试中，所得分数茎叶图如图所示，则此学生该门功课考试分数的极差与中位数之和为 ( 　　 ) 解析 A.117 B.118 C.118.5 D.119.5 √ 解析　 22 次考试中，所得分数最高的为 98 ，最低的为 56 ， 所以 极差为 98 － 56 ＝ 42 ，将分数从小到大排列，中间两数为 76,76 ， 所以 中位数为 76 ，所以此学生该门功课考试分数的极差与中位数之和为 42 ＋ 76 ＝ 118. (2) 某学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为 n 且支出在 [20,60] 元的样本，其频率分布直方图如图所示，其中支出在 [50,60] 元的学生有 30 人，则 n 的值为 ( 　　 ) 解析 A.100 B.1 000 C.90 D.900 √ 解析　 支出在 [50,60] 元的频率为 1 － 0.1 － 0.24 － 0.36 ＝ 0.3 ， 所以 n ＝ 30÷0.3 ＝ 100 ，故选 A. 热点三　统计案例 1. 线性回归方程 解析 √ x 0 1 2 3 y － 1 1 m 8 得 m ＝ 4 ，故选 A. 思维升华 解析 (2)2016 年 3 月 9 日至 15 日，谷歌人工智能系统 “ 阿尔法 ” 迎战围棋冠军李世石，最终结果 “ 阿尔法 ” 以总比分 4 比 1 战胜李世石 . 许多人认为这场比赛是人类的胜利，也有许多人持反对意见，有网友为此进行了调查，在参加调查的 2 548 名男性中有 1 560 名持反对意见， 2 452 名女性中有 1 200 名持反对意见，在运用这些数据说明 “ 性别 ” 对判断 “ 人机大战是人类的胜利 ” 是否有关系时，应采用的统计方法是 ( 　　 ) A. 茎叶图 B . 分层抽样 C. 独立性检验 D . 回归直线方程 √ 解析　 这是独立性检验，因为这里有两个分类变量，一个是性别分为男女，一个是意见分为支持和反对，这样就构成一个 2 × 2 列联表，用独立性检验来验证 “ 性别 ” 对判断 “ 人机大战是人类的胜利 ” 是否有关系 . 思维升华 思维 升华 跟踪演练 3 　 (1) 随机采访 50 名观众对某电视节目的满意度，得到如下列联表： 单位：人   满意 不满意 合计 男 10 20 30 女 15 5 20 合计 25 25 50 附表和公式如下： P ( K 2 ≥ k ) 0.100 0.050 0.010 0.001 k 2.706 3.841 6.635 10.828 解析 根据以上数据可知 ( 　　 ) A. 有 95% 的把握认为对电视节目的满意度与性别无关 B. 有 99% 的把握认为对电视节目的满意度与性别无关 C. 有 99% 的把握认为对电视节目的满意度与性别有关 D. 有 95% 的把握认为对电视节目的满意度与性别有关 ≈ 8.333>6.635 ，所以有 99% 的把握认为对电视节目的满意度与性别有关，故选 C. √ (2) 春节期间， “ 厉行节约，反对浪费 ” 之风悄然吹开，某市通过随机询问 100 名性别不同的居民是否能做到 “ 光盘 ” 行动，得到如下的列联表：   做不到 “ 光盘 ” 能做到 “ 光盘 ” 男 45 10 女 30 15 附： P ( K 2 ≥ k ) 0.10 0.05 0.025 k 2.706 3.841 5.024 解析 返回 A. 在犯错误的概率不超过 1% 的前提下，认为 “ 该市居民能否做到 ‘ 光盘 ’ 与 性别有关 ” B. 在犯错误的概率不超过 1% 的前提下，认为 “ 该市居民能否做到 ‘ 光盘 ’ 与 性别无关 ” C. 有 90% 以上的把握认为 “ 该市居民能否做到 ‘ 光盘 ’ 与性别有关 ” D. 有 90% 以上的把握认为 “ 该市居民能否做到 ‘ 光盘 ’ 与性别无关 ” √ 返回 所以有 90% 以上的把握认为 “ 该市居民能否做到 ‘ 光盘 ’ 与性别有关 ” ，故选 C. 1 2 3 押题依据　 对茎叶图的考查在高考中较为常见，从中提取数字的特征 ( 如平均数、众数、中位数等 ) 是高考命题的热点题型 . 解析 押题依据 高考押题精练 √ 解析　 甲班 10 名学生的数学成绩的平均数为 1 2 3 乙班 10 名学生的数学成绩的平均数为 所以 m 甲 > m 乙 . 故选 A. 2. 某校为了了解高三学生寒假期间的学习情况，抽查了 100 名学生，统计他们每天的平均学习时间，绘成的频率分布直方图如图所示，则这 100 名学生中学习时间在 6 至 10 小时之间的人数为 ________. 1 2 3 解析 押题依据　 频率分布直方图多以现实生活中的实际问题为背景，对图形的理解应用可以考查考生的基本分析能力，是高考的热点 . 押题依据 58 答案 1 2 3 解析　 由图知， (0.04 ＋ 0.12 ＋ x ＋ 0.14 ＋ 0.05) × 2 ＝ 1 ，解得 x ＝ 0.15 ， 所以 学习时间在 6 至 10 小时之间的频率是 (0.15 ＋ 0.14) × 2 ＝ 0.58 ， 所 求人数为 100 × 0.58 ＝ 58. 1 2 3 3. 某车间为了制定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如下： 零件的个数 x ( 个 ) 2 3 4 5 加工的时间 y ( 小时 ) 2.5 3 4 4.5 (1) 在给定的坐标系中画出表中数据的散点图； 1 2 3 解析答案 押题依据　 线性回归分析在生活中具有很强的应用价值，是高考的一个重要考点 . 押题依据 返回 1 2 3 解　 (1) 散点图如图 . 解析答案 1 2 3 返回 (3) 将 x ＝ 10 代入线性回归方程， 故预测加工 10 个零件约需要 8.05 小时 .