2019届二轮复习专题二基本初等函数、函数与方程课件（38张）（全国通用）

2019届二轮复习专题二基本初等函数、函数与方程课件（38张）（全国通用）

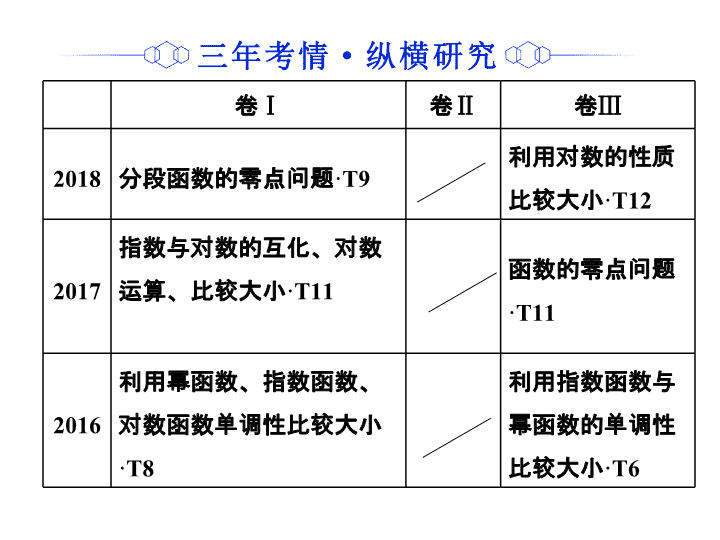
题 二 专 卷 Ⅰ 卷 Ⅱ 卷 Ⅲ 2018 分段函数的零点问题 ·T9 利用对数的性质比较大小 ·T12 2017 指数与对数的互化、对数运算、比较大小 ·T11 函数的零点问题 ·T11 2016 利用幂函数、指数函数、对数函数单调性比较大小 ·T8 利用指数函数与幂函数的单调性比较大小 ·T6 卷 Ⅰ 卷 Ⅱ 卷 Ⅲ 纵向把握趋势 卷 Ⅰ 3 年 3 考，涉及幂函数、指数函数、对数函数的单调性以及分段函数的零点问题，题型为选择题，难度适中，预计 2019 年会以对数的运算、对数函数的图象与性质为考查重点 卷 Ⅱ 3 年 0 考，预计 2019 年会以选择题的形式考查幂函数、指数函数、对数函数的有关性质或大小比较问题 卷 Ⅲ 3 年 3 考，涉及由函数零点个数确定参数问题以及指数、对数、幂函数的性质、比较大小问题．题型为选择题，难度偏大，预计 2019 年仍会考查指数函数、对数函数、幂函数性质的应用 横向把握重点 1. 基本初等函数作为高考的命题热点，多考查指数式与对数式的运算，利用函数的性质比较大小，一般出现在第 5 ～ 12 题的位置，有时难度较大． 2. 函数的应用问题多体现在函数零点与方程根的综合问题上，题目可能较难，应引起重视 . 考法一 基本初等函数的图象与性质 [ 答案 ] D [ 答案 ] B [ 答案 ] D 先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解 数形 结合法 先将参数分离，转化为求函数值域的问题加以解决 分离 参数法 直接根据题设条件构建关于参数的不等式 ( 组 ) ，再通过解不等式 ( 组 ) 确定参数的取值范围 直接法 答案： D 答案： D “专题跟踪检测”见 专题跟踪检测（二） ( 单击进入电子文档 ) 谢谢观看