四川省宜宾市叙州区第二中学校2019-2020学年高二下学期第四学月考试数学（理）试题

四川省宜宾市叙州区第二中学校2019-2020学年高二下学期第四学月考试数学（理）试题

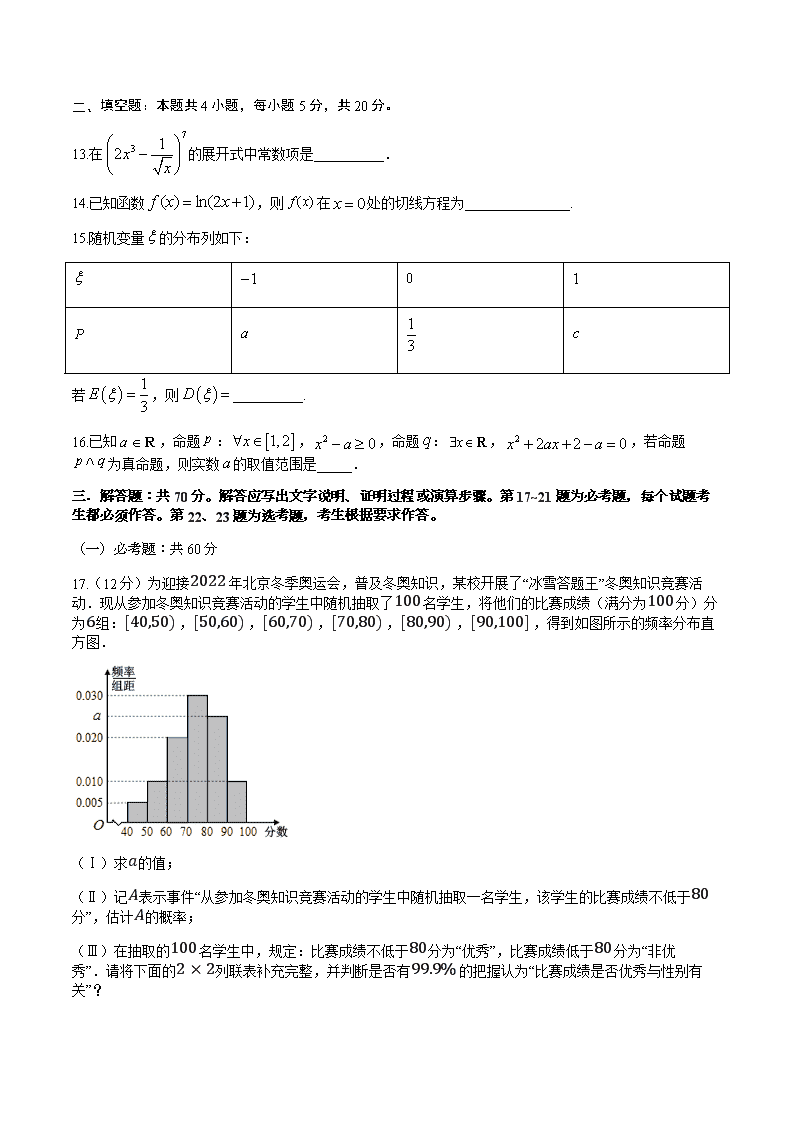
‎2020年春四川省宜宾市叙州区第二中学高二第四学月考试 理科数学 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。‎ 第I卷 选择题（60分）‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知集合，则 ‎ A. B. C. D. ‎ ‎2.已知复数,则的共轭复数 ‎ A. B. C. D.‎ ‎3.《高中数学课程标准》(2017 版)规定了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平，现以六大素养为指标对二人进行了测验，根据测验结果绘制了雷达图(如图，每项指标值满分为‎5‎分，分值高者为优)，则下面叙述正确的是 ‎ ‎(注:雷达图(Radar Chart)，又可称为戴布拉图、蜘蛛网图(Spider Chart)，可用于对研究对象的多维分析)‎ A.甲的数据分析素养高于乙 B.甲的数学建模素养优于数学抽象素养 C.乙的六大素养中逻辑推理最差 D.乙的六大素养整体水平优于甲 ‎4.若，则“”是 “”的 ‎ A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 ‎5.函数y=‎2‎‎|x|‎sin2x的图象可能是 A. B. C. D. ‎ ‎6.已知随机变量服从正态分布,,则 A. B. C. D. ‎ ‎7.5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方法共有 A. 10种 B. 20种 C. 25种 D. 32种 ‎8.甲、乙、丙三人每人准备在‎3‎个旅游景点中各选一处去游玩，则在“至少有‎1‎个景点未被选择”的条件下，恰有‎2‎个景点未被选择的概率是 ‎ A. B. C. D.‎ ‎9.若函数fx=kx−lnx在区间‎1,+∞‎单调递增，则k的取值范围是 ‎ A. ‎−∞,−2‎ B. ‎−∞,−1‎ C. ‎2,+∞‎ D. ‎‎1,+∞‎ ‎10.已知函数，x∈R，若a=flog‎1‎‎2‎‎3‎，b=flog‎1‎‎3‎‎2‎，c=f‎2‎‎−2‎则a,b,c的大小为 ‎ A.a>b>c B.b>c>a C.c>b>a D.‎b>a>c ‎11.已知是定义在上的函数，若且，则的解集为 ‎ A. B. C. D. ‎ ‎12.已知函数，且对任意的，都有恒成立，则的最大值为 ‎ A. B. C. D. ‎ 第II卷 非选择题（90分）‎ 二、 填空题：本题共4小题，每小题5分，共20分。‎ ‎13.在的展开式中常数项是__________．‎ ‎14.已知函数，则在处的切线方程为_______________.‎ ‎15.随机变量的分布列如下：‎ 若，则__________.‎ ‎16.已知，命题：，，命题：，，若命题为真命题，则实数的取值范围是_____．‎ 三．解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：共60分 ‎17.（12分）为迎接‎2022‎年北京冬季奥运会，普及冬奥知识，某校开展了“冰雪答题王”冬奥知识竞赛活动．现从参加冬奥知识竞赛活动的学生中随机抽取了‎100‎名学生，将他们的比赛成绩（满分为‎100‎分）分为‎6‎组：‎[40,50)‎，‎[50,60)‎，‎[60,70)‎，‎[70,80)‎，‎[80,90)‎，‎[90,100]‎，得到如图所示的频率分布直方图．‎ ‎（Ⅰ）求a的值；‎ ‎（Ⅱ）记A表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生，该学生的比赛成绩不低于‎80‎分”，估计A的概率；‎ ‎（Ⅲ）在抽取的‎100‎名学生中，规定：比赛成绩不低于‎80‎分为“优秀”，比赛成绩低于‎80‎分为“非优秀”．请将下面的‎2×2‎列联表补充完整，并判断是否有‎99.9%‎的把握认为“比赛成绩是否优秀与性别有关”？‎ 优秀 非优秀 合计 男生 ‎40‎ 女生 ‎50‎ 合计 ‎100‎ 参考公式及数据：K‎2‎‎=‎n‎(ad−bc)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎，n=a+b+c+d．‎ P(K‎2‎≥k‎0‎)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k‎0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎18（12分）.已知函数.‎ ‎(I)讨论函数的单调性;‎ ‎(II)对于任意正实数x,不等式恒成立,求实数k的取值范围.‎ ‎19.（12分）如图，已知三棱柱，平面平面,，分别是的中点.‎ ‎(I)证明：；‎ ‎（2）求直线与平面所成角的余弦值.‎ ‎20.（12分）已知椭圆C：x‎2‎a‎2‎‎+y‎2‎b‎2‎=1(a>b>0)‎的一个焦点为F(1,0)‎，点P‎2‎‎3‎‎,‎‎2‎‎6‎‎3‎在C上.‎ ‎(I)求椭圆C的方程；‎ ‎（2）若直线l：y=x+m与椭圆C相交于A，B两点，问y轴上是否存在点M，使得ΔABM是以M为直角顶点的等腰直角三角形？若存在，求点M的坐标；若不存在，说明理由.‎ ‎21.（12分）已知函数f(x)=xlnx，g(x)=‎1‎‎2‎mx‎2‎+x.‎ ‎(I)若函数f(x)‎与g(x)‎的图像上存在关于原点对称的点，求实数m的取值范围；‎ ‎（II）设F(x)=f(x)−g(x)‎，已知F(x)‎在‎(0,+∞)‎上存在两个极值点x‎1‎‎,‎x‎2‎，且x‎1‎‎<‎x‎2‎，求证：x‎1‎x‎2‎‎>‎e‎2‎（其中e为自然对数的底数）.‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22．[选修4-4：坐标系与参数方程]（10分）‎ 如图，在极坐标系中，，，，，，弧，所在圆的圆心分别是，，曲线是弧，曲线是线段，曲线是线段，曲线是弧.‎ ‎(I)分别写出，，，的极坐标方程；‎ ‎（II）曲线由，，，构成，若点，（），在 上，则当时，求点的极坐标.‎ ‎23．[选修4-5：不等式选讲]（10分）‎ 设 ‎(I)解不等式；‎ ‎（II）对任意的非零实数，有恒成立，求实数的取值范围.‎ ‎2020年春四川省宜宾市叙州区第二中学高二第四学月考试 理科数学答案 ‎1.C 2.A 3.D 4.A 5.D 6.D 7.D 8.A 9.D 10.C 11.D 12.B ‎13.14 14. 15. 16.或 ‎17.（Ⅰ）由题可得‎(0.005+0.010+0.020+0.030+a+0.010)×10=1‎，‎ 解得a=0.025‎．‎ ‎（Ⅱ）由（Ⅰ）知a=0.025‎，‎ 则比赛成绩不低于‎80‎分的频率为‎(0.025+0.010)×10=0.35‎，‎ 故从参加冬奥知识竞赛活动的学生中随机抽取一名学生，该学生的比赛成绩不低于‎80‎分的概率约为‎0.35‎．‎ ‎（Ⅲ）由（Ⅱ）知，在抽取的‎100‎名学生中，比赛成绩优秀的有‎100×0.35=35‎人，‎ 由此可得完整的‎2×2‎列联表：‎ 优秀 非优秀 合计 男生 ‎10‎ ‎40‎ ‎50‎ 女生 ‎25‎ ‎25‎ ‎50‎ 合计 ‎35‎ ‎65‎ ‎100‎ 所以K‎2‎的观测值k=‎100×‎‎(10×25-25×40)‎‎2‎‎35×65×50×50‎=‎900‎‎91‎≈9.890<10.828‎，‎ 所以没有‎99.9%‎的把握认为“比赛成绩是否优秀与性别有关”．‎ ‎18.(1)因为.所以,令,得,‎ 当时,;当时,‎ 所以函数在上单调递减,在上单调递增.‎ ‎(2)由于,恒成立,所以.‎ 构造函数,所以.‎ 令,解得,当时,,当时,.‎ 所以函数在点处取得最小值,即.‎ 因此所求k的取值范围是.‎ ‎19.(1)如图所示，连结，‎ 等边中，，则，‎ 平面ABC⊥平面，且平面ABC∩平面，‎ 由面面垂直的性质定理可得：平面，故，‎ 由三棱柱的性质可知，而，故，且，‎ 由线面垂直的判定定理可得：平面，‎ 结合⊆平面，故.‎ ‎(2)在底面ABC内作EH⊥AC，以点E为坐标原点，EH,EC,方向分别为x,y,z轴正方向建立空间直角坐标系.‎ 设，则，,，‎ 据此可得：，‎ 由可得点的坐标为，‎ 利用中点坐标公式可得：，由于，‎ 故直线EF的方向向量为：‎ 设平面的法向量为，则：‎ ‎，‎ 据此可得平面的一个法向量为，‎ 此时，‎ 设直线EF与平面所成角为，则.‎ ‎20.‎(1)‎由题意可得c=1‎，点P(‎2‎‎3‎,‎2‎‎6‎‎3‎)‎在C上，‎∴‎4‎‎9‎a‎2‎+‎8‎‎3‎b‎2‎=1‎，‎ 又a‎2‎‎=b‎2‎+c‎2‎=b‎2‎+1‎，解得a‎2‎‎=4‎，b‎2‎‎=3‎，‎∴‎椭圆C的方程为x‎2‎‎4‎‎+y‎2‎‎3‎=1‎，‎ ‎(2)‎假设y轴上存在点M(0,t)‎，‎△ABM是以M为直角顶点的等腰直角三角形，‎ 设A(x‎1‎,y‎1‎)‎，B(x‎2‎,y‎2‎)‎，线段AB的中点为N(x‎0‎,y‎0‎)‎，‎ 由x‎2‎‎4‎‎+y‎2‎‎3‎=1‎y=x+m，消去y可得‎7x‎2‎+8mx+4m‎2‎-12=0‎，‎ ‎△=64m‎2‎-28(4m‎2‎-12)=16(21-3m‎2‎)>0‎‎，解得m‎2‎‎<7‎，‎ ‎∴x‎1‎+x‎2‎=-‎‎8m‎7‎‎，x‎1‎x‎2‎‎=‎‎4m‎2‎-12‎‎7‎，‎ ‎∴x‎0‎=-x‎1‎‎+‎x‎2‎‎2‎=-‎‎4m‎7‎‎，y‎0‎‎=x‎0‎+m=‎‎3m‎7‎，‎ ‎∴N(-‎4m‎7‎,‎3m‎7‎)‎‎，依题意有AM⊥BM，MN⊥l，‎ 由MN⊥l，可得t-‎‎3m‎7‎‎0-(-‎4m‎7‎)‎‎×1=-1‎，可得t=-‎m‎7‎，‎ 由AM⊥BM可得y‎1‎‎-tx‎1‎‎⋅y‎2‎‎-tx‎2‎=-1‎，‎∵y‎1‎=x‎1‎+m，y‎2‎‎=x‎2‎+m，‎ 代入上式化简可得‎2x‎1‎x‎2‎+2(m-t)(x‎1‎+x‎2‎)+(m-t‎)‎‎2‎=0‎，‎ 则‎2(4m‎2‎-12)‎‎7‎‎-(‎8m‎7‎‎)‎‎2‎+(‎8m‎7‎‎)‎‎2‎=0‎，解得m=±‎‎3‎，‎ 当m=‎‎3‎时，点M(0,-‎3‎‎7‎)‎满足题意，当m=-‎‎3‎时，点M(0,‎3‎‎7‎)‎满足题意 ‎21.（1）函数fx与gx的图像上存在关于原点对称的点 即gx=‎1‎‎2‎mx‎2‎+x的图像与函数y=−f‎−x=xln‎−x的图像有交点 即‎1‎‎2‎mx‎2‎+x=xln‎−x在‎−∞,0‎有解，即‎1‎‎2‎m=‎ln‎−x−1‎x在‎−∞,0‎上有解 设φx=‎ln‎−x−1‎x，x<0‎，则φ‎′‎x‎=‎‎2−ln‎−xx‎2‎ 当x∈‎‎−∞,−‎e‎2‎时，φx为减函数；当x∈‎‎−e‎2‎,0‎时，φx为增函数 φxmin=φ‎−‎e‎2‎=−‎‎1‎e‎2‎‎，即m≥−‎‎2‎e‎2‎ ‎（2）Fx=fx−gx=xlnx−‎1‎‎2‎mx‎2‎−x，‎F‎′‎x‎=lnx−mx Fx在‎0,+∞‎上存在两个极值点x‎1‎‎,‎x‎2‎，且x‎1‎‎<‎x‎2‎ ‎‎∴‎lnx‎1‎−mx‎1‎=0‎lnx‎2‎−mx‎2‎=0‎ ‎∴m=‎lnx‎1‎+lnx‎2‎x‎1‎‎+‎x‎2‎且m=‎lnx‎1‎−lnx‎2‎x‎1‎‎−‎x‎2‎ ‎∴lnx‎1‎+lnx‎2‎x‎1‎‎+‎x‎2‎=‎lnx‎1‎−lnx‎2‎x‎1‎‎−‎x‎2‎‎，即lnx‎1‎+lnx‎2‎=x‎1‎‎+‎x‎2‎x‎1‎‎−‎x‎2‎lnx‎1‎x‎2‎=‎x‎1‎x‎2‎‎+1‎lnx‎1‎x‎2‎x‎1‎x‎2‎‎−1‎ 设t=x‎1‎x‎2‎∈‎‎0,1‎，则lnx‎1‎+lnx‎2‎=‎t+1‎lntt−1‎ 要证x‎1‎x‎2‎‎>‎e‎2‎，即证lnx‎1‎+lnx‎2‎>2‎ 只需证明t+1‎lntt−1‎‎>2‎，即证明lnt−‎2‎t−1‎t+1‎<0‎ 设ht=lnt−‎‎2‎t−1‎t+1‎，则h‎′‎t‎=‎1‎t−‎4‎t+1‎‎2‎=t−1‎‎2‎tt+1‎‎2‎>0‎ 则ht=lnt−‎‎2‎t−1‎t+1‎在‎0,1‎上单调递增，‎ht2‎‎ ‎‎∴x‎1‎x‎2‎>‎e‎2‎ ‎22.（1）解法一：在极坐标系下，在曲线上任取一点，连接、，‎ 则在直角三角形中，，，，得：.‎ 所以曲线的极坐标方程为：‎ 又在曲线上任取一点，则在中，，，，‎ ‎，，由正弦定理得：， ‎ 即：，化简得的极坐标方程为：‎ 同理可得曲线，的极坐标方程分别为：，‎ 解法二：（先写出直角坐标方程，再化成极坐标方程.）‎ 由题意可知，，，的直角坐标方程为：‎ ‎，，‎ ‎，，‎ 所以，，，的极坐标方程为：，‎ ‎，，‎ ‎（2）当时，，，‎ 当时，，，‎ 所以点的极坐标为，‎ ‎23.（1）‎ 令 当时 当时 当时 综上所述 ‎（2）恒成立等价于 ‎（当且仅当时取等）‎ 恒成立