数学卷·2018届江苏省盐城市南洋中学高二上学期期中考试数学试卷 (解析版)

数学卷·2018届江苏省盐城市南洋中学高二上学期期中考试数学试卷 (解析版)

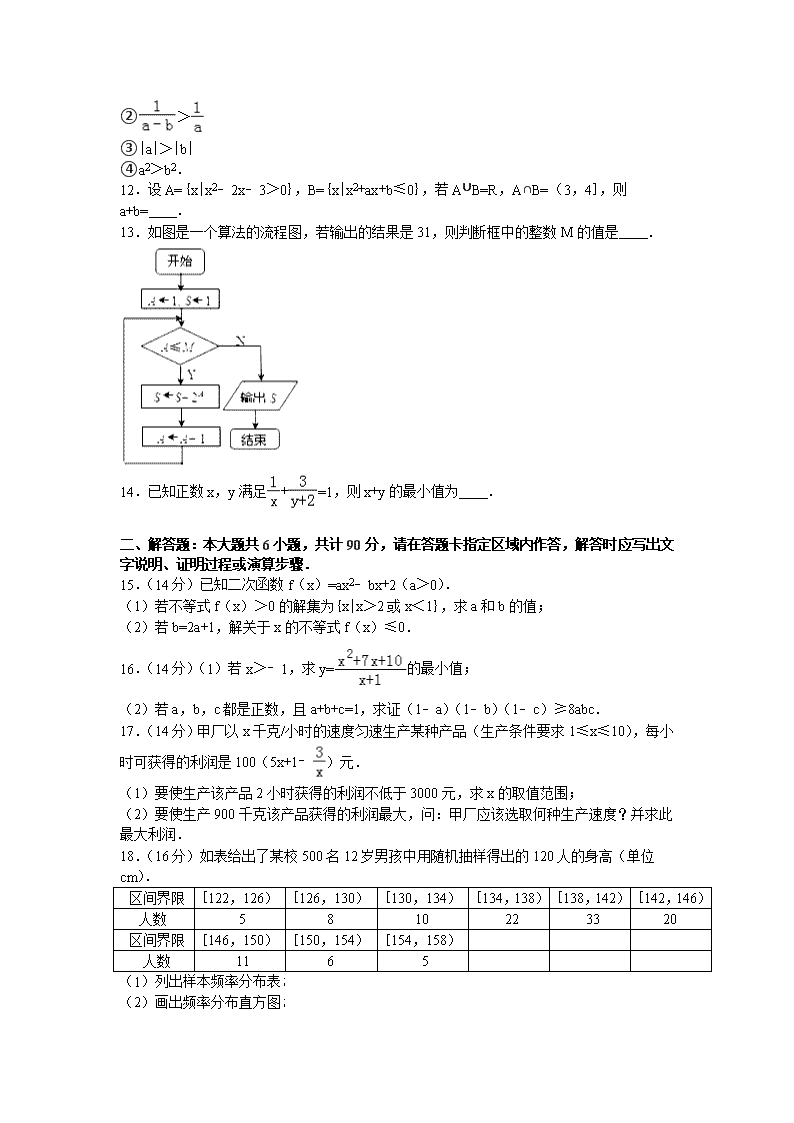
‎2016-2017学年江苏省盐城市南洋中学高二（上）期中数学试卷 ‎　‎ 一、填空题：本大题共14题，每题5分，共计70分，请把答案填写在答题卡相应位置上．‎ ‎1．函数的定义域是　　．‎ ‎2．不等式组，表示的平面区域的面积为　　．‎ ‎3．已知集合M={x|x2﹣3x﹣28≤0}，N={x|x2﹣x﹣2＞0}，则M∩N=　　．‎ ‎4．如果log3m+log3n=4，那么m+n的最小值是　　．‎ ‎5．某校有老师200人，男学生1200人，女学生1000人．现用分层抽样的方法从所有师生中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人，则n=　　．‎ ‎6．已知数据x1，x2，…，x10的方差为3，那么数据2x1+3，2x2+3，…2x10+3的方差为　　．‎ ‎7．将容量为100的样本数据，按从小到大的顺序分成8个组，如表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 频数 ‎9‎ ‎14‎ ‎14‎ ‎13‎ ‎12‎ x ‎13‎ ‎10‎ 则第六组的频率为　　．‎ ‎8．已知变量x，y满足约束条件，则目标函数z=﹣2x+y的取值范围是　　．‎ ‎9．已知x＞，则函数y=4x+的最小值为　　．‎ ‎10．根据如图所示的伪代码，可知输出的结果T为　　．‎ ‎11．若a＜b＜0，则下列不等式中不成立的是　　（只填序号）‎ ‎①＞‎ ‎②＞‎ ‎③|a|＞|b|‎ ‎④a2＞b2．‎ ‎12．设A={x|x2﹣2x﹣3＞0}，B={x|x2+ax+b≤0}，若A∪B=R，A∩B=（3，4]，则a+b=　　．‎ ‎13．如图是一个算法的流程图，若输出的结果是31，则判断框中的整数M的值是　　．‎ ‎14．已知正数x，y满足+=1，则x+y的最小值为　　．‎ ‎　‎ 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15．（14分）已知二次函数f（x）=ax2﹣bx+2（a＞0）．‎ ‎（1）若不等式f（x）＞0的解集为{x|x＞2或x＜1}，求a和b的值；‎ ‎（2）若b=2a+1，解关于x的不等式f（x）≤0．‎ ‎16．（14分）（1）若x＞﹣1，求y=的最小值；‎ ‎（2）若a，b，c都是正数，且a+b+c=1，求证（1﹣a）（1﹣b）（1﹣c）≥8abc．‎ ‎17．（14分）甲厂以x千克/小时的速度匀速生产某种产品（生产条件要求1≤x≤10），每小时可获得的利润是100（5x+1﹣）元．‎ ‎（1）要使生产该产品2小时获得的利润不低于3000元，求x的取值范围；‎ ‎（2）要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求此最大利润．‎ ‎18．（16分）如表给出了某校500名12岁男孩中用随机抽样得出的120人的身高（单位cm）．‎ ‎ 区间界限 ‎[122，126）‎ ‎[126，130）‎ ‎[130，134）‎ ‎[134，138）‎ ‎[138，142）‎ ‎[142，146）‎ 人数 ‎ ‎ 5‎ ‎8 ‎ ‎10 ‎ ‎ 22‎ ‎ 33‎ ‎20 ‎ ‎ 区间界限 ‎[146，150）‎ ‎[150，154）‎ ‎[154，158）‎ ‎ 人数 ‎ 11‎ ‎6 ‎ ‎ 5‎ ‎（1）列出样本频率分布表﹔‎ ‎（2）画出频率分布直方图﹔‎ ‎（3）估计身高小于134cm的人数占总人数的百分比．‎ ‎19．（16分）设函数f（x）=mx2﹣mx﹣1（m≠0），若对于x∈[1，3]，f（x）＜﹣m+5恒成立，求m的取值范围．‎ ‎20．（16分）已知集合A={x|x2﹣2x﹣3≤0}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}．‎ ‎（1）当m=2时，求A∪B；‎ ‎（2）若A∩B=[1，3]，求实数m的值；‎ ‎（3）若A⊆∁RB，求实数m的取值范围．‎ ‎　‎ ‎2016-2017学年江苏省盐城市南洋中学高二（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、填空题：本大题共14题，每题5分，共计70分，请把答案填写在答题卡相应位置上．‎ ‎1．（2016秋•亭湖区校级期中）函数的定义域是　{x|x≥6或x≤﹣3}　．‎ ‎【考点】函数的定义域及其求法．‎ ‎【专题】函数的性质及应用．‎ ‎【分析】根据函数成立的条件即可求函数的定义域．‎ ‎【解答】解：要使函数有意义，则18+3x﹣x2≥0，‎ 即x2﹣3x﹣18≤0，‎ 解得x≥6或x≤﹣3，‎ 故函数的定义域为{x|x≥6或x≤﹣3}，‎ 故答案为：{x|x≥6或x≤﹣3}‎ ‎【点评】本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件 ‎　‎ ‎2．（2016秋•亭湖区校级期中）不等式组，表示的平面区域的面积为　　．‎ ‎【考点】简单线性规划．‎ ‎【专题】计算题；数形结合；方程思想；转化思想；不等式．‎ ‎【分析】先画出约束条件的可行域，并由图形选择合适的公式求解面积．‎ ‎【解答】解：满足约束条件的可行域如下图示：A（，），B（3，﹣3），C（3，8）．‎ 由图可得，图中阴影部分面积为：‎ S=×11×=，‎ 故答案为：．‎ ‎【点评】平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．‎ ‎　‎ ‎3．（2016秋•亭湖区校级期中）已知集合M={x|x2﹣3x﹣28≤0}，N={x|x2﹣x﹣2＞0}，则M∩N=　{x|﹣4≤x＜﹣1或2＜x≤7}，　．‎ ‎【考点】交集及其运算．‎ ‎【专题】计算题；集合思想；定义法；集合．‎ ‎【分析】解一元二次不等式，即可求出已知中集合M={x|x2﹣3x﹣28≤0}，N={x|x2﹣x﹣2＞0}，根据集合交集运算法则，即可得到答案．‎ ‎【解答】解：∵M={x|x2﹣3x﹣28≤0}={x|﹣4≤x≤7}，‎ N={x|x2﹣x﹣2＞0}={x|x＜﹣1，或x＞2}，‎ ‎∴M∩N={x|﹣4≤x≤7}∩{x|x＜﹣1，或x＞2}={x|﹣4≤x＜﹣1或2＜x≤7}，‎ 故答案为：{x|﹣4≤x＜﹣1或2＜x≤7}，‎ ‎【点评】本题考查的知识点是交集及其运算，其中解一元二次不等式，求出两个集合是解答本题的关键．‎ ‎　‎ ‎4．（2008春•江宁区期末）如果log3m+log3n=4，那么m+n的最小值是　18　．‎ ‎【考点】基本不等式；对数的运算性质．‎ ‎【专题】不等式的解法及应用．‎ ‎【分析】利用对数的运算性质和基本不等式即可得出．‎ ‎【解答】解：∵log3m+log3n=4，∴，得mn=34．‎ ‎∵m＞0，n＞0，∴ ==18，当且仅当m=n=9时取等号．‎ 故答案为18．‎ ‎【点评】熟练掌握对数的运算性质和基本不等式是解题的关键．‎ ‎　‎ ‎5．（2004•湖北）某校有老师200人，男学生1200人，女学生1000人．现用分层抽样的方法从所有师生中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人，则n=　192　．‎ ‎【考点】分层抽样方法．‎ ‎【专题】计算题；压轴题．‎ ‎【分析】根据某校有老师200人，男学生1 200人，女学生1 000人，做出全校的人数，根据从女学生中抽取的人数为80人，得到每个个体被抽到的概率，用全校人数乘以概率，得到结果．‎ ‎【解答】解：∵某校有老师200人，男学生1 200人，女学生1 000人．‎ ‎∴学校共有200+1200+1000人 由题意知=，‎ ‎∴n=192．‎ 故答案为：192‎ ‎【点评】本题考查分层抽样的相关知识，容易出错的是不理解分层抽样的含义或与其它混淆．抽样方法是数学中的一个小知识点，但一般不难，故也是一个重要的得分点，不容错过．‎ ‎　‎ ‎6．（2016秋•亭湖区校级期中）已知数据x1，x2，…，x10的方差为3，那么数据2x1+3，2x2+3，…2x10+3的方差为　12　．‎ ‎【考点】极差、方差与标准差．‎ ‎【专题】计算题；方程思想；定义法；概率与统计．‎ ‎【分析】利用方差的性质直接求解．‎ ‎【解答】解：∵x1，x2，…，x10的方差为3，‎ ‎∴数据2x1+3，2x2+3，…2x10+3的方差为：22×3=12．‎ 故答案为：12．‎ ‎【点评】本题考查方差的求法，是基础题，解题时要认真审题，注意方差性质的合理运用．‎ ‎　‎ ‎7．（2016秋•亭湖区校级期中）将容量为100的样本数据，按从小到大的顺序分成8个组，如表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 频数 ‎9‎ ‎14‎ ‎14‎ ‎13‎ ‎12‎ x ‎13‎ ‎10‎ 则第六组的频率为　0.15　．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【专题】计算题；综合法；概率与统计．‎ ‎【分析】由表中数据，根据样本容量为100，我们可计算出第6组频数，代入频率公式：频率=，可得答案 ‎【解答】解：∵第6组频数为100﹣（9+14+14+13+12+13+10）=15‎ ‎∴第6组频率为=0.15‎ 故答案为：0.15‎ ‎【点评】本题考查的知识点是频率分布表，其中熟练掌握频率公式：频率=，是解答的关键 ‎　‎ ‎8．（2012•南京二模）已知变量x，y满足约束条件，则目标函数z=﹣2x+y的取值范围是　[﹣4，2]　．‎ ‎【考点】简单线性规划．‎ ‎【专题】数形结合；直线与圆．‎ ‎【分析】作出不等式组表示的平面区域；作出目标函数对应的直线；结合图象知当直线过A、B时，z最小、最大，从而得出目标函数z=﹣2x+y的取值范围．‎ ‎【解答】解：画出不等式表示的平面区域 将目标函数变形为z=﹣2x+y，作出目标函数对应的直线，‎ 直线过B（0，2）时，直线的纵截距最大，z最大，最大值为2；‎ 当直线过A（3，2）时，直线的纵截距最小，z最小，最小值为﹣4；‎ 则目标函数z=﹣2x+y的取值范围是[﹣4，2]．‎ 故答案为：[﹣4，2]．‎ ‎【点评】本题考查画不等式组表示的平面区域、考查数形结合求函数的最值．‎ ‎　‎ ‎9．（2013秋•南阳期中）已知x＞，则函数y=4x+的最小值为　7　．‎ ‎【考点】基本不等式在最值问题中的应用．‎ ‎【专题】计算题．‎ ‎【分析】先把函数整理成基本不等式的形式，进而求得函数的最小值．‎ ‎【解答】解：y=4x+=4x﹣5++5≥2+5=7‎ ‎∴函数y=4x+的最小值为7‎ 故答案为7‎ ‎【点评】本题主要考查了基本不等式在最值问题的应用．属基础题．‎ ‎　‎ ‎10．（2016秋•亭湖区校级期中）根据如图所示的伪代码，可知输出的结果T为　62250　．‎ ‎【考点】伪代码；循环结构．‎ ‎【专题】图表型．‎ ‎【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出满足条件T=2+4+6+8+…+498时，T的值．‎ ‎【解答】解：分析程序中各变量、各语句的作用，‎ 再根据流程图所示的顺序，可知：‎ 该程序的作用是累加并输出满足条件T=2+4+6+8+…+498值．‎ ‎∵T=2+4+6+8+…+498==62250，‎ 故输出的S值为62250．‎ 故答案为：62250．‎ ‎【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．‎ ‎　‎ ‎11．（2016秋•亭湖区校级期中）若a＜b＜0，则下列不等式中不成立的是　②　（只填序号）‎ ‎①＞‎ ‎②＞‎ ‎③|a|＞|b|‎ ‎④a2＞b2．‎ ‎【考点】不等式的基本性质．‎ ‎【专题】选作题；转化思想；演绎法；不等式．‎ ‎【分析】取a=﹣2，b=﹣1，代入验证可得结论．‎ ‎【解答】解：取a=﹣2，b=﹣1，则①＞成立；‎ ‎②＞不成立；‎ ‎③|a|＞|b|成立；‎ ‎④a2＞b2成立；‎ 故答案为②．‎ ‎【点评】本题主要考查不等式与不等关系，利用特殊值代入法，排除不符合条件的选项，是一种简单有效的方法．‎ ‎　‎ ‎12．（2014春•姜堰市校级期末）设A={x|x2﹣2x﹣3＞0}，B={x|x2+ax+b≤0}，若A∪B=R，A∩B=（3，4]，则a+b=　﹣7　．‎ ‎【考点】交、并、补集的混合运算；一元二次不等式的解法．‎ ‎【专题】不等式的解法及应用．‎ ‎【分析】解二次不等式可求出A，结合A∪B=R，A∩B=（3，4]，可得B=[﹣1，4]，即﹣1，4为方程x2+ax+b=0的两个根，由韦达定理可得a，b的值，进而求出答案．‎ ‎【解答】解：∵A={x|x2﹣2x﹣3＞0}={x|x＜﹣1或x＞3}=（﹣∞，﹣1）∪（3，+∞）‎ 又由A∪B=R，A∩B=（3，4]，‎ 故B=[﹣1，4]‎ 由B={x|x2+ax+b≤0}可得 ‎﹣1，4为方程x2+ax+b=0的两个根 由韦达定理得a=﹣3，b=﹣4‎ 故a+b=﹣7‎ 故答案为：﹣7‎ ‎【点评】本题考查的知识点是交，并集合运算，一元二次不等式的解法，方程与不等式式的关系，其中分析出﹣1，4为方程x2+ax+b=0的两个根，是解答的关键．‎ ‎　‎ ‎13．（2011•江苏模拟）如图是一个算法的流程图，若输出的结果是31，则判断框中的整数M的值是　4　．‎ ‎【考点】循环结构．‎ ‎【专题】常规题型．‎ ‎【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加S=1+21+22+23+24=31的值，并输出．‎ ‎【解答】解：程序在运行过程中各变量的值如下表示：‎ 是否继续循环 S A 循环前/1 1‎ 第一圈 是 1+21 2‎ 第二圈 是 1+21+22 3‎ 第三圈 是 1+21+22+23 4‎ 第四圈 是 1+21+22+23+24 5‎ ‎∵输出的结果是31‎ 故继续循环的条件A不能超过4‎ 故答案为：4．‎ ‎【点评】算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，属于基础题．‎ ‎　‎ ‎14．（2012•徐州模拟）已知正数x，y满足+=1，则x+y的最小值为　2+2　．‎ ‎【考点】基本不等式．‎ ‎【专题】不等式的解法及应用．‎ ‎【分析】变形利用“乘1法”和基本不等式的性质即可得出．‎ ‎【解答】解：∵正数x，y满足+=1，‎ 则x+y=（x+y+2）﹣2=2+=2+2，当且仅当x=1+=y时取等号．‎ ‎∴x+y的最小值为2+2．‎ 故答案为：2+2．‎ ‎【点评】本题考查了“乘1法”和基本不等式的性质，考查了变形的能力，考查了计算能力，属于中档题．‎ ‎　‎ 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15．（14分）（2016秋•亭湖区校级期中）已知二次函数f（x）=ax2﹣bx+2（a＞0）．‎ ‎（1）若不等式f（x）＞0的解集为{x|x＞2或x＜1}，求a和b的值；‎ ‎（2）若b=2a+1，解关于x的不等式f（x）≤0．‎ ‎【考点】二次函数的性质．‎ ‎【专题】计算题；分类讨论；转化思想；综合法；函数的性质及应用．‎ ‎【分析】（1）由题意，ax2﹣bx+2＞0（a＞0）的解集为{x|x＞2或x＜1}，根据不等式与方程的关系有：x1=2，x2=1求解a，b．‎ ‎（2）b=2a+1，那么：f（x）=ax2﹣（2a+1）x+2=（ax﹣2）（x﹣1）≤0．对a与1的大小比较近讨论，得解．‎ ‎【解答】解：（1）由题意，ax2﹣bx+2＞0（a＞0）的解集为{x|x＞2或x＜1}，根据不等式与方程的关系有：x1=2，x2=1，利用韦达定理：，，解得：a=1，b=3．‎ 故当不等式f（x）＞0的解集为{x|x＞2或x＜1}，a、b的值分别为1，3；‎ ‎（2）当b=2a+1，那么：f（x）=ax2﹣（2a+1）x+2=（ax﹣1）（x﹣2）‎ f（x）≤0，即（ax﹣1）（x﹣2）≤0，‎ 解得：x1=，x2=2．‎ 当0＜a＜时，x1＞x2，不等式的解集为[]‎ 当a=时，x1=x2，不等式的解集为{x|x=2}；‎ 当a＞时，x1＜x2，不等式的解集为[，2]；‎ 综上所述：当0＜a＜时，x1＞x2，不等式的解集为[]‎ 当a=时，x1=x2，不等式的解集为{x|x=2}；‎ 当a＞时，x1＜x2，不等式的解集为[，2]．‎ ‎【点评】本题主要考查了一元二次不等式的应用，以及根与系数的关系，同时考查了分析求解的能力和计算能力，属于中档题．‎ ‎　‎ ‎16．（14分）（2016秋•亭湖区校级期中）（1）若x＞﹣1，求y=的最小值；‎ ‎（2）若a，b，c都是正数，且a+b+c=1，求证（1﹣a）（1﹣b）（1﹣c）≥8abc．‎ ‎【考点】基本不等式；不等式的证明．‎ ‎【专题】函数思想；综合法；不等式．‎ ‎【分析】（1）x＞﹣1，可得x+1＞0．变形为函数y=（x+1）++5，利用基本不等式的性质即可得出．‎ ‎（2）根据已知条件知：1﹣a=b+c≥2；“=成立b=c”‎ ‎1﹣b=a+c≥2时取“=成立a=c“；‎ ‎1﹣c=a+b时取“=成立a=b“；‎ 所以这三个不等式两边同时相乘就可以得到要证的结论 ‎【解答】解：（1）∵x＞﹣1，∴x+1＞0．‎ ‎∴函数y==（x+1）++5≥2+5+5=4+5=9，‎ 当且仅当x+1=2，即x=1时取等号．‎ ‎∴函数y=的最小值；‎ ‎（x＞﹣1）的最小值为9；‎ ‎（2）证明：∵a+b+c=1，a，b，c都是正数；‎ ‎∴1﹣a=b+c≥2；“=成立b=c”‎ ‎1﹣b=a+c≥2时取“=成立a=c“；‎ ‎1﹣c=a+b时取“=成立a=b“；‎ ‎∴（1﹣a）（1﹣b）（1﹣c）≥8abc，a=b=c时取“=成立a=b=c= “；‎ ‎【点评】本题考查了函数的最小值、基本不等式的性质，考查了推理能力与计算能力，属于中档题 ‎　‎ ‎17．（14分）（2013•上海）甲厂以x千克/小时的速度匀速生产某种产品（生产条件要求1≤x≤10），每小时可获得的利润是100（5x+1﹣）元．‎ ‎（1）要使生产该产品2小时获得的利润不低于3000元，求x的取值范围；‎ ‎（2）要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求此最大利润．‎ ‎【考点】函数模型的选择与应用．‎ ‎【专题】应用题．‎ ‎【分析】（1）求出生产该产品2小时获得的利润，建立不等式，即可求x的取值范围；‎ ‎（2）确定生产900千克该产品获得的利润函数，利用配方法，可求最大利润．‎ ‎【解答】解：（1）生产该产品2小时获得的利润为100（5x+1﹣）×2=200（5x+1﹣）‎ 根据题意，200（5x+1﹣）≥3000，即5x2﹣14x﹣3≥0‎ ‎∴x≥3或x≤﹣‎ ‎∵1≤x≤10，∴3≤x≤10；‎ ‎（2）设利润为 y元，则生产900千克该产品获得的利润为y=100（5x+1﹣）×‎ ‎=90000（）=9×104[+]‎ ‎∵1≤x≤10，∴x=6时，取得最大利润为=457500元 故甲厂应以6千克/小时的速度生产，可获得最大利润为457500元．‎ ‎【点评】本题考查函数模型的建立，考查解不等式，考查函数的最值，确定函数的模型是关键．‎ ‎　‎ ‎18．（16分）（2016秋•亭湖区校级期中）如表给出了某校500名12岁男孩中用随机抽样得出的120人的身高（单位cm）．‎ ‎ 区间界限 ‎[122，126）‎ ‎[126，130）‎ ‎[130，134）‎ ‎[134，138）‎ ‎[138，142）‎ ‎[142，146）‎ 人数 ‎ ‎ 5‎ ‎8 ‎ ‎10 ‎ ‎ 22‎ ‎ 33‎ ‎20 ‎ ‎ 区间界限 ‎[146，150）‎ ‎[150，154）‎ ‎[154，158）‎ ‎ 人数 ‎ 11‎ ‎6 ‎ ‎ 5‎ ‎（1）列出样本频率分布表﹔‎ ‎（2）画出频率分布直方图﹔‎ ‎（3）估计身高小于134cm的人数占总人数的百分比．‎ ‎【考点】频率分布直方图．‎ ‎【专题】计算题；对应思想；定义法；概率与统计．‎ ‎【分析】根据样本频率分布表、频率分布直方图的一般步骤解题．‎ ‎【解答】解：（1）样本频率分布表如下：‎ 分组 频数 频率 ‎[122，126）‎ ‎5‎ ‎0.04‎ ‎[126，130）‎ ‎8‎ ‎0.07‎ ‎[130，134）‎ ‎10‎ ‎0.08‎ ‎[134，138）‎ ‎22‎ ‎0.18‎ ‎[138，142）‎ ‎33‎ ‎0.28‎ ‎[142，146）‎ ‎20‎ ‎0.17‎ ‎[146，150）‎ ‎11‎ ‎0.09‎ ‎[150，154）‎ ‎6‎ ‎0.05‎ ‎[154，158）‎ ‎5‎ ‎0.04‎ 合计 ‎120‎ ‎1‎ ‎（2）其频率分布直方图如下：‎ ‎（3）由样本频率分布表可知身高小于134 cm的男孩出现的频率为0.04+0.07+0.08=0.19，‎ 所以我们估计身高小于134 cm的人数占总人数的19%．‎ ‎【点评】本题考查频率分布表、频率分布图的作法，考查满足条件的百分比的求法，解题时要认真审题，是基础题．‎ ‎　‎ ‎19．（16分）（2016秋•亭湖区校级期中）设函数f（x）=mx2﹣mx﹣1（m≠0），若对于x∈[1，3]，f（x）＜﹣m+5恒成立，求m的取值范围．‎ ‎【考点】函数恒成立问题．‎ ‎【专题】计算题；转化思想；转化法；函数的性质及应用．‎ ‎【分析】由题意得m（x﹣）2+m﹣6＜0，x∈[1，3]恒成立，令g（x）=m（x﹣）2+m﹣6＜0，x∈[1，3]，利用函数的单调性质能求出m的取值范围．‎ ‎【解答】解：要x∈[1，3]，f（x）＜﹣m+5恒成立，‎ 即m（x﹣）2+m﹣6＜0，x∈[1，3]恒成立．‎ 令g（x）=m（x﹣）2+m﹣6＜0，x∈[1，3]，‎ 当 m＞0时，g（x）是增函数，‎ 所以g（x）max=g（3）=7m﹣6＜0，‎ 解得m＜．所以0＜m＜．‎ ‎∴m的取值范围是（0，）．‎ ‎【点评】本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意等价转化思想及函数性质的合理运用．‎ ‎　‎ ‎20．（16分）（2014春•姜堰市校级期末）已知集合A={x|x2﹣2x﹣3≤0}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}．‎ ‎（1）当m=2时，求A∪B；‎ ‎（2）若A∩B=[1，3]，求实数m的值；‎ ‎（3）若A⊆∁RB，求实数m的取值范围．‎ ‎【考点】集合的包含关系判断及应用．‎ ‎【专题】计算题；集合．‎ ‎【分析】（1）先求出集合A，B，可求A∪B；‎ ‎（2）利用A∩B=[1，3]，确定实数m的值．‎ ‎（3）求出∁RB，利用条件A⊆∁RB，确定条件关系，即可求实数m的取值范围．‎ ‎【解答】解：（1）∵A={x|x2﹣2x﹣3≤0，x∈R}，‎ ‎∴A={x|﹣1≤x≤3，x∈R}，‎ ‎∵B={x|x2﹣4x≤0}={x|0≤x≤4}，‎ ‎∴A∪B=[﹣1，4]；‎ ‎（2）∵A∩B=[1，3]，‎ ‎∴m﹣2=1，即m=3，‎ 此时B={x|1≤x≤5}，满足条件A∩B=[1，3]．‎ ‎（3）∵B={x|m﹣2≤x≤m+2}．‎ ‎∴∁RB={x|x＞m+2或x＜m﹣2}，‎ 要使A⊆∁RB，‎ 则3＜m﹣2或﹣1＞m+2，‎ 解得m＞5或m＜﹣3，‎ 即实数m的取值范围是m＞5或m＜﹣3．‎ ‎【点评】本题主要考查集合的基本运算，以及利用集合关系求参数问题，考查学生分析问题的能力．‎