2020届二轮复习函数的图象课件（32张）（全国通用）

2020届二轮复习函数的图象课件（32张）（全国通用）

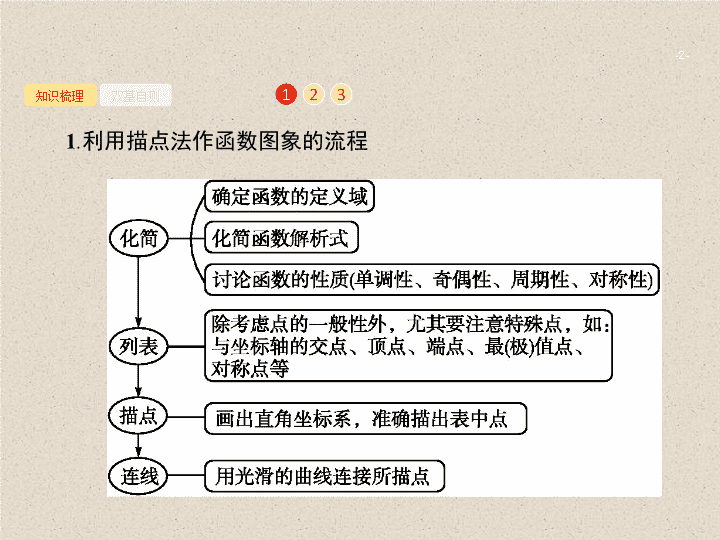
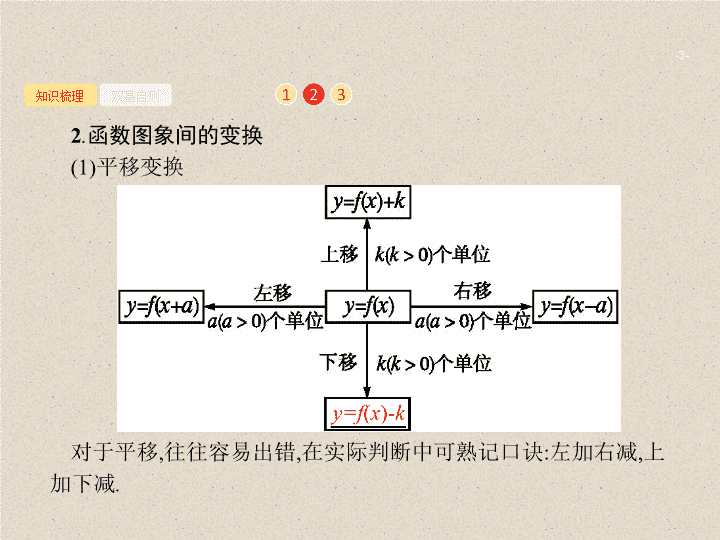
2 . 7 　 函数的图象 - 2 - 知识梳理 双基自测 2 3 1 1 . 利用描点法作函数图象的 流程 - 3 - 知识梳理 双基自测 2 3 1 2 . 函数图象间的变换 (1) 平移变换 对于平移 , 往往容易出错 , 在实际判断中可熟记口诀 : 左加右减 , 上加下减 . y=f ( x ) - k - 4 - 知识梳理 双基自测 2 3 1 (2) 对称变换 函数 y=-f ( -x ) 的 图象 - 5 - 知识梳理 双基自测 2 3 1 (3) 伸缩 变换 - 6 - 知识梳理 双基自测 2 3 1 3 . 有关对称性的常用结论 (1) 函数图象自身的轴对称 ① f ( -x ) =f ( x ) ⇔ 函数 y=f ( x ) 的图象关于 y 轴对称 ; ② 函数 y=f ( x ) 的图象关于 x=a 对称 ⇔ f ( a+x ) =f ( a-x ) ⇔ f ( x ) =f (2 a-x ) ⇔ f ( -x ) =f (2 a+x ); ③ 若函数 y=f ( x ) 的定义域为 R , 且有 f ( a+x ) =f ( b-x ), 则函数 y=f ( x ) 的 - 7 - 知识梳理 双基自测 2 3 1 (2) 函数图象自身的中心对称 ① f ( -x ) =-f ( x ) ⇔ 函数 y=f ( x ) 的图象关于原点对称 ; ② 函数 y=f ( x ) 的图象关于 ( a ,0) 对称 ⇔ f ( a+x ) =-f ( a-x ) ⇔ f ( x ) =-f (2 a-x ) ⇔ f ( -x ) =-f (2 a+x ); ③ 若函数 y=f ( x ) 的图象关于点 ( a , b ) 成中心对称 ⇔ f ( a+x ) = 2 b-f ( a-x ) ⇔ f ( x ) = 2 b-f (2 a-x ); ④ 若函数 y=f ( x ) 定义域为 R , 且满足条件 f ( a+x ) +f ( b-x ) =c ( a , b , c 为 - 8 - 知识梳理 双基自测 2 3 1 (3) 两个函数图象之间的对称关系 ① 函数 y=f ( a+x ) 与 y=f ( b-x ) 的图象关于直线 x = 对称 ; 函数 y=f ( x ) 与 y=f (2 a-x ) 的图象关于直线 x=a 对称 ; ② 函数 y=f ( x ) 与 y= 2 b-f ( -x ) 的图象关于点 (0, b ) 对称 ; ③ 函数 y=f ( x ) 与 y= 2 b-f (2 a-x ) 的图象关于点 ( a , b ) 对称 . 2 - 9 - 知识梳理 双基自测 3 4 1 1 . 下列结论正确的打 “ √ ”, 错误的打 “×” . (1) 将函数 y=f ( x ) 的图象先向左平移 1 个 单位 长度 , 再向下平移 1 个 单位 长度 得到 函数 y=f ( x+ 1) + 1 的图象 . ( 　　 ) (2) 当 x ∈ (0, +∞ ) 时 , 函数 y=|f ( x ) | 与 y=f ( |x| ) 的图象相同 . ( 　　 ) (3) 函数 y=f ( x ) 与 y=-f ( -x ) 的图象关于原点对称 . ( 　　 ) (4) 若函数 y=f ( x ) 满足 f (1 +x ) =f (1 -x ), 则函数 f ( x ) 的图象关于直线 x= 1 对称 . ( 　　 ) (5) 若函数 y=f ( x ) 满足 f ( x- 1) =f ( x+ 1), 则函数 f ( x ) 的图象关于直线 x= 1 对称 . ( 　　 ) 答案 答案 关闭 (1) × 　 (2) × 　 (3)√ 　 (4)√ 　 (5) × - 10 - 知识梳理 双基自测 2 3 4 1 2 . 已知函数 y= log a ( x+c )( a , c 为常数 , 其中 a> 0, a ≠1) 的图象如图 , 则下列结论成立的是 ( 　　 ) A. a> 1, c> 1 B. a> 1,0 1 D.0

查看更多