辽宁省抚顺市2020届高三下学期420模拟考试 数学(文)
2020年420模拟考试
数学试卷(文科)
考生注意:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分。考试时间120分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:高考全部内容。
第I卷
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
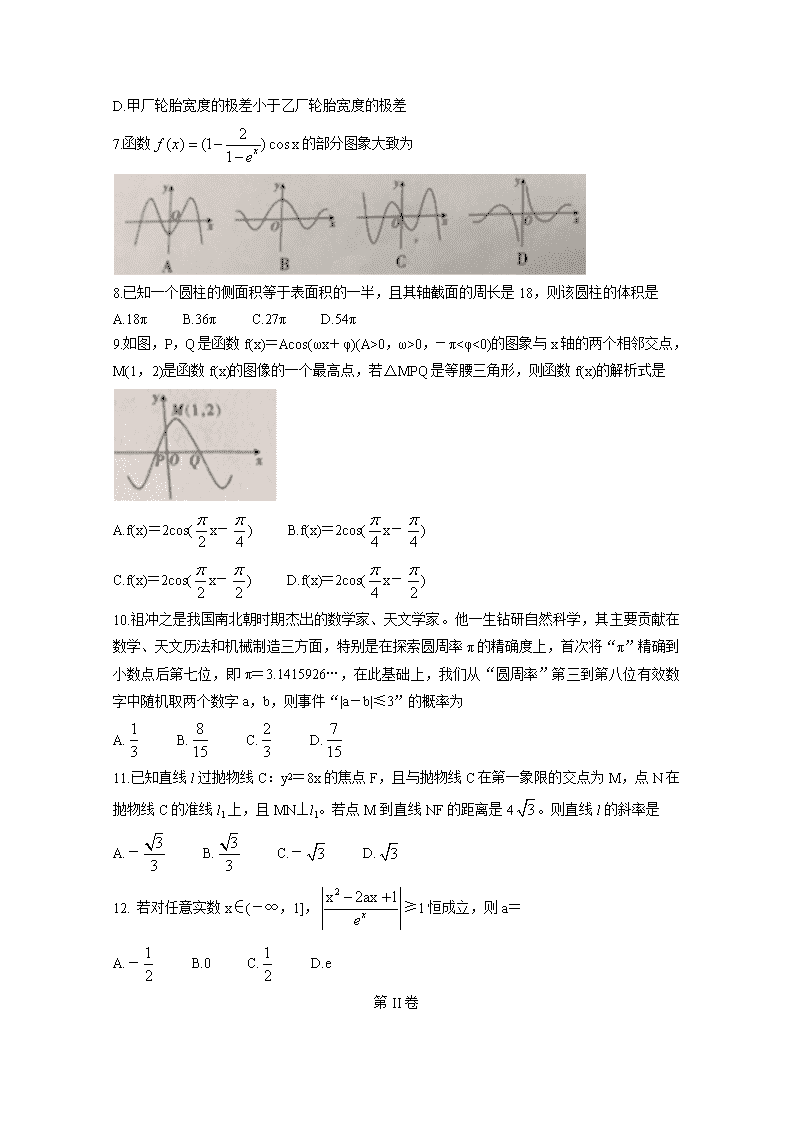
1.设集合A={-1,0,1,2,3},B={x|-3
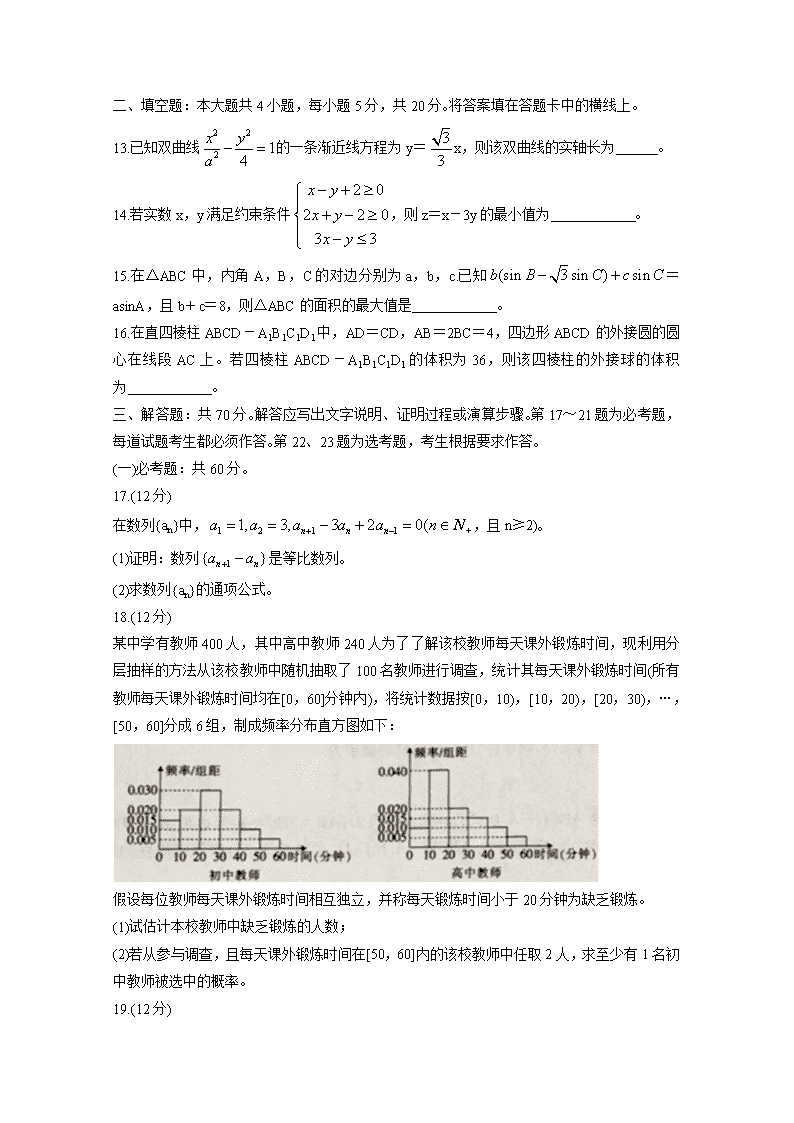
0,ω>0,-π<φ<0)的图象与x轴的两个相邻交点,M(1,2)是函数f(x)的图像的一个最高点,若△MPQ是等腰三角形,则函数f(x)的解析式是
A.f(x)=2cos(x-) B.f(x)=2cos(x-)
C.f(x)=2cos(x-) D.f(x)=2cos(x-)
10.祖冲之是我国南北朝时期杰出的数学家、天文学家。他一生钻研自然科学,其主要贡献在数学、天文历法和机械制造三方面,特别是在探索圆周率π的精确度上,首次将“π”精确到小数点后第七位,即π=3.1415926…,在此基础上,我们从“圆周率”第三到第八位有效数字中随机取两个数字a,b,则事件“|a-b|≤3”的概率为
A. B. C. D.
11.已知直线l过抛物线C:y2=8x的焦点F,且与抛物线C在第一象限的交点为M,点N在抛物线C的准线l1上,且MN⊥l1。若点M到直线NF的距离是4。则直线l的斜率是
A.- B. C.- D.
12. 若对任意实数x∈(-∞,1],≥1恒成立,则a=
A.- B.0 C. D.e
第II卷
二、填空题:本大题共4小题,每小题5分,共20分。将答案填在答题卡中的横线上。
13.已知双曲线的一条渐近线方程为y=x,则该双曲线的实轴长为 。
14.若实数x,y满足约束条件,则z=x-3y的最小值为 。
15.在△ABC中,内角A,B,C的对边分别为a,b,c.已知=asinA,且b+c=8,则△ABC的面积的最大值是 。
16.在直四棱柱ABCD-A1B1C1D1中,AD=CD,AB=2BC=4,四边形ABCD的外接圆的圆心在线段AC上。若四棱柱ABCD-A1B1C1D1的体积为36,则该四棱柱的外接球的体积为 。
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每道试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
在数列{an}中,,且n≥2)。
(1)证明:数列是等比数列。
(2)求数列{an}的通项公式。
18.(12分)
某中学有教师400人,其中高中教师240人为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在[0,60]分钟内),将统计数据按[0,10),[10,20),[20,30),…,[50,60]分成6组,制成频率分布直方图如下:
假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼。
(1)试估计本校教师中缺乏锻炼的人数;
(2)若从参与调查,且每天课外锻炼时间在[50,60]内的该校教师中任取2人,求至少有1名初中教师被选中的概率。
19.(12分)
如图1,在梯形ABCD中,AB//CD,且AB=2CD,△ABC是等腰直角三角形,其中BC为斜边,若把△ACD沿AC边折叠到△ACP的位置,使平面PAC⊥平面ABC,如图2。
(1)证明:AB⊥PA。
(2)若E为棱BC的中点,求点B到平面PAE的距离。
20.(12分)
已知函数。
(1)讨论f(x)的单调性;
(2)讨论f(x)在(0,+∞)上的零点个数。
21.(12分)
已知椭圆C:的离心率为,且四个顶点构成的四边形的面积是。
(1)求椭圆C的方程;
(2)已知直线l经过点P(-2,0),且不垂直于y轴,直线l与椭圆C交于A,B两点,M为AB的中点,直线OM与椭圆C交于E,F两点(O是坐标原点),若四边形AEBF的面积为,求直线l的方程。
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy中,曲线C的参数方程为(α为参数)。以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为。
(1)求C与l的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,点P(-2,2),求的值。
23.[选修4-5:不等式选讲](10分)
已知函数f(x)=|x+a|+|x-5|。
(1)当a=3时,求不等式f(x)≤10的解集;
(2)若f(x)≥1,求a的取值范围。