2019届二轮复习对数与对数函数学案（全国通用）

2019届二轮复习对数与对数函数学案（全国通用）

‎2019届二轮复习 对数与对数函数 学案 （全国通用）‎ ‎1.理解对数的概念及其运算性质，知道用换底公式将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用；‎ ‎2.理解对数函数的概念及其单调性，掌握对数函数图象通过的特殊点，会画底数为2，10，的对数函数的图象；‎ ‎3.体会对数函数是一类重要的函数模型.‎ ‎4.了解指数函数y＝ax(a>0，且a≠1)与对数函数y＝logax(a>0，且a≠1)互为反函数．‎ ‎ ‎ ‎1．对数的概念 一般地，对于指数式ab＝N，我们把“以a为底N的对数b”记作logaN，即b＝logaN(a>0，且a≠1)．其中，数a叫做对数的底数，N叫做真数，读作“b等于以a为底N的对数”．‎ ‎2．对数的性质与运算法则 ‎(1)对数的运算法则 如果a>0且a≠1，M>0，N>0，那么 ‎①loga(MN)＝logaM＋logaN；②loga＝logaM－logaN；‎ ‎③logaMn＝nlogaM (n∈R)；④logamMn＝logaM.‎ ‎(2)对数的性质 ‎①alogaN＝ N ；②logaaN＝ N (a>0且a≠1)．‎ ‎(3)对数的重要公式 ‎①换底公式：logbN＝ (a，b均大于零且不等于1)；‎ ‎②logab＝，推广logab·logbc·logcd＝logad.‎ ‎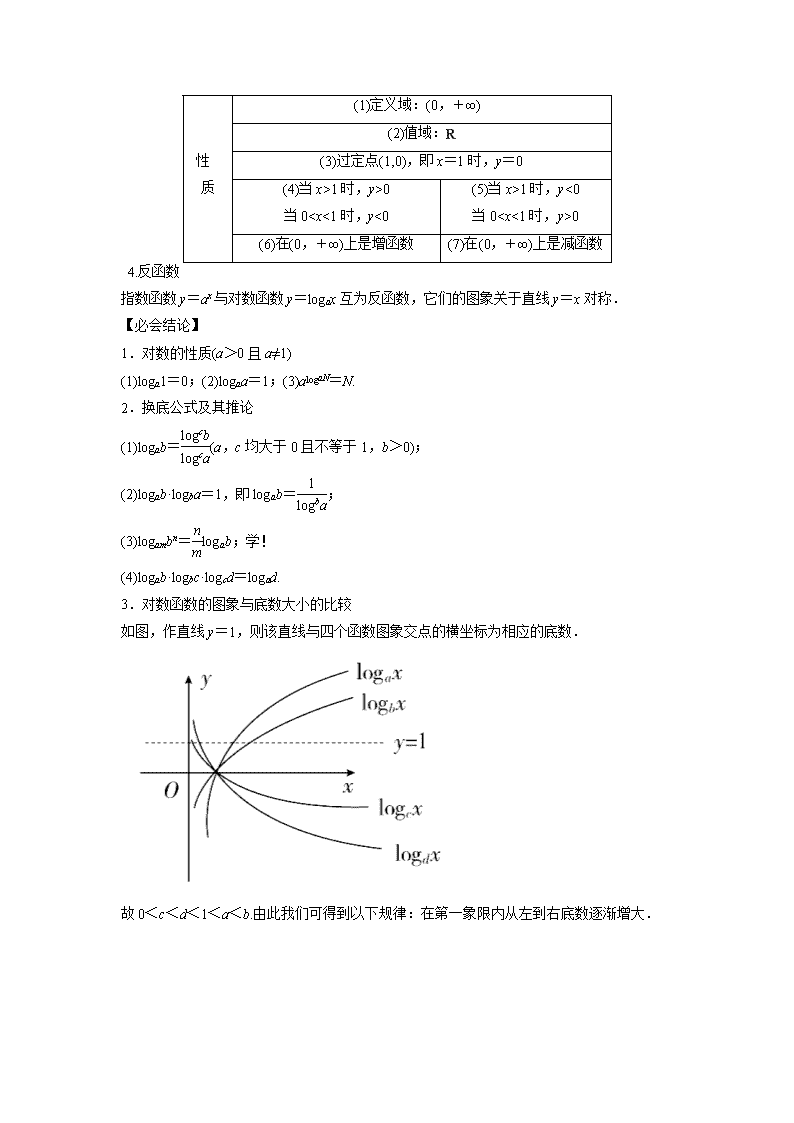3．对数函数的图象与性质 a>1‎ ‎01时，y>0‎ 当01时，y<0‎ 当00‎ ‎(6)在(0，＋∞)上是增函数 ‎(7)在(0，＋∞)上是减函数 ‎4.反函数 指数函数y＝ax与对数函数y＝logax互为反函数，它们的图象关于直线y＝x对称．‎ ‎【必会结论】‎ ‎1．对数的性质(a＞0且a≠1)‎ ‎(1)loga1＝0；(2)logaa＝1；(3)alogaN＝N.‎ ‎2．换底公式及其推论 ‎(1)logab＝(a，c均大于0且不等于1，b＞0)；‎ ‎(2)logab·logba＝1，即logab＝；‎ ‎(3)logambn＝logab；学！ ‎ ‎(4)logab·logbc·logcd＝logad.‎ ‎3．对数函数的图象与底数大小的比较 如图，作直线y＝1，则该直线与四个函数图象交点的横坐标为相应的底数．‎ 故0＜c＜d＜1＜a＜b.由此我们可得到以下规律：在第一象限内从左到右底数逐渐增大．‎ 高频考点一　对数式的运算 例1、(1)lg 52＋lg 8＋lg 5·lg 20＋(lg 2)2的值为 ．‎ 答案　3‎ 解析　原式＝2lg 5＋2lg 2＋lg 5(1＋lg 2)＋lg2 2＝2(lg 5＋lg 2)＋lg 5＋lg 2(lg 2＋lg 5)＝2＋lg 5＋lg 2＝3.‎ ‎(2)已知3a＝4b＝，则＋＝ .‎ 答案　2‎ 解析　因为3a＝4b＝，所以a＝log3，‎ b＝log4，＝log3，＝log4，‎ 所以＋＝log3＋log4＝log12＝2.‎ ‎ 【变式探究】(1)设2a＝5b＝m，且＋＝2，则m等于(　　)‎ A. B．10 C．20 D．100‎ ‎(2)计算：÷100－＝ ．‎ ‎【方法规律】对数运算的一般思路 ‎(1)将真数化为底数的指数幂的形式进行化简；‎ ‎(2)将同底对数的和、差、倍合并；‎ ‎(3)利用换底公式将不同底的对数式转化成同底的对数式，要注意换底公式的正用、逆用及变形应用．‎ ‎【变式探究】 (1)已知函数f(x)＝则f(2＋log23)的值为(　　)‎ A．24 B．16 C．12 D．8‎ ‎(2) lg＋2lg 2－＝ ．‎ 解析　(1)因为3<2＋log23<4，所以f(2＋log23)＝f(3＋log23)＝23＋log23＝8×2log23＝24.‎ ‎(2)lg＋2lg 2－＝lg 5－lg 2＋2lg 2－2＝lg 5＋lg 2－2＝lg 10－2＝－1.‎ 答案　(1)A　(2)－1‎ 高频考点二　对数函数的图象及应用 例2、(1)若函数y＝a|x|(a>0，且a≠1)的值域为{y|y≥1}，则函数y＝loga|x|的图象大致是(　　)‎ ‎(2)已知函数f(x)＝且关于x的方程f(x)＋x－a＝0有且只有一个实根，则实数a的取值范围是 ．‎ 解析　(1)由于y＝a|x|的值域为{y|y≥1}，‎ ‎∴a>1，则y＝logax在(0，＋∞)上是增函数，‎ 又函数y＝loga|x|的图象关于y轴对称．‎ 因此y＝loga|x|的图象应大致为选项B.‎ ‎(2)如图，在同一坐标系中分别作出y＝f(x)与y＝－x＋a的图象，其中a表示直线在y轴上截距．‎ 由图可知，当a>1时，直线y＝－x＋a与y＝log2x只有一个交点．‎ 答案　(1)B　(2) a>1‎ ‎【方法规律】应用对数型函数的图象可求解的问题 ‎(1)对一些可通过平移、对称变换作出其图象的对数型函数，在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合思想．‎ ‎(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．‎ ‎【变式探究】 (1)函数y＝2log4(1－x)的图象大致是(　　)‎ ‎(2)当01时，不符合题意，舍去．‎ 所以实数a的取值范围是.‎ 答案　(1)C　(2)B 高频考点三　对数函数的性质及应用 例3、(2016·全国Ⅰ卷)若a>b>0，0cb 解析　由y＝xc与y＝cx的单调性知，C、D不正确．‎ ‎∵y＝logcx是减函数，得logca0且a≠1，设t(x)＝3－ax，‎ 则t(x)＝3－ax为减函数，‎ x∈[0，2]时，t(x)的最小值为3－2a，‎ 当x∈[0，2]时，f(x)恒有意义，‎ 即x∈[0，2]时，3－ax>0恒成立．‎ ‎∴3－2a>0.∴a<.又a>0且a≠1，∴a∈(0，1)∪.‎ ‎(2)t(x)＝3－ax，∵a>0，‎ ‎∴函数t(x)为减函数．‎ ‎∵f(x)在区间[1，2]上为减函数，∴y＝logat为增函数，‎ ‎∴a>1，x∈[1，2]时，t(x)最小值为3－2a，f(x)最大值为f(1)＝loga(3－a)，‎ ‎∴即 故不存在这样的实数a，使得函数f(x)在区间[1，2]上为减函数，并且最大值为1.‎ 高频考点四 和对数函数有关的复合函数 例4、已知函数f(x)＝loga(3－ax)．‎ ‎(1)当x∈[0,2]时，函数f(x)恒有意义，求实数a的取值范围；‎ ‎(2)是否存在这样的实数a，使得函数f(x)在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由．‎ 解　(1)∵a>0且a≠1，设t(x)＝3－ax，‎ 则t(x)＝3－ax为减函数，‎ x∈[0,2]时，t(x)的最小值为3－2a，‎ 当x∈[0,2]时，f(x)恒有意义，‎ 即x∈[0,2]时，3－ax>0恒成立．‎ ‎∴3－2a>0.∴a<.‎ 又a>0且a≠1，∴a∈(0,1)∪.‎ ‎【感悟提升】在解决与对数函数相关的比较大小或解不等式问题时，要优先考虑利用对数函数的单调性来求解．在利用单调性时，一定要明确底数a的取值对函数增减性的影响，及真数必须为正的限制条件．‎ ‎【变式探究】(1)设a＝log32，b＝log52，c＝log23，则(　　)‎ A．a>c>b B．b>c>a C．c>b>a D．c>a>b ‎(2)若f(x)＝lg(x2－2ax＋1＋a)在区间(－∞，1]上递减，则a的取值范围为(　　)‎ A． [1,2) B．[1,2]‎ C．[1，＋∞) D．[2，＋∞)‎ ‎(3)设函数f(x)＝若f(a)>f(－a)，则实数a的取值范围是(　　)‎ A．(－1,0)∪(0,1) B．(－∞，－1)∪(1，＋∞)‎ C．(－1,0)∪(1，＋∞) D．(－∞，－1)∪(0,1)‎ 答案　(1)D　(2)A　(3)C 解析　(1)∵<2<3,1<2<，3>2，‎ ‎∴log3log22，‎ ‎∴1，∴c>a>b.‎ ‎(2)令函数g(x)＝x2－2ax＋1＋a＝(x－a)2＋1＋a－a2，对称轴为x＝a，要使函数在(－∞，1]上递减，则有即 解得1≤a<2，即a∈[1,2)，故选A.学 ！ ‎ ‎(3)由题意可得或 解得a>1或－10时，f(x)>f(0)＝0，且f′(x)>0，‎ g(x)＝xf(x)，则g′(x)＝f(x)＋xf′(x)>0，∴g(x)在[0，＋∞)上递增．‎ a＝g(－log25.1)＝g(log25.1)，由对数函数y＝log2x的性质，知3＝log28>log25.1>log24＝2>20.8，∴c>a>b.故选C.‎ ‎ 【变式探究】(1)设a＝0.50.5，b＝0.30.5，c＝log0.30.2，则a，b，c的大小关系是(　　)‎ A．cb>c B．b>a>c C．a>c>b D．c>b>a ‎(3)已知，则(　　)‎ A．a>b>c B．b>a>c C．a>c>b D．c>a>b 解析　(1)根据幂函数y＝x0.5的单调性，‎ 可得0.30.5<0.50.5<10.5＝1，即blog0.30.3＝1，即c>1.‎ 所以blog22＝1，b＝logπ＝log2log3>log43.6.‎ 方法二　∵log3>log33＝1，且<3.4，‎ ‎∴log31，‎ ‎∴log43.6log3>log43.6.‎ 由于y＝5x为增函数，∴5>>5.‎ 即5>>5，故a>c>b.‎ 答案　(1)C　(2)C　(3)C ‎【感悟提升】(1)比较指数式和对数式的大小，可以利用函数的单调性，引入中间量；有时也可用数形结合的方法．‎ ‎(2)解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1.‎ 高频考点六 有关对数运算的创新应用问题 例6、[2017·北京高考]根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(　　)‎ ‎(参考数据：lg 3≈0.48)‎ A．1033 B．1053 C．1073 D．1093‎ ‎【感悟提升】在解决对数的化简与求值问题时，要理解并灵活运用对数的定义、对数的运算性质、对数恒等式和对数的换底公式，同时还要注意化简过程中的等价性和对数式与指数式的互化.‎ ‎【变式探究】里氏震级M的计算公式为M＝lg A－lg A0，其中A是测震仪记录的地震曲线的最大振幅，A0是相应的标准地震的振幅．假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅为0.001，则此次地震的震级为 级；9级地震的最大振幅是5级地震的最大振幅的 倍．‎ 答案　6　10000‎ 解析　根据题意，由lg 1000－lg 0.001＝6得此次地震的震级为6级．因为标准地震的振幅为0.001，设9级地震的最大振幅为A9，则lg A9－lg 0.001＝9，解得A9＝106，同理5级地震的最大振幅A5＝102，所以9级地震的最大振幅是5级地震的最大振幅的10000倍．‎ ‎1. （2018年天津卷）已知，，，则a，b，c的大小关系为 A. B. C. D. ‎ ‎【答案】D ‎【解析】由题意结合对数函数的性质可知：‎ ‎，，，‎ 据此可得：.，本题选择D选项.‎ ‎2. （2018年天津卷）已知函数，，其中a>1.‎ ‎（I）求函数的单调区间；‎ ‎（II）若曲线在点处的切线与曲线在点 处的切线平行，证明；‎ ‎（III）证明当时，存在直线l，使l是曲线的切线，也是曲线的切线.‎ ‎【答案】(Ⅰ)单调递减区间，单调递增区间为；(Ⅱ)证明见解析；(Ⅲ)证明见解析.‎ ‎【解析】（I）由已知，，有.‎ 令，解得x=0.‎ 由a>1，可知当x变化时，，的变化情况如下表：‎ x ‎0‎ ‎0‎ ‎+‎ 极小值 所以函数的单调递减区间为，单调递增区间为.‎ ‎（II）由，可得曲线在点处的切线斜率为.‎ 由，可得曲线在点处的切线斜率为.‎ 因为这两条切线平行，故有，即.‎ 两边取以a为底的对数，得，所以.‎ ‎（III）曲线在点处的切线l1：.‎ 曲线在点处的切线l2：.‎ 要证明当时，存在直线l，使l是曲线的切线，也是曲线的切线，‎ 只需证明当时，存在，，使得l1和l2重合.‎ 即只需证明当时，方程组有解，‎ 由①得，代入②，得. ③‎ 因此，只需证明当时，关于x1的方程③存在实数解.‎ 设函数，‎ 即要证明当时，函数存在零点.‎ ‎，可知时，；‎ 时，单调递减，‎ 又，，‎ 故存在唯一的x0，且x0>0，使得，即.‎ 由此可得在上单调递增，在上单调递减. ‎ 在处取得极大值.‎ 因为，故，‎ 所以.‎ 下面证明存在实数t，使得.‎ 由（I）可得，‎ 当时，有 ‎，‎ 所以存在实数t，使得 因此，当时，存在，使得.‎ 所以，当时，存在直线l，使l是曲线的切线，也是曲线的切线.‎ ‎1、[2017·北京高考]根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(　　)‎ ‎(参考数据：lg 3≈0.48)‎ A．1033 B．1053 C．1073 D．1093‎ 解析　由题意，lg＝lg＝lg 3361－lg 1080‎ ‎＝361lg 3－80lg 10≈361×0.48－80×1＝93.28.‎ 又lg 1033＝33，lg 1053＝53，lg 1073＝73，lg 1093＝93，‎ 故与最接近的是1093.故选D.‎ 答案　D ‎2、[2017·天津高考]已知奇函数f(x)在R上是增函数，g(x)＝xf(x)．若a＝g(－log25.1)，b＝g(20.8)，c＝g(3)，则a，b，c的大小关系为(　　)‎ A．a＜b＜c B．c＜b＜a C．b＜a＜c D．b＜c＜a 答案　C 解析　∵f(x)是奇函数，∴f(－x)＝－f(x)，‎ ‎∴g(－x)＝－xf(－x)＝xf(x)＝g(x)，g(x)为偶函数．‎ 又f(x)在R上递增，当x>0时，f(x)>f(0)＝0，且f′(x)>0，‎ g(x)＝xf(x)，则g′(x)＝f(x)＋xf′(x)>0，∴g(x)在[0，＋∞)上递增．‎ a＝g(－log25.1)＝g(log25.1)，由对数函数y＝log2x的性质，知3＝log28>log25.1>log24＝2>20.8，∴c>a>b.故选C.‎ ‎1、【2016·浙江卷】已知a>b>1，若logab＋logba＝，ab＝ba，则a＝ ，b＝ ．‎ ‎2、(2016·全国Ⅰ卷)若a>b>0，0cb 解析　由y＝xc与y＝cx的单调性知，C、D不正确．‎ ‎∵y＝logcx是减函数，得logca0，且a≠1)的图像如图11所示，则下列函数图像正确的是(　　)‎ 图11‎ ‎ A　　　　　　　　　　　B ‎　　　　C　　　　　　　　　　　D ‎【答案】B　‎ ‎【解析】由函数y＝logax的图像过点(3，1)，得a＝3.选项A中的函数为y＝，则其函数图像不正确；选项B中的函数为y＝x3，则其函数图像正确；选项C中的函数为y＝(－x)3，则其函数图像不正确；选项D中的函数为y＝log3(－x)，则其函数图像不正确．‎ ‎（2014·广东卷）若等比数列{an}的各项均为正数，且a‎10a11＋a‎9a12＝2e5，则ln a1＋ln a2＋…＋ln a20＝ ．‎ ‎【答案】50　‎ ‎（2014·辽宁卷）已知a＝2－，b＝log2，‎ c＝log，则(　　)‎ A．a>b>c B．a>c>b ‎ C．c>a>b D．c>b>a ‎【答案】C　‎ ‎【解析】因为0log＝1，所以c>a>b.‎ ‎（2014·天津卷）函数f(x)＝log(x2－4)的单调递增区间为(　　)‎ A．(0，＋∞) ‎ B．(－∞，0) ‎ C．(2，＋∞) ‎ D．(－∞，－2)‎ ‎【答案】D　‎ ‎【解析】要使f(x)单调递增，需有解得x<－2.‎ ‎（2014·浙江卷）在同一直角坐标系中，函数f(x)＝xa(x>0)，g(x)＝logax的图像可能是(　　)‎ ‎　 　　A　　　　　　　　　　　　B ‎　 　　C　　　　　　　　　　　　D ‎【答案】D　‎ ‎【解析】只有选项D符合，此时0，则f(10x)>0的解集为(　　)‎ A．{x|x<－1或x>－lg 2} ‎ B．{x|－1－lg 2} ‎ D．{x|x<－lg 2}‎ ‎【答案】D　‎ ‎【解析】根据已知可得不等式f(x)>0的解是－10，b>0，则ln＋(ab)＝bln＋a；‎ ‎②若a>0，b>0，则ln＋(ab)＝ln＋a＋ln＋b；‎ ‎③若a>0，b>0，则ln＋≥ln＋a－ln＋b；‎ ‎④若a>0，b>0，则ln＋(a＋b)≤ln＋a＋ln＋b＋ln 2.‎ 其中的真命题有 ．(写出所有真命题的编号)‎ ‎【答案】①③④　‎ ‎【解析】①中，当ab≥1时，∵b>0，∴a≥1，ln＋(ab)＝ln ab＝bln a＝bln＋a；当00，∴01时，左边＝ln＋(ab)＝0，右边＝ln＋a＋ln＋b＝ln a＋0＝ln a>0，∴②不成立；‎ ‎③中，当≤1，即a≤b时，左边＝0，右边＝ln＋a－ln＋b≤0，左边≥右边成立；当>1时，左边＝ln＝ln a－ln b>0，若a>b>1时，右边＝ln a－ln b，左边≥右边成立；若01>b>0，左边＝ln＝ln a－ln b>ln a，右边＝ln a，左边≥右边成立，∴③正确；‎ ‎④中，若00，左边≤右边；若a＋b≥1，ln＋－ln 2＝ln－ln 2＝ln，‎ 又∵≤a或≤b，a，b至少有1个大于1，∴ln≤ln a或ln≤ln b，即有ln＋－ln 2＝ln－‎ ln 2＝ln≤ln＋a＋ln＋b，∴④正确．‎ ‎（2013·新课标全国卷Ⅱ] 设a＝log36，b＝log510，c＝log714，则(　　)‎ A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c ‎【答案】D　‎ ‎【解析】a－b＝log36－log510＝(1＋log32)－(1＋log52)＝log32－log52>0，‎ b－c＝log510－log714＝(1＋log52)－(1＋log72)＝log52－log72>0，‎ 所以a>b>c，选D.学 ‎ ‎（2013·浙江卷）已知x，y为正实数，则(　　)‎ A．2lg x＋lg y＝2lg x＋2lg y B．2lg(x＋y)＝2lg x·2lg y C．2lg x·lg y＝2lg x＋2lg y D．2lg(xy)＝2lg x·2lg y ‎【答案】D　‎ ‎【解析】∵lg(xy)＝lg x＋lg y，∴2lg(xy)＝2lg x＋lg y＝2lgx2lgy，故选择D.‎ ‎ ‎