2018-2019学年甘肃省兰州一中高二下学期期末考试数学(理)试题 word版
兰州一中2018-2019-2学期高二年级期末考试试题
数 学(理科)
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。答案写在答题卡上,交卷时只交答题卡。
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b组成复数a+bi,其中虚数的个数是 ( )
A.30 B.42 C.36 D.35
2.不等式|x-5|+|x+3|≥6的解集是 ( )
A.[-5,7] B. (-∞,+∞)
C.(-∞,-5]∪[7,+∞) D. [-4,6]
3.甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性做试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表:
甲
乙
丙
丁
r
0.82
0.78
0.69
0.85
m
106
115
124
103
则哪位同学的试验结果体现A,B两变量有更强的线性相关性 ( )
A.甲 B.乙 C.丙 D.丁
4.的展开式中x4的系数为 ( )
A. 80 B. 40 C. 20 D. 10
5.下列四个不等式:①logx10+lgx≥2(x>1);②|a-b|<|a|+|b|;③≥2(ab≠0);④|x-1|+|x-2|≥1,其中恒成立的个数是 ( )
A.1 B.2 C.3 D.4
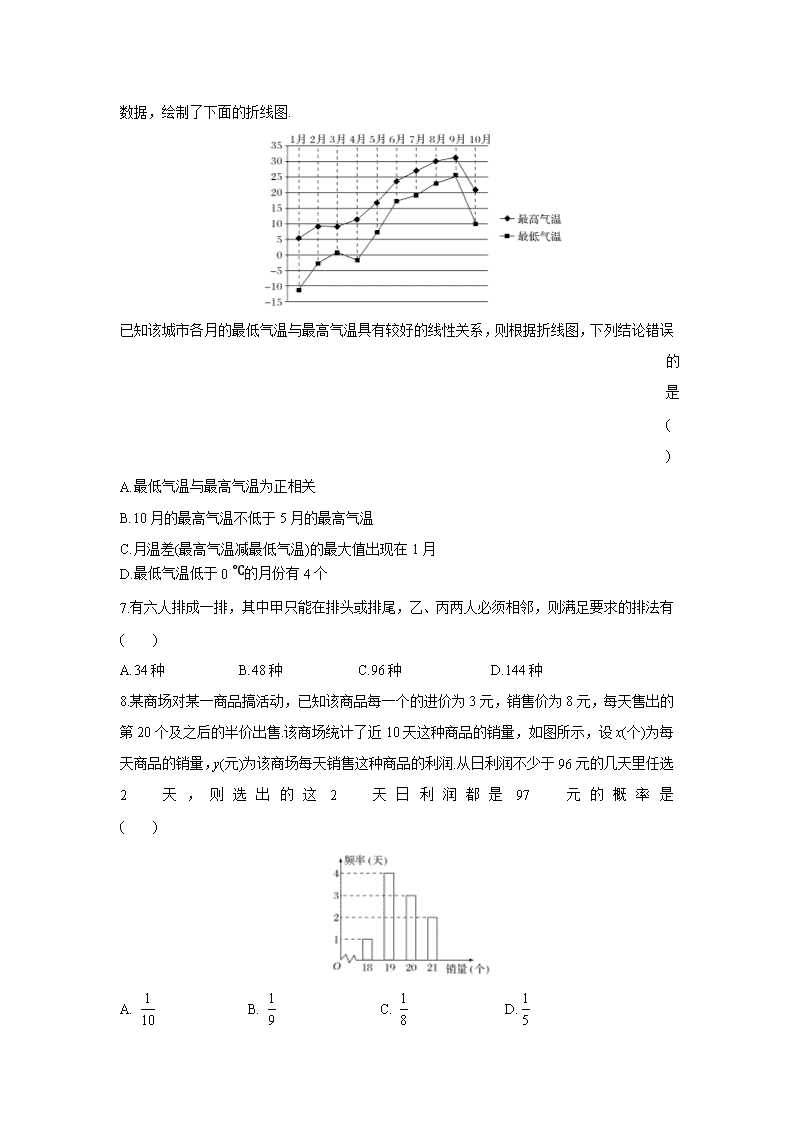
6.
某城市收集并整理了该市2018年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.
已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论错误的是( )
A.最低气温与最高气温为正相关
B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于0 ℃的月份有4个
7.有六人排成一排,其中甲只能在排头或排尾,乙、丙两人必须相邻,则满足要求的排法有( )
A.34种 B.48种 C.96种 D.144种
8.某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天这种商品的销量,如图所示,设x(个)为每天商品的销量,y(元)为该商场每天销售这种商品的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率是 ( )
A. B. C. D.
9.若对于实数x,y有|1-x|≤2,|y+1|≤1,则|2x+3y+1|的最大值是 ( )
A.5 B.6 C.7 D.8
10.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,D(X)=2.4,P(X=4)
ax-1.
(1)当a=1时,求不等式的解集;
(2)若不等式的解集为R,求a的取值范围.
18.(本小题满分12分)
已知函数f(x)=|2x-3|+|2x-1|的最小值为M.
(1)若m,n∈[-M,M],求证:2|m+n|≤|4+mn|;
(2)若a,b∈(0,+∞),a+2b=M,求+的最小值.
19.(本小题满分12分)
某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底
余额),如下表1:
年份x
2013
2014
2015
2016
2017
储蓄存款y(千亿元)
5
6
7
8
10
表1
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x-2 012,z=y-5得到下表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
表2
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2022年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程=x+,其中=,=-)
20.(本小题满分12分)
甲、乙两班进行“一带一路”知识竞赛,每班出3人组成甲、乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错或不答都得0分,已知甲队3人每人答对的概率分别为,,,乙队每人答对的概率都是,设每人回答正确与否相互之间没有影响,用ξ表示甲队总得分.
(1)求ξ=2的概率;
(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
21. (本小题满分12分)
某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大?
22.(本小题满分12分)
环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数PM2.5浓度,制定了空气质量标准:
空气污染指数
(0,50]
(50,100]
(100,150]
(150,200]
(200,300]
(300,+∞)
空气质量等级
优
良
轻度污染
中度污染
重度污染
严重污染
某市政府为了打造美丽城市,节能减排,从2010年开始考察了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号是字母的,前13个视为单号,后13个视为双号).王先生有一辆车,若11月份被限行的概率为0.05.
(1)求频率分布直方图中m的值;
(2)若按分层抽样的方法,从空气质量等级为良与中度污染的天气中抽取6天,再从这6天中随机抽取2天,求至少有一天空气质量是中度污染的概率;
(3)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行两年来的11月份共60天的空气质量进行统计,其结果如下表:
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
天数
11
27
11
7
3
1
根据限行前6年180天与限行后60天的数据,计算并填写2×2列联表,并回答是否有90%的把握认为空气质量的优良与汽车尾气的排放有关.
空气质量优、良
空气质量污染
总计
限行前
限行后
总计
参考数据:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
k0
2.072
2.706
3.841
5.024
6.635
7.879
参考公式:,其中.
兰州一中2018-2019-2学期期末考试
高二理科数学试题参考答案
一、选择题(本题共12小题,每小题5分,共60分。)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
D
B
C
D
C
A
C
B
D
A
二、填空题(本大题共4小题,每小题5分,共20分)
13. 14. 15. 16.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
解:(1)令f(x)=|2x-5|+|2x+1|,
则f(x)=|2x-5|+|2x+1|=
因为a=1,所以当x≤-时,由-4x+4>x-1,解得x≤-,
当-<x≤时,由6>x-1,解得-<x≤,
当x>时,由4x-4>x-1,解得x>.
综上得,所求不等式的解集为R. …………5分
(2)由(1)作函数f(x)的图象,点A,令y=ax-1,则其过定点P(0,-1),如图所示,由不等式|2x-5|+|2x+1|>ax-1的解集为R,可得
-4≤a<,即-4≤a<.所以,所求实数a的取值范围为.
…………10分
18.(本小题满分12分)
(1)证明 ∵f(x)=|2x-3|+|2x-1|≥|2x-3-(2x-1)|=2,∴M=2.
要证明2|m+n|≤|4+mn|,
只需证明4(m+n)2≤(4+mn)2,
∵4(m+n)2-(4+mn)2=4(m2+2mn+n2)-(16+8mn+m2n2)=(m2-4)(4-n2),
∵m,n∈[-2,2],∴m2,n2∈[0,4],
∴(m2-4)(4-n2)≤0,
∴4(m+n)2-(4+mn)2≤0,
∴4(m+n)2≤(4+mn)2,可得2|m+n|≤|4+mn|. …………6分
(2)解:由(1)得,a+2b=2,
因为a,b∈(0,+∞),
所以+=(a+2b)
=≥=4,
当且仅当a=1,b=时,等号成立.
所以+的最小值为4. …………12分
19.(本小题满分12分)
解(1)=3,=2.2,tizi=45,t=55,
==1.2, …………3分
=-=2.2-3×1.2=-1.4,
所以=1.2t-1.4. …………6分
(2)将t=x-2 012,z=y-5,代入=1.2t-1.4,
得y-5=1.2(x-2 012)-1.4,即=1.2x-2 410.8. …………9分
(3)因为=1.2×2 022-2 410.8=15.6,
所以预测到2022年年底,该地储蓄存款额可达15.6千亿元. …………12分
20.(本小题满分12分)
解(1)ξ=2,则甲队有两人答对,一人答错,
故P(ξ=2)=××+××+××= .…………4分
(2)设甲队和乙队得分之和为4为事件A,甲队比乙队得分高为事件B.设乙队得分为η,则η~B. .…………5分
P(ξ=1)=××+××+××=,
P(ξ=3)=××=,
P(η=1)=C·×=,
P(η=2)=C·×=,
P(η=3)=C=, .…………7分
∴P(A)=P(ξ=1)P(η=3)+P(ξ=2)P(η=2)+P(ξ=3)·P(η=1)
=×+×+×=, .…………9分
P(AB)=P(ξ=3)·P(η=1)=×=, .…………10分
∴所求概率为P(B|A)===. …………12分
21.(本小题满分12分)
解 (1)设甲正确完成面试的题数为ξ,则ξ的可能取值为1,2,3.
P(ξ=1)==;
P(ξ=2)==;
P(ξ=3)==.
应聘者甲正确完成题数ξ的分布列为
ξ
1
2
3
P
.…………3分
E(ξ)=1×+2×+3×=2. .…………4分
设乙正确完成面试的题数为η,则η的可能取值为0,1,2,3.
P(η=0)=C=;
P(η=1)=C=;
P(η=2)=C=;
P(η=3)=C=.
应聘者乙正确完成题数η的分布列为
η
0
1
2
3
P
.…………7分
E(η)=0×+1×+2×+3×=2.
(或因为η~B,所以E(η)=3×=2) .…………8分
(2)因为D(ξ)=(1-2)2×+(2-2)2×+(3-2)2×=,D(η)=3××=.
所以D(ξ)2.706,
所以有90%的把握认为空气质量的优良与汽车尾气的排放有关. ………12分