- 2021-06-10 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
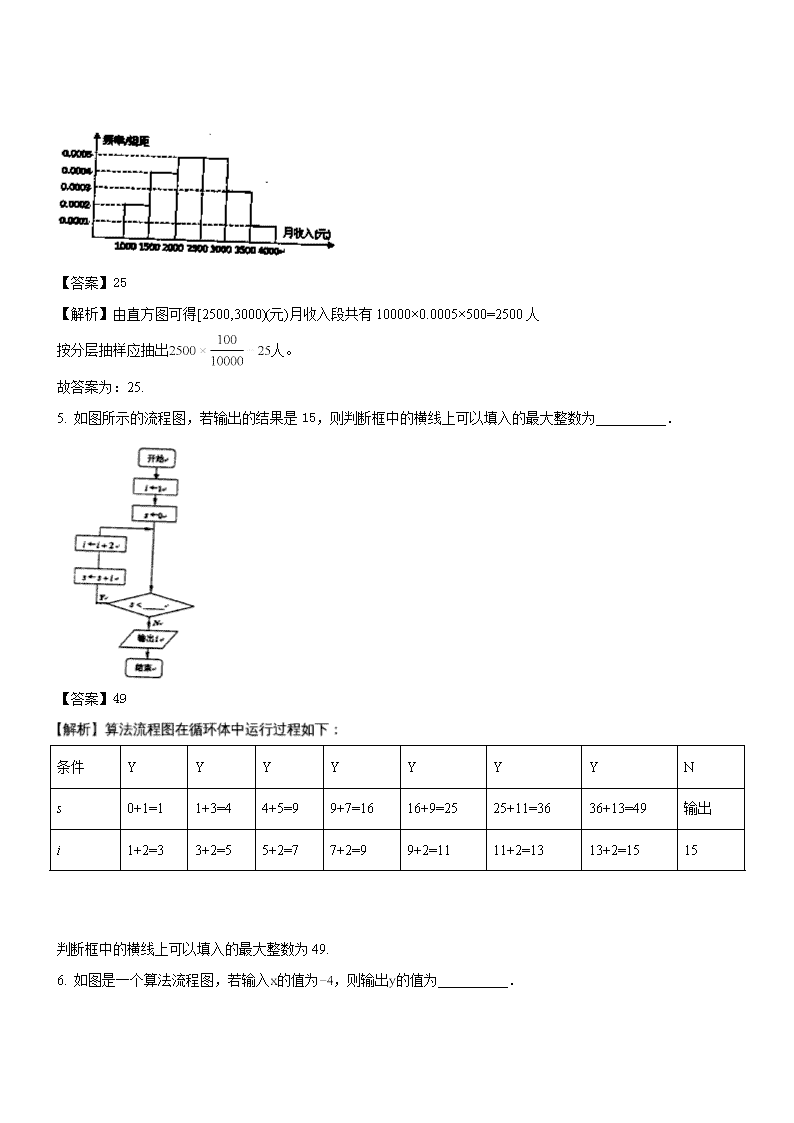
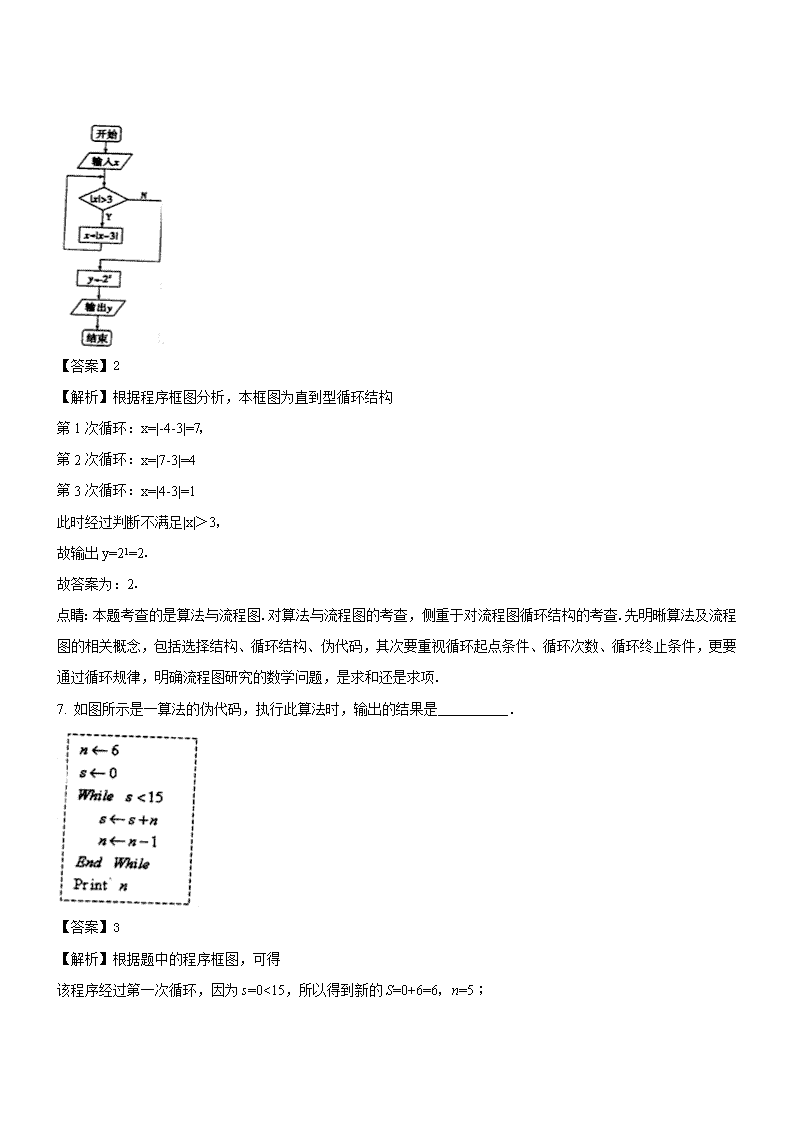
2017-2018学年江苏省泰州中学高二下学期4月月考数学理试题(解析版)
江苏省泰州中学2017-2018学年高二4月月考试题 数学(理) 一、填空题(将答案填在答题纸上) 1. 总体由编号为的50各个体组成,利用随机数表(以下摘取了随机数表中第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为__________. 66 67 40 67 14 64 05 71 95 86 11 05 65 09 68 76 83 20 37 90 57 16 00 11 66 14 90 84 45 11 75 73 88 05 90 52 27 41 14 86 【答案】09 【解析】从随机数表第1行的第9列和第10列数字开始, 依次是14,05,11,09, ∴第四个数字是09. 故答案为:09. 2. 已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8,则该组数据的方差为__________. 【答案】 【解析】 3. 已知为坐标原点,,若,则的坐标是__________. 【答案】 【解析】为坐标原点,,则. . 故答案为;. 4. 一个社会调查机构就某地居民的月收入调査了10000人,并根据所得数据画出了如图所示的频率分布直方图,现要从这10000人中再用分层抽样的方法抽出100人作进一步调査,则月收入在 (元)内应抽出__________人. 【答案】25 【解析】由直方图可得[2500,3000)(元)月收入段共有10000×0.0005×500=2500人 按分层抽样应抽出人。 故答案为:25. 5. 如图所示的流程图,若输出的结果是15,则判断框中的横线上可以填入的最大整数为__________. 【答案】49 条件 Y Y Y Y Y Y Y N s 0+1=1 1+3=4 4+5=9 9+7=16 16+9=25 25+11=36 36+13=49 输出 i 1+2=3 3+2=5 5+2=7 7+2=9 9+2=11 11+2=13 13+2=15 15 判断框中的横线上可以填入的最大整数为49. 6. 如图是一个算法流程图,若输入的值为,则输出的值为__________. 【答案】2 【解析】根据程序框图分析,本框图为直到型循环结构 第1次循环:x=|-4-3|=7, 第2次循环:x=|7-3|=4 第3次循环:x=|4-3|=1 此时经过判断不满足|x|>3, 故输出y=21=2. 故答案为:2. 点睛:本题考查的是算法与流程图.对算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 7. 如图所示是一算法的伪代码,执行此算法时,输出的结果是__________. 【答案】3 【解析】根据题中的程序框图,可得 该程序经过第一次循环,因为s=0<15,所以得到新的S=0+6=6,n=5; 然后经过第二次循环,因为s=6<15,所以得到新的S=6+5=11,n=4; 然后经过第三次循环,因为s=11<15,所以得到新的S=11+4=15,n=3; 接下来判断:因为s=15,不满足s<15,所以结束循环体并输出最后的n, 综上所述,可得最后输出的结果是3 故答案为:3 8. 已知实数,执行如图所示的流程图,则输出的不小于55的概率为__________. 【答案】 【解析】设实数x∈[1,9], 经过第一次循环得到x=2x+1,n=2, 经过第二循环得到x=2(2x+1)+1,n=3, 经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x, 输出的值为8x+7, 令8x+7⩾55,得x⩾6, 由几何概型得到输出的x不小于55的概率为. 故答案为:. 9. 若4名学生报名参加数学、计算机、航模兴趣小组,每人选报1项,则不同的报名方式有__________. 【答案】81 【解析】4名同学报名参加数学、计算机、航模兴趣小组,每人只选报1项,则每人有3种报名方法, 则4人共有3×3×3×3=81种方法, 故答案为:81. 10. 从0,1,2,3这四个数字中一次随机取两个数字,若用这两个数字组成无重复数字的两位数,则所得两位数为偶数的概率是__________. 【答案】 【解析】从0,1,2,3这四个数字中一次随机取两个数字组成无重复数字的两位数,分为两类:若取出的数字不含0,共组成个两位数,其中2为个位的两位数有个; 若取出的两个数字中有一个为0,则0只能放在个位上,可组成个两位数,且都是偶数. 由上可得所得两位数的个数为6+3=9个,其中偶数个数为2+3=5. 故所得两位数为偶数的概率P=. 故答案为. 11. 对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是__________.(答错任意一个均不给分) 【答案】46,45,56 【解析】有精液图可知,将数据从下到大排序,位于中间的两位数为:15和47,取其平均数可知中位数为46; 由于45出现了3次,出现的次数最多,因此其众数为45; 总体中最大值为68,最小值为12,所以极差为68-12=56. 故答案为:46,45,56. 12. 在不等式组所表示的平面区域内所有的格点(横、纵坐标均为整数的点称为格点)中任取3个点,则该3点恰能成为一个三角形的三个顶点的概率为__________. 【答案】 【解析】不等式组表示的平面区域内的格点有(2,1),(2,2),(3,1),(3,2),(3,3),共5个,从中任取3个点,有10种取法,其中共线的3点不能构成三角形,有(3,1),(3,2),(3,3)1种,即能够作为三角形3个顶点的情况有9种,故所求概率是. 13. 将参加夏令营的600名学生编号为001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第营区,从301到495在第营区,从496到600在第营区,三个营区被抽中的人数依次为__________. 【答案】25,17,8 【解析】依题意知,在随机抽样中,首次抽到003号,以后每隔12个号抽到一个人,则分别是003、015、027、039构成以3为首项,12为公差的等差数列,故可分别求出在001到300中有30012=25人,在301至495号中共有495−30112=17人,则496到600中有600−496−812=8人. 故答案为:25,17,8. 点睛:本题考查了抽样方法中的系统抽样问题,对于系统抽样的抽法是先对总体编号,根据样本平均分组,确定组距,再在第一组中抽取一个编号,依次等距抽取,其中把握系统抽样的原则是解答此类问题的关键. 14. 如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有__________种.(以数字作答) 【答案】72 【解析】由题意可知,当选用三种颜色着色,由乘法原理种方法,当选用四种颜色时,由乘法原理则种方法,再据加法原理可得种方法. 点睛:涂色问题一般是综合利用两个计数原理求解,但也有几种常用方法:按区域的不同,以区域为主分步计数,用分步乘法计数原理分析:以颜色为主分类讨论,适用于区域,点,线段等问题,用分类加法计数原理分析;将空间问题平面化,转化成平面区域的涂色问题. 第Ⅱ卷 二、解答题 (解答应写出文字说明、证明过程或演算步骤.) 15. 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是. (1)求图中的值; (2)根据频率分布直方图,估计这100名学生语文成绩的平均分; (3)若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数之比如下表所示,求数学成绩在之外的人数. 【答案】(1) (2)73(3)10 【解析】【试题分析】(1)依据题设利用频率之和为1建立方程分析求解;(2)依据题设中的频率分布直方图中提供的数据,运用加权平均数公式求解;(3)依据题设条件及频率分布表分析探求: (Ⅰ)由频率分布直方图,可得,因此 (Ⅱ),所以这100名学生的语文成绩的平均分为73分. 16. 某超市为了了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示. 已知这100位顾客中一次购物量超过8件的顾客占. (1)确定的值,并估计顾客一次购物的结算时间的平均值; (2)求一位顾客一次购物的结算时间不超过2.5分钟的概率.(将频率视为概率) 【答案】(1),平均值1.9 (2) 【解析】试题分析:(Ⅰ)由已知得25+y+10=55,x+30=45,故可确定,y的值,进而可求顾客一次购物的结算时间的平均值;(Ⅱ)记A:一位顾客一次购物的结算时间不超过2分钟;A1:该顾客一次购物的结算时间为1分钟;A2:该顾客一次购物的结算时间为1.5分钟;A3:该顾客一次购物的结算时间为2分钟;将频率视为概率求出相应的概率,利用互斥事件的概率公式即可得到结论 试题解析:(1)由已知得25+y+10=55,x+30=45,所以x=15,y=20. 该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,顾客一次购物的结算时间的平均值可用样本平均数估计,其估计值为 =1.9 (min). (2)记A为事件“一位顾客一次购物的结算时间不超过2 min”,A1,A2,A3分别表示事件“该顾客一次购物的结算时间为1 min”,“该顾客一次购物的结算时间为1.5 min”,“该顾客一次购物的结算时间为2 min”. 将频率视为概率得P(A1)==,P(A2)==,P(A3)==. 因为A=A1∪A2∪A3,且A1,A2,A3是互斥事件, 所以P(A)=P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=. 故一位顾客一次购物的结算时间不超过2 min的概率为. 考点:1.概率的应用;2.众数、中位数、平均数 17. 如图,在四棱锥中,底面是矩形,垂直于底面,,点为线段(不含端点)上一点. (1)当是线段的中点时,求与平面所成角的正弦值; (2)已知二面角的正弦值为,求的值. 【答案】(1) (2) 【解析】试题分析:(1)先根据题意建立空间直角坐标系,设立各点坐标,列方程组解出平面,再根据向量数量积求向量夹角,最后根据线面角与向量夹角互余关系求与平面所成角的正弦值;(2)列方程组解出平面,再根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系列等量关系,解方程可得的值.; 试题解析:(1)以为原点,,,为坐标轴,建立如图所示空间直角坐标系;设,则,,,,,; 所以,,, 设平面的法向量,则, 即,解得,所以平面的一个法向量, , 则与平面所成角的正弦值为. (2)由(1)知平面的一个法向量为,设,则, ,,设平面的法向量,则,即 ,解得,所以平面的一个法向量, 由题意得 , 所以,即, 因为,所以,则. 点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”. 18. 已知关于的一次函数. (1)设集合和,分别从集合和中随机取一个数作为和,求函数是增函数的概率; (2)实数满足条件,求函数的图象经过第一、二、三象限的概率. 【答案】(1) (2) 【解析】试题分析:(1)全部结果的基本事件有共个基本事件,设使函数为增函数的事件为有个基本事件,所以;(2)要使函数的图象过第一、二、三象限,则,故使函数图象过第一、二、三象限的的区域为第一象限的阴影部分,利用图形面积比即可求概率为. 试题解析:解:(1)抽取的全部结果的基本事件有: ,共个基本事件,设使函数为增函数的事件为,则包含的基本事件有:共个基本事件,所以. (2)满足条件的区域如图所示, 要使函数的图象过第一、二、三象限,则,故使函数图象过第一、二、三象限的的区域为第一象限的阴影部分,所以所求事件的概率为. 考点:1、古典概型;2、几何概型. 视频 19. 如图,圆锥的高,底面半径,为的中点,为母线的中点,为底面圆周上一点,满足. (1)求异面直线与所成角的余弦值; (2)求二面角的正弦值. 【答案】(1) (2) 【解析】(1)以O为原点,底面上过O点且垂直于OB的直线为x轴,OB所在的线为y轴,OP所在的线为z轴,建立空间直角坐标系,则 B(0,2,0),P(0,0,4),D(0,0,2),E(0,1,2). 设F(x0,y0,0)(x0>0,y0>0),且+=4, 则=(x0,y0-1,-2),=(0,1,0), ∵EF⊥DE,即⊥,则·=y0-1=0,故y0=1. ∴F(,1,0),=(,0,-2),=(0,-2,2). 设异面直线EF与BD所成角为α,则cosα=. (2)设平面ODF的法向量为n1=(x1,y1,z1),则 令x1=1,得y1=-,平面ODF的一个法向量为n1=(1,-,0). 设平面DEF的法向量为n2=(x2,y2,z2), 同理可得平面DEF的一个法向量为n2=. 设二面角ODFE的平面角为β,则|cosβ|==. ∴sinβ=. 20. 如图,在三棱柱中,平面,,且. (1)求棱与所成的角的大小; (2)在棱上确定一点,使二面角的平面角的余弦值为. 【答案】(1) (2) 【解析】试题分析:(1)因为AB⊥AC,A1B⊥平面ABC,所以以A为坐标原点,分别以AC、AB所在直线分别为x轴和y轴,以过A,且平行于BA1的直线为z轴建立空间直角坐标系,由AB=AC=A1B=2求出所要用到的点的坐标,求出棱AA1与BC上的两个向量,由向量的夹角求棱AA1与BC所成的角的大小; (2)设棱B1C1上的一点P,由向量共线得到P点的坐标,然后求出两个平面PAB与平面ABA1的一个法向量,把二面角P-AB-A1的平面角的余弦值为,转化为它们法向量所成角的余弦值,由此确定出P点的坐标. 试题解析: 解(1)如图,以为原点建立空间直角坐标系, 则, . , 故与棱所成的角是. (2)为棱中点, 设,则. 设平面的法向量为,, 则, 故 而平面的法向量是,则, 解得,即为棱中点,其坐标为. 点睛:本题主要考查线面垂直的判定与性质,以及利用空间向量求二面角.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.查看更多