2018-2019学年湖北省黄冈市高二下学期期末考试数学文试题（Word版）

2018-2019学年湖北省黄冈市高二下学期期末考试数学文试题（Word版）

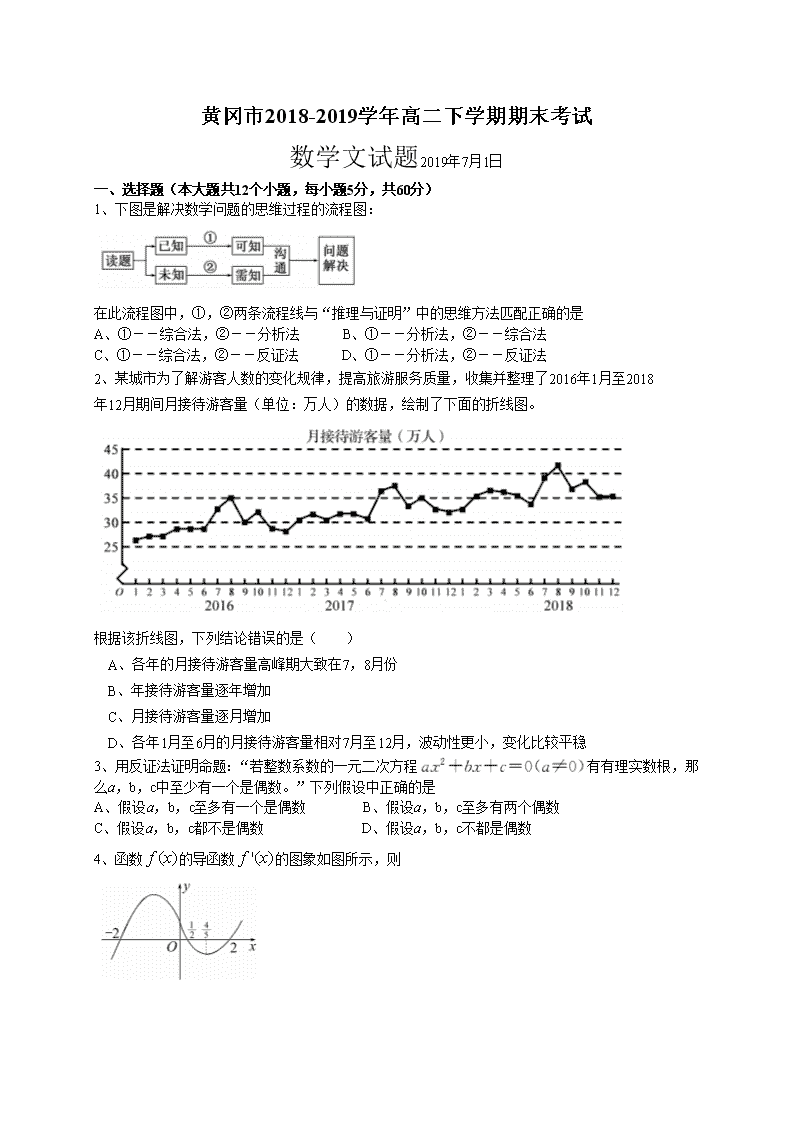
黄冈市2018-2019学年高二下学期期末考试 数学文试题2019年7月1日 一、选择题（本大题共12个小题，每小题5分，共60分）‎ ‎1、下图是解决数学问题的思维过程的流程图：‎ 在此流程图中，①，②两条流程线与“推理与证明”中的思维方法匹配正确的是 A、①－－综合法，②－－分析法　　　B、①－－分析法，②－－综合法 C、①－－综合法，②－－反证法　　　D、①－－分析法，②－－反证法 ‎2、某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2016年1月至2018‎ 年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图。‎ 根据该折线图，下列结论错误的是（　　）‎ A、各年的月接待游客量高峰期大致在7，8月份 B、年接待游客量逐年增加 C、月接待游客量逐月增加 D、各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 ‎3、用反证法证明命题：“若整数系数的一元二次方程有有理实数根，那 么a，b，c中至少有一个是偶数。”下列假设中正确的是 A、假设a，b，c至多有一个是偶数　　　　B、假设a，b，c至多有两个偶数 C、假设a，b，c都不是偶数　　　　　　　D、假设a，b，c不都是偶数 ‎4、函数的导函数的图象如图所示，则 A、为的极大值点　　　B、－2为的极大值点 C、2为的极大值点　　　D、为的极小值点 ‎5、函数的图象可能为 ‎6、是“复数是纯虚数”的 A、充分而不必要条件　　B、必要而不充分条件 C、充分必要条件　　　　D、既不充分也不必要条件 ‎7、若函数的值域是［0，3］，则函数F（x）＝2－f（x－3），的值域是 ‎　A、［0，3］　　　　B、［1，4］　　　　C、［－1，2］　　　D、［2，5］‎ ‎8、已知二次函数的二次项系数为a，且不等式的解集为（1,3），若方程 ‎，有两个相等的根，则实数a＝‎ ‎　　A、－　　　　B、1　　　　　C、1或－　　　　D、－1或－‎ ‎9、下列命题中正确的个数 ‎①的否定是 ‎②用相关指数R2可以刻画回归的拟合效果，R2值越小说明模型的拟合效果越好；‎ ‎③命题“若a＞b＞0，则)”的逆命题为真命题；‎ ‎④若的解集为R，则m≥1‎ A、0 　　　B、1 　　C、2 　　D、3‎ ‎10、设函数，集合A＝｛x｜y＝f（x）｝，B＝｛y｜y＝f（x）｝，则图中的阴影部分表示的集合为（　　）‎ ‎　‎ ‎11、已知不等于 ‎12、设是定义在R上的可导偶函数，且f（2）＝2，若当x＜0时，，‎ 则函数的零点个数为 ‎　A、0　　　　B、1　　　　C、2　　　　D、0或2‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13、下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产品x（吨）与相应的生产能耗y(吨)的几组对应数据，根据表中提供的数据，求出y关于x 的线性回归方程为，那么表中t的值为＿＿＿‎ ‎14、若，则x＋y＝＿＿＿‎ ‎15、已知定义在R上的奇函数f（x）满足f（x＋1）＝f（1－x），当0≤x≤1，，则＝＿＿＿＿‎ ‎16、已知数集，且有下列说法 ‎，则满足的数值有＿＿＿组 三、解答题（本大题共6个小题，满分70分。解答应写出文字说明0证明过程或演算步骤）‎ ‎17、（本小题满分12分）‎ 已知复数是纯虚数，i是虚数单位。‎ ‎（1）求复数z的共轭复数；‎ ‎（2）若复数所表示的点在第二象限，求实数m的取值范围。‎ ‎18、（本小题满分12分）‎ 设函数，曲线在点处的切线方程为。‎ ‎（1）求的解析式；‎ ‎（2）证明：曲线上任一点处的切线与直线x=0和直线y＝x所围成的三角形的面 积为定值，并求此定值。‎ ‎19、（本小题满分12分）‎ 已知是定义在R上的奇函数，当x≥0时，‎ ‎（1）求函数的解析式；‎ ‎（2）若－1＜＜1，求实数的取值范围。‎ ‎20、（本小题满分12分）‎ 中国是世界互联网服务应用最好的国家，一部智能手机就可以跑遍国内所有地方，中国市场的移动支付普及率高得惊人.一家大型超市委托某高中数学兴趣小组调查该超市的顾客使用移动支付的情况。调查人员从年龄在［20，60）内的顾客中，随机抽取了200人，调查他们是否使用移动支付，结果如下表：‎ ‎（I）为更进一步推动移动支付，超市准备对使用移动支付的每位顾客赠送1个环保购物 袋。若某日该超市预计有10000人购物，试根据上述数据估计，该超市当天应准备多少 个环保购物袋？‎ ‎（II）填写下面列联表，并根据列联表判断是否有99.9%的把握认为使用移动支付与年龄 有关？‎ 附：下面的临界值表供参考：‎ ‎21、（本小题满分12分）‎ 设函数 ‎（1）判断函数: 在［1，＋∞）的单调性；‎ ‎（2）对于区间［1.2］上的任意不相等实数x1，x2，都有成立，求实数a的取值范围!‎ 请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分，解答时请写清 题号。‎ ‎22、（选修4－4：极坐标系与参数方程）‎ 在直角坐标系xoy中，直线l的参数方程为（t为参数），以坐标原点为极点，‎ x轴正半轴为极轴建立极坐标系，圆C极坐标方程为。‎ ‎（1）求直线l的普通方程和圆C的直角坐标方程；‎ ‎（2）若直线l与圆C相切，求m的值。‎ ‎23．（选修4-5：不等式选讲）‎ 已知函数 ‎（1）解不等式；‎ ‎（2）当［1，2］时，恒成立，求实数a的取值范围。‎ 黄冈市2019春季高二数学期末测试题（文科）‎ 一、选择题 A CCA C BCACC DC ‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．4 14．2 15．-1 16．3‎ ‎ 三、解答题（共70分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．解:（1）∵z＝bi（b∈R），∴．‎ 又∵是纯虚数，∴，∴，即．………………………………………5分 所以 ………………………………………6分 ‎（2）∵，∈，∴，……8分 又∵复数所表示的点在第二象限，∴解得， ‎ 即时，复数所表示的点在第二象限． ………………………………12分 ‎18．(1)解　方程3x－2y－4＝0可化为，当x＝2时，．又f′(x)＝a＋，‎ 于是　解得，故．………………………………5分 ‎(2)证明　设P(x0，y0)为曲线上任一点，由y′＝1＋，知曲线在点P(x0，y0)处的切线方程为 y－y0＝(x－x0)，即y－＝(x－x0)．………………………………7分 令x＝0，得y＝－，从而得切线与直线x＝0的交点坐标为．‎ 令y＝x，得y＝x＝2x0，从而得切线与直线y＝x的交点坐标为(2x0,2x0)．‎ 所以点P(x0，y0)处的切线与直线x＝0，y＝x所围成的三角形的面积为S＝|2x0|＝4．‎ 故曲线y＝f(x)上任一点处的切线与直线x＝0，y＝x所围成的三角形的面积为定值且此定值为4．‎ ‎ ………………………………12分 ‎ ‎ ‎19．解：(1)当x<0时，－x>0，由题意知f(－x)＝loga(－x＋1)．‎ 又f(x)是定义在R上的奇函数，所以f(－x)＝－f(x)．所以当x<0时，－f(x)＝loga(－x＋1)，‎ 所以函数f(x)的解析式为f(x)＝………………………………6分 ‎(2)因为－11时，原不等式等价于解得a>3； ………………………………9分 ‎②当0 0时，f (x1) < f (x2)，g (x1) < g (x2) ‎ ‎∴可化为 ∴ 设，即 ∵F (x)在[1，2]上单调递减，∴恒成立 即在[1，2]上恒成立 ∵，∴0 < a≤1．…………………………12分 ‎（二）选考题：共10分．请考生在22、23题中选择一题作答．如果多做，则按所做题的第一题计分．‎ ‎22．（选修4-4：极坐标系与参数方程）‎ 解：（1）由题意得，直线的普通方程为，‎ 圆的直角坐标方程为． …………………………5分 ‎（2）因为直线与圆相切，所以，解得；‎ ‎ 所以的值为． …………………………10分 ‎23．（选修4-5：不等式选讲）‎ 解：（1）原不等式等价于 或或 解得，所以不等式的解集为 …………………………5分 ‎（2）当时，，不等式可以化为，‎ 因为，，所以，‎ 所以。 …………………………10分