- 2021-06-10 发布 |
- 37.5 KB |
- 133页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
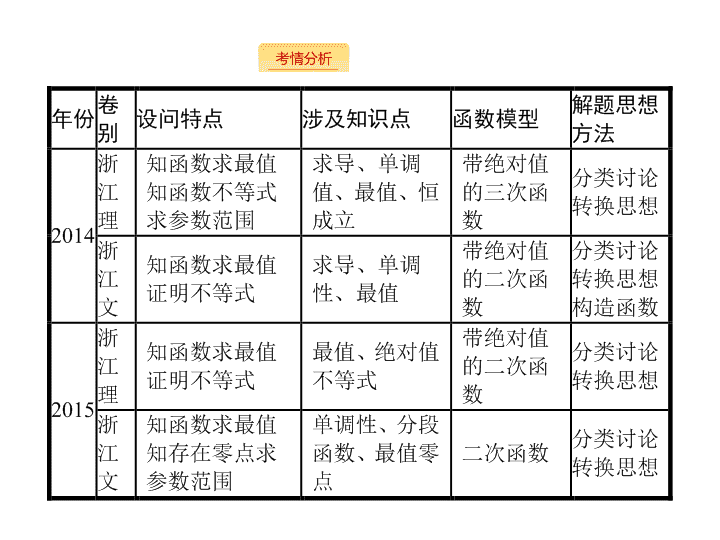
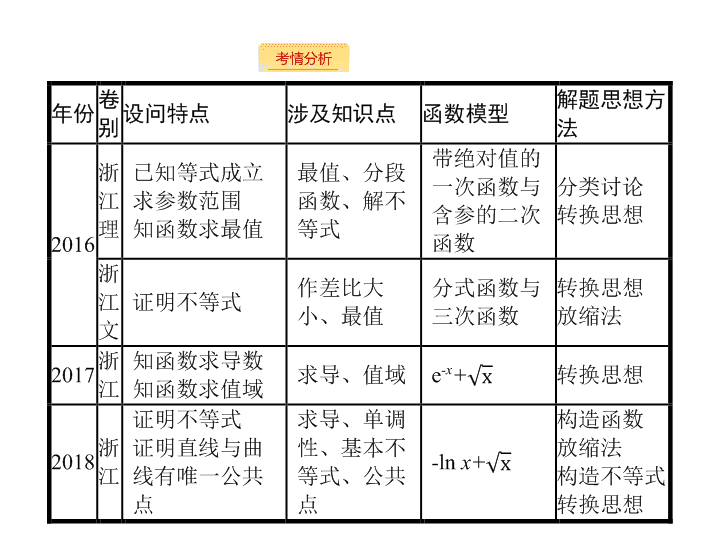
2019届二轮复习函数、导数、方程、不等式课件(133张)(全国通用)
6.4 函数、导数、方程、不等式 - 2 - - 3 - - 4 - 1 . 导数的几何意义 (1) 函数 f ( x ) 在 x 0 处的导数是曲线 f ( x ) 在点 P ( x 0 , f ( x 0 )) 处的切线的斜率 , 即 k=f' ( x 0 ) . (2) 函数切线问题的求解策略 : 用好切点 “ 三重性 ”: ① 切点在函数图象上 , 满足函数解析式 ; ② 切点在切线上 , 满足切线方程 ; ③ 切点处的导数等于切线的斜率 . 2 . 函数的导数与单调性的关系 函数 y=f ( x ) 在 ( a , b ) 内可导 , (1) 若 f' ( x ) > 0 在 ( a , b ) 内恒成立 , 则 f ( x ) 在 ( a , b ) 内单调递增 ; (2) 若 f' ( x ) < 0 在 ( a , b ) 内恒成立 , 则 f ( x ) 在 ( a , b ) 内单调递减 . 3 . 函数的导数与单调性的等价关系 函数 f ( x ) 在 ( a , b ) 内可导 , f' ( x ) 在 ( a , b ) 任意子区间内都不恒等于 0 .f' ( x ) ≥ 0 ⇔ f ( x ) 在 ( a , b ) 上为增函数 .f' ( x ) ≤ 0 ⇔ f ( x ) 在 ( a , b ) 上为减函数 . - 5 - 4 . 函数的极值、最值 (1) 若在 x 0 附近左侧 f' ( x ) > 0, 右侧 f' ( x ) < 0, 则 f ( x 0 ) 为函数 f ( x ) 的极大值 ; 若在 x 0 附近左侧 f' ( x ) < 0, 右侧 f' ( x ) > 0, 则 f ( x 0 ) 为函数 f ( x ) 的极小值 . (2) 设函数 y=f ( x ) 在 [ a , b ] 上连续 , 在 ( a , b ) 内可导 , 则 f ( x ) 在 [ a , b ] 上必有最大值和最小值且在极值点或端点处取得 . (3) 若函数 f ( x ) 在 [ a , b ] 上单调递增 , 则 f ( a ) 为函数的最小值 , f ( b ) 为函数的最大值 ; 若函数 f ( x ) 在 [ a , b ] 上单调递减 , 则 f ( a ) 为函数的最大值 , f ( b ) 为函数的最小值 . 5 . 常见恒成立不等式 (1)ln x ≤ x- 1;(2)e x ≥ x+ 1 . - 6 - 6 . 构造辅助函数的四种方法 (1) 移项法 : 证明不等式 f ( x ) >g ( x )( f ( x )查看更多