2019届二轮复习小题综合限时练（三）作业（全国通用）

2019届二轮复习小题综合限时练（三）作业（全国通用）

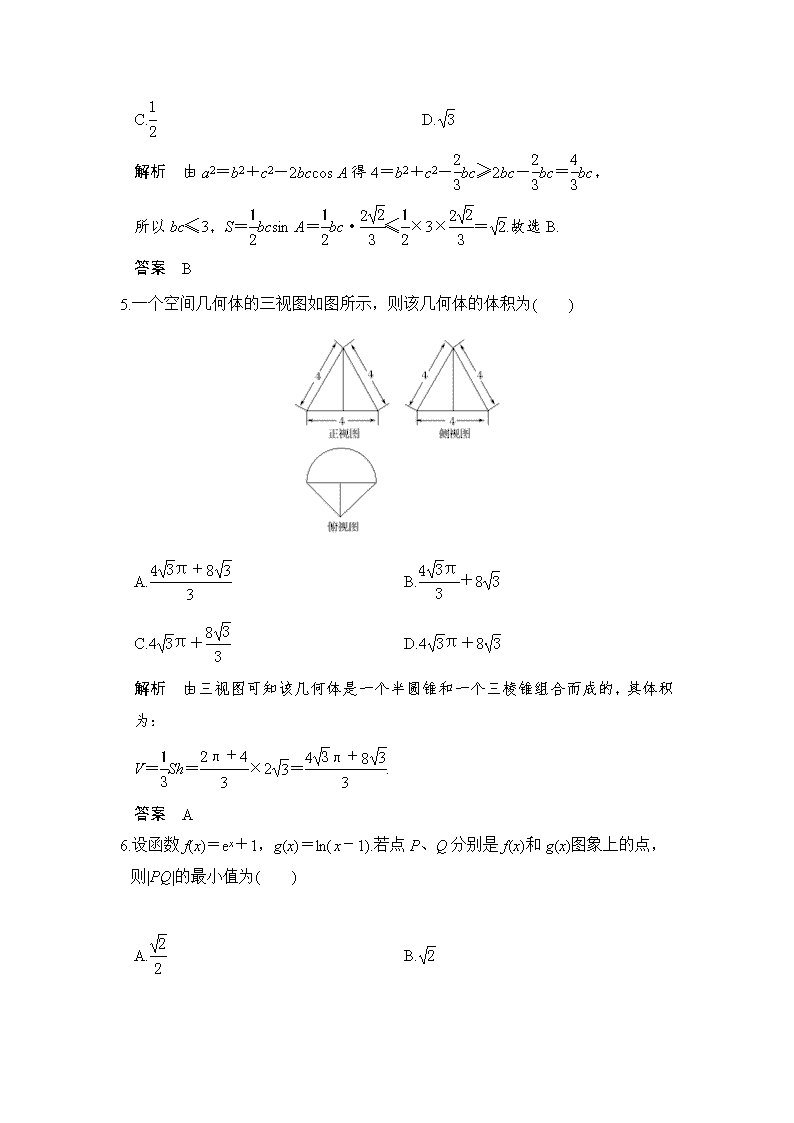
‎ (限时：40分钟)‎ 一、选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.)‎ ‎1.设i是虚数单位，若复数z与复数z0＝1－2i在复平面上对应的点关于实轴对称，则z0·z＝(　　)‎ A.5 B.－3 ‎ C.1＋4i D.1－4i 解析　因为z0＝1－2i，所以z＝1＋2i，故z0·z＝5.故选A.‎ 答案　A ‎2.已知直线y＝x与双曲线C：－＝1(a＞0，b＞0)有两个不同的交点，则双曲线C的离心率的取值范围是(　　)‎ A.(1，) B.(1，2)‎ C.(，＋∞) D.(2，＋∞)‎ 解析　直线y＝x与C有两个不同的公共点⇒＞⇒e＞2.故选D.‎ 答案　D ‎3.设函数y＝f(x)的图象与y＝2x＋a的图象关于直线y＝－x对称，且f(－2)＋‎ f(－4)＝1，则a等于(　　)‎ A.－1 B.1‎ C.2 D.4‎ 解析　设f(x)上任意一点为(x，y)关于y＝－x的对称点为(－y，－x)，将(－y，－x)代入y＝2x＋a，所以y＝a－log2(－x)，由f(－2)＋f(－4)＝1，得a－1＋a－2＝1，2a＝4，a＝2.‎ 答案　C ‎4.已知△ABC的三个内角A、B、C所对的边分别为a、b、c.若a＝2，cos A＝，则△ABC面积的最大值为(　　)‎ A.2 B. ‎ C. D. 解析　由a2＝b2＋c2－2bccos A得4＝b2＋c2－bc≥2bc－bc＝bc，‎ 所以bc≤3，S＝bcsin A＝bc·≤×3×＝.故选B.‎ 答案　B ‎5.一个空间几何体的三视图如图所示，则该几何体的体积为(　　)‎ A. B.＋8 C.4π＋ D.4π＋8 解析　由三视图可知该几何体是一个半圆锥和一个三棱锥组合而成的，其体积为：‎ V＝Sh＝×2＝.‎ 答案　A ‎6.设函数f(x)＝ex＋1，g(x)＝ln(x－1).若点P、Q分别是f(x)和g(x)图象上的点，则|PQ|的最小值为(　　)‎ A. B. ‎ C. D.2 解析　f(x)＝ex＋1与g(x)＝ln(x－1)的图象关于直线y＝x对称，平移直线y＝x使其分别与这两个函数的图象相切.由f′(x)＝ex＝1得，x＝0.切点坐标为(0，2)，‎ 其到直线y＝x的距离为，故|PQ|的最小值为2.故选D.‎ 答案　D ‎7.已知F为双曲线－＝1(a＞0，b＞0)的左焦点，点A为双曲线虚轴的一个顶点，过F，A的直线与双曲线的一条渐近线在y轴右侧的交点为B，若＝(－1)，则此双曲线的离心率是(　　)‎ A. B. ‎ C.2 D. ‎ 解析　过F，A的直线方程为y＝(x＋c)①，一条渐近线方程为y＝x②，联立①②，‎ 解得交点B，‎ 由＝(－1)，得c＝(－1)，c＝a，e＝.‎ 答案　A ‎8.已知函数f(x)＝若f(f(m))≥0，则实数m的取值范围是(　　)‎ A.[－2，2] B.[－2，2]∪[4，＋∞)‎ C.[－2，2＋] D.[－2，2＋]∪[4，＋∞)‎ 解析　令f(m)＝n，则f(f(m))≥0就是f(n)≥0.画出函数f(x)的图象可知，－1≤n≤1，或n≥3，即－1≤f(m)≤1或f(m)≥3.‎ 由1－|x|＝－1得x＝－2.‎ 由x2－4x＋3＝1，x＝2＋，x＝2－(舍).‎ 由x2－4x＋3＝3得，x＝4.‎ 再根据图象得到，m∈[－2，2＋]∪[4，＋∞).故选D.‎ 答案　D 二、填空题(本大题共7小题，多空题每题6分，单空题每题4分，共36分.)‎ ‎9.已知x展开式中的常数项为20，其中a＞0，则a＝________.‎ 解析　Tr＋1＝Cx·x5－r·＝arCx6－r.‎ 由得因为a＞0，所以a＝.‎ 答案　 ‎10.已知双曲线－＝1的左、右焦点分别为F1，F2，P是双曲线右支上一点，则|PF1|－|PF2|＝________；离心率e＝________.‎ 解析　依题意，|PF1|－|PF2|＝2a＝2，离心率e＝＝＝.‎ 答案　2　 ‎11.已知函数f(x)＝则f(f(2))＝________，值域为________.‎ 解析　依题意，f(2)＝f(1)＝2，f[f(2)]＝f(2)＝2；因为f(x)＝f(x－1)，所以函数f(x)具有周期性，故函数f(x)的值域为(－1，2].‎ 答案　2　(－1，2]‎ ‎12.将函数y＝sin 2x的图象向右平移φ个单位长度后所得图象的解析式为y＝sin，则φ＝________，再将函数y＝sin图象上各点的横坐标伸长到原来的2倍(纵坐标不变)后得到的图象的解析式为________.‎ 解析　依题意，sin＝sin，故φ＝.将y＝sin图象上各点的横坐标伸长到原来的2倍后得到y＝sin的图象.‎ 答案　　y＝sin ‎13.已知是等差数列，f(1)＝2，f(2)＝6，则f(n)＝________，数列{an}满足an＋1＝f(an)，a1＝1，数列的前n项和为Sn，则S2015＋＝________.‎ 解析　由题意可得＝2，＝3，又是等差数列，则公差为1，所以＝2＋(n－1)＝n＋1，f(n)＝n(n＋1)＝n2＋n；an＋1＝f(an)＝an(an＋1)，则＝＝－，所以＝－，S2015＝＋＋…＋＝＋＋…＋＝－，所以S2015＋＝＝1.‎ 答案　n2＋n　1‎ ‎14.设a、b是单位向量，其夹角为θ.若|ta＋b|的最小值为，其中t∈R，则θ＝________.‎ 解析　因为t∈R，所以|ta＋b|2＝t2＋2tcos θ＋1＝(t＋cos θ)2＋1－cos2θ≥1－cos2θ＝.得cos θ＝±⇒θ＝或.‎ 答案　或 ‎15.已知数列{an}的各项取倒数后按原来顺序构成等差数列，各项都是正数的数列{xn}满足x1＝3，x1＋x2＋x3＝39，xann＝xan＋1n＋1＝xan＋2n＋2，则xn＝________.‎ 解析　设xann＝xan＋1n＋1＝xan＋2n＋2＝k，则an＝logxnk⇒＝logkxn，同理＝logkxn＋1，＝logkxn＋2，因为数列{an}的各项取倒数后按原来顺序构成等差数列，所以2logkxn＋1＝logkxn＋logkxn＋2⇒x＝xnxn＋2，所以数列{xn}是等比数列，把x1＝3代入x1＋x2＋x3＝39得公比q＝3(负值舍去)，所以xn＝3×3n－1＝3n.‎ 答案　3n