- 2021-06-09 发布 |
- 37.5 KB |
- 15页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014高一数学(人教A版)必修2能力强化提升:第一章综合素能检测
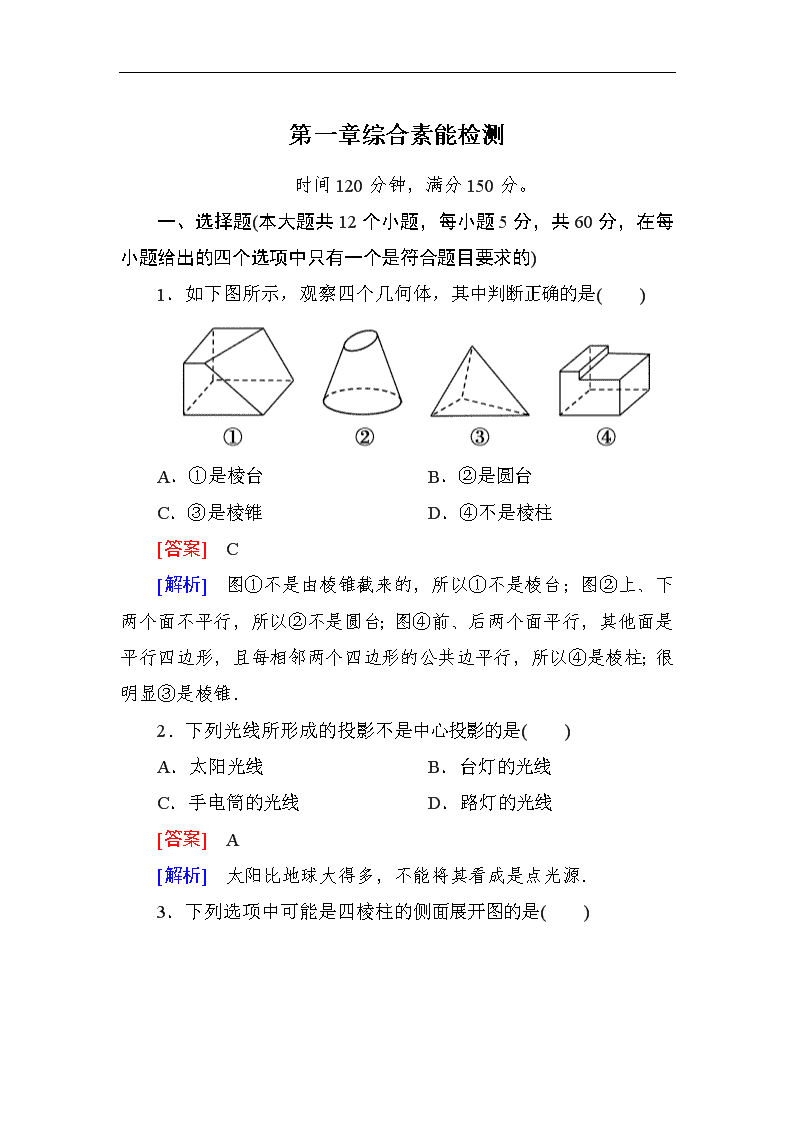
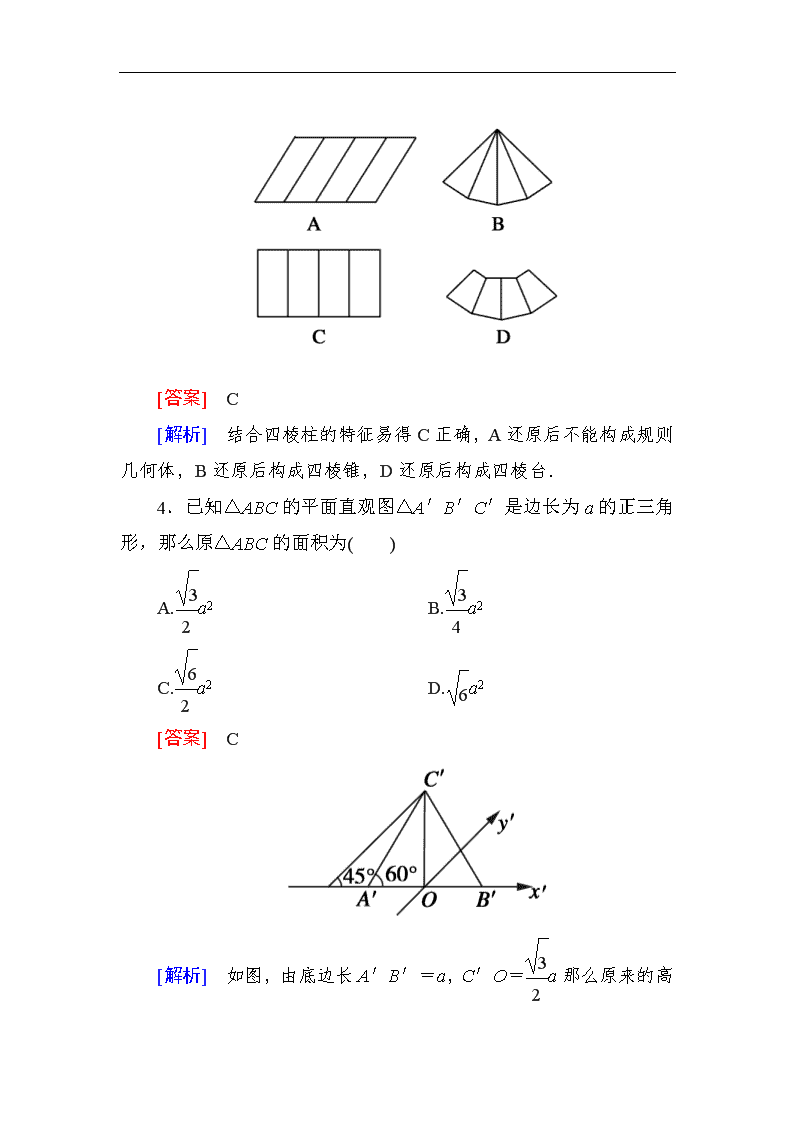
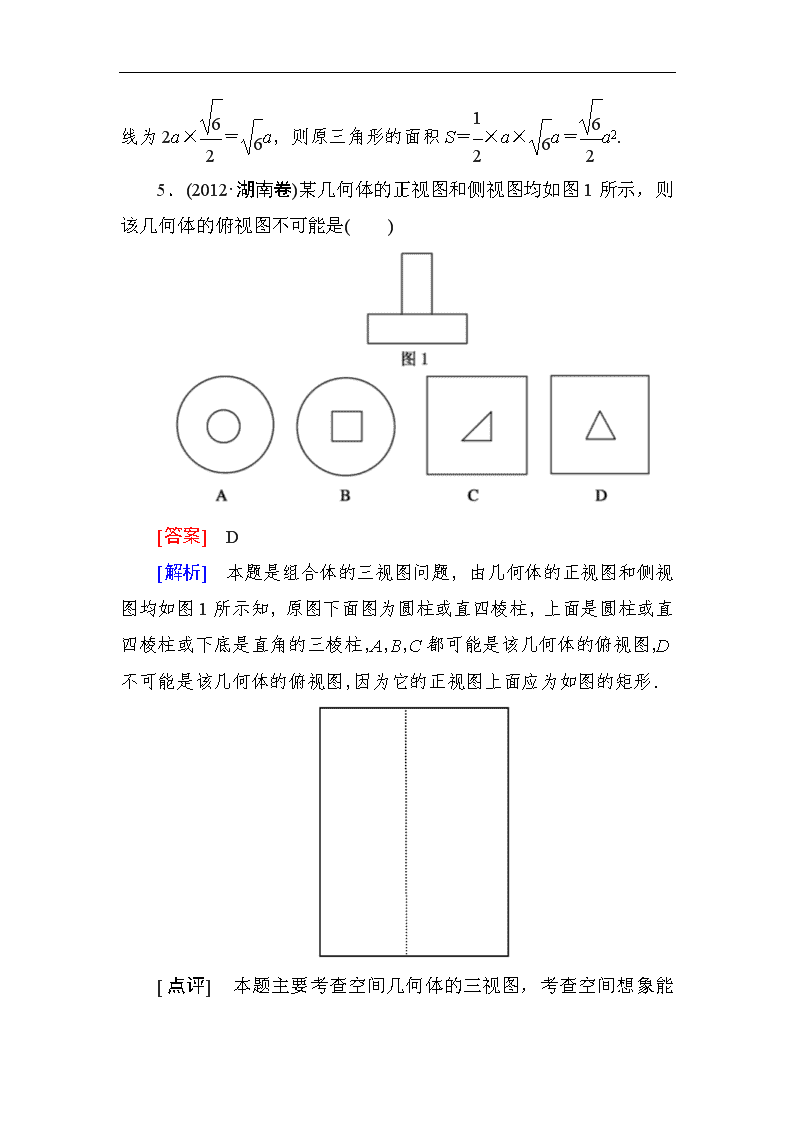
第一章综合素能检测 时间120分钟,满分150分。 一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的) 1.如下图所示,观察四个几何体,其中判断正确的是( ) A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱 [答案] C [解析] 图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱;很明显③是棱锥. 2.下列光线所形成的投影不是中心投影的是( ) A.太阳光线 B.台灯的光线 C.手电筒的光线 D.路灯的光线 [答案] A [解析] 太阳比地球大得多,不能将其看成是点光源. 3.下列选项中可能是四棱柱的侧面展开图的是( ) [答案] C [解析] 结合四棱柱的特征易得C正确,A还原后不能构成规则几何体,B还原后构成四棱锥,D还原后构成四棱台. 4.已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,那么原△ABC的面积为( ) A.a2 B.a2 C.a2 D.a2 [答案] C [解析] 如图,由底边长A′B′=a,C′O=a那么原来的高线为2a×=a,则原三角形的面积S=×a×a=a2. 5.(2012·湖南卷)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( ) [答案] D [解析] 本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形. [点评] 本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型. 6.(2012-2013山东省郯城一中高一第二次月考试题)正方体内切球与外接球体积之比为( ) A.1: B.1:3 C.1:3 D.1:9 [答案] C [解析] 设正方体棱长为a,内切球半径R1,外接球半径R2. R1=,R2=a, V内:V外=()3:(a)3=1:3. 故选C. 7.(2012~2013·浙江龙岩一模)有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( ) A.12π cm2 B.15π cm2 C.24π cm2 D.36π cm2 [答案] C [解析] 由三视图可知该几何体是圆锥,S表=S侧+S底=πrl+πr2=π×3×5+π×32=24π(cm2),故选C. 8.圆锥的高扩大到原来的2倍,底面半径缩短到原来的,则圆锥的体积( ) A.缩小到原来的一半 B.扩大到原来的2倍 C.不变 D.缩小到原来的 [答案] A [解析] V=π2×2h=πr2h,故选A. 9.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( ) A.7 B.6 C.5 D.3 [答案] A [解析] 设圆台较小底面圆的半径为r,由题意,另一底面圆的半径R=3r. ∴S侧=π(r+R)l=π(r+3r)×3=84π,解得r=7. 10.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( ) A.,1 B.,1 C., D., [答案] C [解析] 设球的半径为R, 则圆柱的底面半径为R,高为2R, ∴V圆柱=πR2×2R=2πR3,V球=πR3. ∴==, S圆柱=2πR×2R+2×πR2=6πR2,S球=4πR2. ∴==. 11.(2012-2013·广东惠州一模)某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( ) A.24 B.80 C.64 D.240 [答案] B [解析] 该几何体的四棱锥,高等于5,底面是长、宽分别为8、6的矩形,则底面积S=6×8=48,则该几何体的体积V=Sh=×48×5=80. 12.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是( ) [答案] B [解析] 画出该几何体的正视图为,其上层有两个立方体,下层中间有三个立方体,两侧各一个立方体,故B项满足条件. 二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.在几何体①圆锥;②正方体;③圆柱;④球;⑤正四面体中,三视图完全一样的是________. [答案] ②④ 14.用斜二测画法画边长为2的正三角形的直观图时,如果在已知图形中取的x轴和正三角形的一边平行,则这个正三角形的直观图的面积是________. [答案] /2 15.圆台的底半径为1和2,母线长为3,则此圆台的体积为________. [答案] π [解析] 圆台高h==2, ∴体积V=(r2+R2+Rr)h=π. 16.(2012-2013·安徽皖南八校联考)一个几何体的三视图及其尺寸如下图所示,其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是________. [答案] 2(1+)π+4 [解析] 此几何体是半个圆锥,直观图如图所示,先求出圆锥的侧面积S圆锥侧=πrl=π×2×2=4π,S底=π×22=4π, S△SAB=×4×2=4, 所以S表=++4 =2(1+)π+4. 三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)画出如图所示几何体的三视图. [解析] 该几何体的上面是一个圆柱,下面是一个四棱柱,其三视图如图所示. 18.(本题满分12分)一个圆台的母线长为12 cm,两底面面积分别为4πcm2和25π cm2.求: (1)圆台的体积; (2)截得此圆台的圆锥的母线长. [解析] (1)圆台的轴截面是等腰梯形ABCD(如图).由已知可得上底半径O1A=2 cm,下底半径OB=5 cm.又∵腰长为12 cm,∴高AM==3(cm),∴所求体积为×(4π++25π)×3=39π cm3. (2)设截得此圆台的圆锥的母线长为l, 则由△SAO1∽△SBO可得=, ∴l=20(cm). 即截得此圆台的圆锥的母线长为20 cm. 19.(本题满分12分)如下图所示是一个空间几何体的三视图,试用斜二测画法画出它的直观图(尺寸不限). [解析] 由三视图可知该几何体是一个正三棱台. 画法:(1)如图①所示,作出两个同心的正三角形,并在一个水平放置的平面内画出它们的直观图; (2)建立z′轴,把里面的正三角形向上平移高的大小; (3)连接两正三角形相应顶点,并擦去辅助线,被遮的线段用虚线表示,如图②所示,即得到要画的正三棱台. 20.(本题满分12分)如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2 m,高为 m,制造这个塔顶需要多少铁板? [解析]如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP. 在Rt△SOP中,SO=(m),OP=BC=1(m), 所以SP=2(m), 则△SAB的面积是×2×2=2(m2). 所以四棱锥的侧面积是4×2=8(m2), 即制造这个塔顶需要8m2铁板. 21.(本题满分12分)如图是一个几何体的正视图和俯视图. (1)试判断该几何体是什么几何体? (2)画出其侧视图,并求该平面图形的面积; (3)求出该几何体的体积. [解析] (1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥. (2)该几何体的侧视图如图.其中AB=AC,AD⊥BC,且BC的长是俯视图正六边形对边的距离,即BC=a,AD是正六棱锥的高,即AD=a,所以该平面图形的面积为·a·a=a2. (3)设这个正六棱锥的底面积是S,体积为V, 则S=6×a2=a2, 所以V=×a2×a=a3. 22.(本题满分12分)某高速公路收费站入口处的安全标识墩如图(1)所示.墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.如图(2)(3)所示的分别是该标识墩的正(主)视图和俯视图. (1)请画出该安全标识墩的侧(左)视图; (2)求该安全标识墩的体积. [解析] (1)如图所示. (2)该安全标识墩的体积V=VP-EFGH+VABCD-EFGH=×402×60+402×20=32 000+32 000 =64 000(cm3).查看更多