- 2021-06-09 发布 |
- 37.5 KB |
- 65页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习统计学案(全国通用)
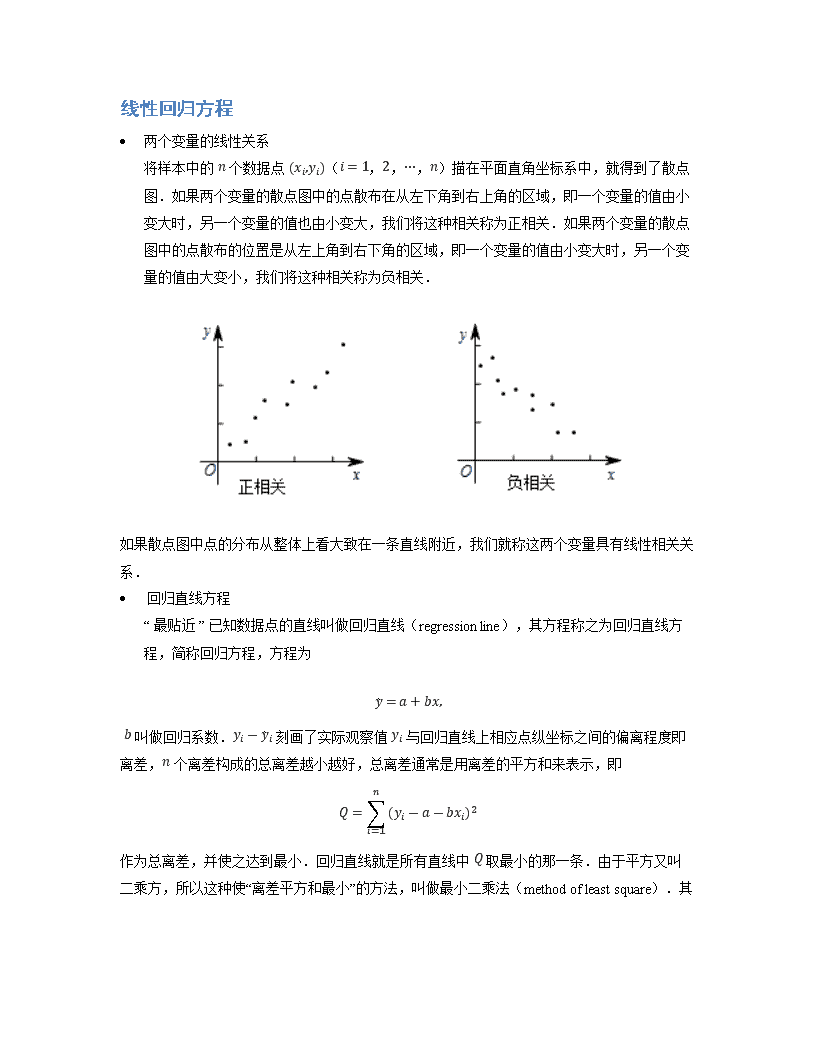
用样本估计总体 用样本的频率分布估计总体的分布,可以用样本的数字特征(如平均数、标准差)估计总体的 数字特征. 茎叶图 茎叶图(stem-and-leaf display)是统计学中用来表示数据的一种图.茎是指中间的一列数,叶 就是从茎的旁边生长出来的数.茎叶图不仅能够保留原始数据,而且能够显示数据的分布情况. 样本数据的数字特征 众数、中位数 一组数据中出现次数最多的数据称为这组数据的众数(mode). 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于 中间位置的数为这组数据的中位数(median);如果数据个数是偶数,则称中间两个数据 的平均数为这组数据的中位数. 标准差、方差 考察样本数据的分散程度的大小,最常用的统计量是标准差(standard deviation).标准差 是样本数据到平均数的一种平均距离,一般用 ��� 表示. 假设样本数据是 ��� , �� , � , �� , ��� 表示这组数据的平均数. ��� 到 ��� 的距离是 ��� � �� ( � ‴ � , � , � , � ).于是,样本数据 ��� , �� , � , ��� 到 ��� 的“平均距离”是 � ‴ ���������������������� � .由于上式含有绝对值,运算起来不太方便,因此,通常改用如下公 式来计算标准差 � ‴ � � �� � � � � �� � � � � � � �� � � � . 方差(variance)是标准差的平方 � � . � � ‴ � � �� � � � � �� � � � � � � �� � � � . 变量间的相关关系 变量与变量之间的关系常见的有两类:一类是确定性的函数关系;另一类是变量间确实存在关 系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的. 线性回归方程 两个变量的线性关系 将样本中的 � 个数据点 ����� ( � ‴ � , � , � , � )描在平面直角坐标系中,就得到了散点 图.如果两个变量的散点图中的点散布在从左下角到右上角的区域,即一个变量的值由小 变大时,另一个变量的值也由小变大,我们将这种相关称为正相关.如果两个变量的散点 图中的点散布的位置是从左上角到右下角的区域,即一个变量的值由小变大时,另一个变 量的值由大变小,我们将这种相关称为负相关. 如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量具有线性相关关 系. 回归直线方程 “ 最贴近 ” 已知数据点的直线叫做回归直线(regression line),其方程称之为回归直线方 程,简称回归方程,方程为 �� ‴ h � l�� l 叫做回归系数. �� � �� � 刻画了实际观察值 �� 与回归直线上相应点纵坐标之间的偏离程度即 离差, � 个离差构成的总离差越小越好,总离差通常是用离差的平方和来表示,即 � ‴ �‴� � �� � h � l�� � � 作为总离差,并使之达到最小.回归直线就是所有直线中 � 取最小的那一条.由于平方又叫 二乘方,所以这种使“离差平方和最小”的方法,叫做最小二乘法 (method of least square).其中 l� ‴ �‴� � ����� ���� �‴� � �� � ��� � � , h� ‴ � � l�� . h , l 的上方加 “ �� ”,表示是由观察值按最小二 乘法求得的估计值, l� 也叫回归系数. 回归分析 回归分析 回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法. 线性相关系数 对于变量 � 与变量 � 随机抽取到的 � 对数据 ����� , ����� , � , ����� ,利用相关系数 � 来衡量两个变量之间线性关系,相关系数的具体的计算公式为 � ‴ �‴� � �� � �� �� � � �‴� � �� � � � � �‴� � �� � � � � � 当 � ⸲ 〰 时,表明两个变量正相关,当 � 关 〰 时,表明两个变量负相关. ��� 越接近于 � ,表明 两个变量的线性相关性越强,当 ��� ⸲ 〰䁣�� 时,我们有 �‴〴 的把握认为两个变量之间具有线 性相关关系. ��� 接近于 〰 ,表明两个变量之间几乎不存在线性相关关系. 随机误差 (1)随机误差:在线性回归模型 � ‴ l� � h � 中, h 、 l 为模型的未知参数, 是 � 与 �� ‴ l� � h 之间的误差,通常 为随机变量,称为随机误差 (random error). 它的均值 � ‴ 〰 ,方差 � ‴ � � ⸲ 〰 .这样线性回归模型的完整表达式为 � ‴ l� � h � � � ‴ 〰�� ‴ � �䁣 回归方程 �� ‴ l�� � h� 中的 �� 是实际回归方程 �� ‴ l� � h 的一个估计量.由于随机误差为 ‴ � � �� ,所以 � ‴ � � �� 是 的估计量.(2)残差分析:对于样本点 ����� , ����� , � , ����� 而言,它们的随机误差为 � ‴ �� � l�� � h�� ‴ �������䁣 其估计值为 �� ‴ �� � ��� ‴ �� � l��� � h� , � ‴ � , � , � , � , �� 称为相应点 ����� 的残差 (residual).我们可以利用图形来分析残差特性.作图时纵坐标为残差,横坐标可以选为样 本编号,这样作出的图形为残差图.残差点比较均匀地落在水平的带状区域中,说明选用的模 型比较合适.这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越 高.还可以用 � � ‴ � � �‴� � ������ � � �‴� � ���� � � 来刻画回归的效果. � � 表达式中的 �‴� � �� � � � � 为确定的 数.因此 � � 越大,意味着残差平方和 �‴� � �� � �� � � � 越小,即模型的拟合效果越好; � � 越小, 残差平方和越大,即模型的拟合效果越差; � � 越接近于 � ,表示回归的效果越好. 独立性检验 独立性检验概念 取不同的“值”表示个体所属不同类别的变量称为分类变量.通过对样本的每个分类变量的 不同类别的事件发生的频率大小比较,来分析分类变量之间是否有关联关系. 如下表为 � � � 列联表: � � � 合计 � ��� ��� ��� � ��� ��� ���合计 ��� ��� �根据表中这 � 个数据来检验上述两种状态是否有关,这一检验问题就称为 � � � 列联表的独立 性检验. 独立性检验的基本思想 ①假设事件 �〰 为 � 与 � 没有关系,若 �〰 成立,即 � 与 � 没有关系,统计量 � � ‴ � ������ � ������ � ������������(有时 � � 也用 � � 来表示),用它的大小可以决定是否拒绝统计假设 �〰 ,如果算出的 � � 值较 大,就拒绝 � � ,也就是拒绝“事件 � 与 � 无关”,从而就认为它们是有关的了.②两个临界值: 䁣��� 与 �䁣�‴ .经过对 � � 统计量分布的研究,已经得到两个临界值: 䁣��� 与 �䁣�‴ .当根据 具体的数据算出的 � � ⸲ 䁣��� 时,有 �‴〴 的把握说事件 � 与 � 有关 ;当 � � ⸲ �䁣�‴ 时,有 ��〴 的把握说事件 � 与 � 有关.当 � � �䁣��� 时,认为事件 � 与 � 是无关. 精选例题 用样本估计总体 1. 总体平均数表示总体的 ,总体中位数表示总体的 ,总体方差表示总体 的 ,总体标准差表示总体的 . 【答案】 平均状态;中等水平;离散程度;离散程度 2. 若一组数据 ������������ 的总体方差是 � � ‴ � ��� �� � � �� � � � � ���� � � ��� ,则这组数据的 平均值为 . 【答案】 ��【分析】 设这个数据的个数为 � ,则 � ‴ � � �� � �� � � � �� � � � ‴ ���� � � ���� � ��� ���� � � �所以 � � ‴ �� � ��� � ����� � ��� ���������� ��� � � ‴ �� � ��� � ����� � ��� �� ��� � � ‴ �� � ��� � ����� � ��� � � ‴ � � �� � � �� � � � � �� � � � �䁣所以 � � ‴ ��� ,即 � ‴ �� . 3. 某校某年级有 �〰〰 名学生,已知这些学生完成家庭作业的时间均在区间 〰䁣‴� 内(单位: 小时),现将这 �〰〰 人完成家庭作业的时间分为 组: 〰䁣‴��䁣‴ , �䁣‴��䁣‴ , �䁣‴�䁣‴ 加以统 计,得到如图所示的频率分布直方图. 在这 �〰〰 人中,采用分层抽样的方法抽取 �〰 名学生研究其视力状况与完成作业时间的相关性, 则在抽取样本中,完成作业的时间小于 �䁣‴ 个小时的有 人. 【答案】 � 4. 为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为 �〰 的样本( �〰 名男 生的身高,单位: cm ),分组情况如下: 分组 �‴�䁣‴ � �‴�䁣‴ �‴�䁣‴ � ��‴䁣‴ ��‴䁣‴ � ��䁣‴ ��䁣‴ � ��䁣‴频数 � ��频率 h 〰䁣�则表中的 h ‴ . 【答案】 〰䁣�‴ 5. 数学课上,小明拿出了连续五日最低气温的统计表: 日期 一 二 三 四 五 最低气温 � C �� �� �� � �‴那么,这组数据的平均数和极差分别是 . 【答案】 �� , � 6. 某校从高一年级期末考试的学生中抽出 �〰 名学生,其成绩(均为整数)的频率分布直方图 如图所示. (1)估计这次考试的平均分. 【解】 利用组中值估算抽样学生的平均分: �‴ � �� � ‴‴ � �� � �‴ � � � ‴ � �� � �‴ � �‴ � �‴ � �� ‴ �‴ � 〰䁣〰‴ � ‴‴ � 〰䁣�‴ � �‴ � 〰䁣� � ‴ � 〰䁣 � �‴ � 〰䁣�‴ � �‴ � 〰䁣〰‴ ‴ � , 估计这次考试的平均分是 � 分. (2)假设在段 �〰��〰〰 的学生的成绩都不相同,且都在 �� 分以上,现用简单随机抽样方法, 从 �‴�������������〰〰 这个数中任取 � 个数,求这 � 个数恰好是两个学生的成绩的概率. 【解】 从 �‴�������������〰〰 中抽取 � 个数全部可能的基本结果有 �‴��� � �‴�� � �‴��� � �‴��� � �‴��〰〰 � ���� � ����� � ����� � ����〰〰 � ���� � ���� � ���〰〰 � ����� � ����〰〰 � ����〰〰 ,共 �‴ 个. 如果这 � 个数恰好是两个学生的成绩,则这 � 个学生在 �〰��〰〰 段,而 �〰��〰〰 的人数是 人,设这 人的成绩是 �‴����� ,则事件 � :" � 个数恰好是两个学生的成绩"包括的基本结 果有 �‴��� � �‴�� � ���� ,共有 个.所以所求的概率为 � � ‴ �‴ ‴ � ‴ . 7. 某大型养鸡厂, �〰〰〰〰 个鸡蛋能孵出 �‴� 只小鸡,根据概率的统计定义解答下列问题: (1)求这个养鸡场的鸡蛋孵化率; 【解】 这个养鸡场的鸡蛋孵化频率 �‴� �〰〰〰〰 ‴ 〰䁣�‴� , 它近似表示孵化率. (2) 〰〰〰〰 只鸡蛋大约能孵出多少只小鸡? 【解】 〰〰〰〰 只鸡蛋大约能孵出小鸡 〰〰〰〰 � 〰䁣�‴� ‴ �‴‴� (只). (3)若要孵出 ‴〰〰〰 只小鸡,大约需要多少只鸡蛋?(精确到百位) 【解】 要孵出 ‴〰〰〰 只小鸡, 大约需要鸡蛋 ‴〰〰〰��〰〰〰〰 �‴� � ‴� (只). 8. 设总体 ��������� 的平均数为 � ,方差为 �� ,求总体 ��� � l���� � l������ � l 的平均数和 方差(用 � 和 � 表示). 【解】 依题意得 � ‴ ���������� � � � ‴ ���� � � ���� � ��� ���� � � 所以 ��� � l���� � l������ � l 的平均数为 �� ‴ ����l � ����l ��� ����l � ‴ � ���������� ��l � ‴ �� � l ��� � l���� � l������ � l 的方差为 � � ‴ ����l ��� � � ����l ��� � ��� ����l ��� � � ‴ ����l � ���l � � ����l � ���l � ��� ����l � ���l � � ‴ � � � ���� � �� � � ���� � ���� � � ���� � � ‴ � � � �所以所求的平均数和方差分别为 �� � l 和 � � � � . 9. 有一组数据: ���������� �� 关 �� 关 � 关 �� 的算术平均值为 �〰 ,若去掉其中最大的一个, 余下数据的算术平均值为 � ;若去掉其中最小的一个,余下数据的算术平均值为 �� . (1)求出第—个数 �� 关于 � 的表达式及第 � 个数 �� 关于 � 的表达式; 【解】 依条件得 �� � �� � � � �� ‴ �〰� � �� � �� � � � �� � � ‴ � � � � � �� � � � � � �� ‴ �� � � � 由 � � � 得: �� ‴ � � � 又由 � � 得: �� ‴ �� � � . (2)若 ���������� 都是正整数,试求第 � 个数 �� 的最大值,并举出满足题目要求且 �� 取到最 大值的一组数据. 【解】 由于 �� 是正整数, 故 �� ‴ �� � ��� � �����〰 , 故 �� ‴ � � ���� , 当 ‴ �〰 时, �� ‴ � , ��〰 ‴ �� , �� � � � � � �� ‴ �〰 , 此时 �� ‴ � , � ‴ , �� ‴ � , �‴ ‴ � , �� ‴ �� , � ‴ �� , �� ‴ � , �� ‴ �� . 10. 为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽 出 �〰 名学生,将其成绩(成绩均为整数)分成六段 �〰�‴〰 , ‴〰��〰 , � , �〰��〰〰 后画出如 图的部分频率分布直方图,观察图形的信息,回答下列问题: (1)求第四小组的频率,并补全这个频率分布直方图; 【解】 因为各组的频率和等于 � , 故第四组的频率: �� ‴ � � 〰䁣〰�‴ � 〰䁣〰�‴ � � � 〰䁣〰� � 〰䁣〰〰‴ � �〰 ‴ 〰䁣 . 直方图如图所示. (2)估计这次考试的及格率( �〰 分及以上为及格)和平均分. 【解】 依题意,及格以上的分数所在的第三、四、五、六组的频率之和为 〰䁣〰�‴ � 〰䁣〰 � 〰䁣〰�‴ � 〰䁣〰〰‴ � �〰 ‴ 〰䁣‴ , 抽样学生成绩的合格率是 ‴〴 . 利用组中值估算抽样学生的平均分 �‴ � �� � ‴‴ � �� � �‴ � � � ‴ � �� � �‴ � �‴ � �‴ � �� ‴ �‴ � 〰䁣� � ‴‴ � 〰䁣�‴ � �‴ � 〰䁣�‴ � ‴ � 〰䁣 � �‴ � 〰䁣�‴ � �‴ � 〰䁣〰‴ ‴ �� 则估计这次考试的平均分是 � 分. 茎叶图 1. 如图茎叶图表示的是甲,乙两人在 ‴ 次综合测评中的成绩,其中一个数字被污损,则甲的 平均成绩超过乙的平均成绩的概率为 . 【答案】 � ‴【分析】 由已知中的茎叶图可得: 甲的 ‴ 次综合测评中的成绩分别为 �� , �� , �〰 , �� , �� . 则甲的平均成绩: � ‴ �� � �� � �〰 � �� � �� ‴ �〰 . 设污损数字为 � , 则乙的 ‴ 次综合测评中的成绩分别为 � , � , � , �� , �〰 � � . 则乙的平均成绩: � ‴ � � � � � � �� � �〰 � � ‴ ��䁣� � � ‴ , 当 � ‴ � ,甲的平均数 关 乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为 � �〰 , 当 � ‴ � ,甲的平均数 ‴ 乙的平均数,即乙的平均成绩等于甲的平均成绩的概率为 � �〰 , 甲的平均成绩超过乙的平均成绩的概率为 � � � �〰 � � �〰 ‴ � ‴ . 2. 以下茎叶图记录了某赛季甲、乙两名篮球运动员参加 �� 场比赛的得分(单位:分),若甲 运动员的中位数为 h ,乙运动员的众数为 l ,则 h � l 的值是 . 【答案】 � 【分析】 由图可知, h ‴ �� , l ‴ �� ,所以 h � l ‴ � . 3. 某校开展"爱我海西、爱我家乡"摄影比赛, � 位评委为参赛作品 � 给出的分数如茎叶图所示, 记分员在去掉一个最高分和一个最低分后,算得平均分为 �� ,复核员在复核时,发现有一个 数字(茎叶图中的 � )无法看清.若记分员计算无误,则数字 � 应该是 . � � � � � � � � � � � 【答案】 �【分析】 4. 从甲、乙两品种的棉花中各抽测了 �‴ 根棉花的纤维长度(单位: mm ),结果如下: 甲品种 � � � �� � ��〰 ��‴ ��‴ �� ��� ��� ��‴ 〰� 〰 〰 〰 〰� �〰 �� �� � �‴ �‴ �� � � ‴�乙品种 � � � ��� ��� ��‴ 〰� 〰� 〰 �� � �‴ �‴ �� �� �� �〰 �� �� �� � �� � � � ‴�由以上数据设计了如下茎叶图: 根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论: (1) ; (2) . 【答案】 (1)乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉 花的纤维长度普遍大于甲品种棉花的纤维长度). (2)甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度 较甲品种棉花的纤维长度更集中(稳定).或:甲品种棉花的纤维长度的分散程度比乙品种棉 花的纤维长度的分散程度更大). 【分析】 (3)甲品种棉花的纤维长度的中位数为 〰�mm ,乙品种棉花的纤维长度的中位 数为 ���mm . (4)乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(平均数附近).甲品种 棉花的纤维长度除一个特殊值 ‴� 外,也大致对称,其分布较均匀. 5. 如图是某校高二年级举办的歌咏比赛上,七位评委为某选手打出的分数的茎叶统计图,去 掉一个最高分和一个最低分后,所剩数据的方差为 . 【答案】 䁣� 6. 某良种培育基地正在培育一种小麦新品种 � ,将其与原有的一个优良品种 � 进行对照试验, 两种小麦各种植了 �‴ 亩,所得亩产数据(单位:千克)如下: 品种 �� ‴� ‴�� �� ��� ‴� ��� ��� ��� �〰〰� �〰‴� ���� ���� ��‴� ���� ��� ��� ��� �〰� �〰� ��� ��� ��‴� ��‴� �‴�� �‴� 品种 �� �� �� �� �� �‴� ��� ��� �� ��� ��� �‴� �� �� �〰〰� �〰�� �〰�� �〰� �〰�� �〰� ��〰� ���� ��‴� ���� ���� �〰(1)完成所附数据的茎叶图; 【解】 茎叶图如图所示: � � � ‴ � � ‴ � � � � ‴ � � � � � � � � ‴ ‴ 〰 �〰 〰 � � � ‴ � � �� 〰 � ‴ � � �� � � 〰 〰 � 〰 ‴ ‴ �� � � �‴ (2)用茎叶图处理现有的数据,有什么优点? 【解】 由于每个品种的数据都只有 �‴ 个,样本不大,画茎叶图很方便,此时茎叶图不仅 清晰明了地展示了数据的分布情况,便于比较,没有任何信息损失,而且还可以随时记录新的 数据. (3)通过观察茎叶图,对品种 � 与 � 的亩产量及其稳定性进行比较,写出统计结论. 【解】 通过观察茎叶图可以看出: (i)品种 � 的亩产平均数(或均值)比品种 � 高; (ii)品种 � 的亩产标准差(或方差)比品种 � 大,故品种 � 的亩产稳定性较差. 7. 某赛季甲、乙两名篮球运动员每场比赛得分情况如下: 甲的得分 � ��� �‴� ��� �‴� �� �� �� �� � �� ��� ��� ‴〰䁣乙的得分 � �� �� ��� ��� �� ��� ��� � �� �� ‴��试用茎叶图分析这两个人的成绩. 【解】 根据题意,把甲、乙两名篮球运动员的每场比赛得分情况,用茎叶图表示如下: 甲 乙 〰 � ‴ � � � � ‴ � � � � � � � � � � � � � � 〰 ‴ � 从这个茎叶图上可以看出,甲运动员的得分情况是大致对称的,中位数是 � ; 乙运动员的得分情况除一个特殊得分外,也大致对称,中位数是 �� . 因此甲运动员发挥比较稳定,总体得分情况比乙好. 8. 以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数 字模糊,无法确认,假设这个数字具有随机性,并在图中以 h 表示. 甲组 乙组 � � � � � 〰 � h(1)若甲、乙两个小组的数学平均成绩相同,求 h 的值; 【解】 依题意,得 � �� � �� � �� ‴ � �〰 � �� � �〰 � h ,解得 h ‴ � . (2)求乙组平均成绩超过甲组平均成绩的概率; 【解】 设“乙组平均成绩超过甲组平均成绩”为事件 � ,依题意 h ‴ 〰�������� ,共有 �〰 种 可能. 由(1)可知,当 h ‴ � 时甲、乙两个小组的数学平均成绩相同, 所以当 h ‴ �������� 时,乙组平均成绩超过甲组平均成绩,共有 � 种可能. 所以乙组平均成绩超过甲组平均成绩的概率 � � ‴ � �〰 ‴ � ‴ . 9. 如图所示的茎叶图的中间表示十位或百位数字,两边表示个位数字,回答下面的问题: (1)写出甲乙两组数据以及两组数据的中位数; 【解】 甲组: � , ‴ , � , �� , �� , � , �〰 , �〰� , �〰� , �〰� . 乙组: 〰 , �‴ , � , �� , �� , �� , �� , � , �〰〰 , �〰� . 甲组数据的中位数是 ���� � ‴ ��䁣‴ ,乙组数据的中位数是 ����� � ‴ ��䁣‴ . (2)通过茎叶图分析两组数据的稳定性,并且求其方差加以验证. 【解】 由茎叶图可以看出甲组数据较分散,乙组数据比较集中,因此乙组数据比较稳定. � 甲 ‴ �〰 � � �〰 � � �‴ � �� � �� � � � � � � � � �� � �� � �� ‴ �〰䁣� , � 乙 ‴ �〰 � � �〰 � � �〰 � � ‴ � � � � � � � � � � �� � �〰 ‴ �� , � � 甲 ‴ � �〰 � � �‴䁣� � � � ��䁣� � � � ��䁣� � � � �䁣� � � � �䁣� � � �䁣� � � ��䁣� � � �䁣� � � �‴䁣� � � �‴䁣� � ‴ �‴‴䁣�� , � � 乙 ‴ � �〰 � � �� � � � � � � � � � � 〰 � � � � � ‴ � � � � � 〰 � � �〰 � � � � ‴ 䁣� . 由于 � � 甲 ⸲ � � 乙,因此乙组的数据波动较小,比较稳定. 10. 对甲、乙两名自行车手在相同条件下进行了 � 次测试,测得他们的最大速度的数据如下表: 甲 � � 〰 ‴ �乙 �� � � �� �(1)画出茎叶图,由茎叶图你能获得哪些信息? 【解】 画茎叶图如图所示: 甲 乙 � � � � ‴ � 〰 � � �从这个茎叶图可以看出,甲、乙的得分情况都是均匀分布的,只是乙成绩更好些;乙的中位 数是 䁣‴ ,甲的中位数是 . (2)分别求出甲、乙两名自行车手最大速度数据的平均数、标准差、并判断选谁参加比赛更 合适. 【解】 根据表中数据得 � 甲 ‴ , � 乙 ‴ , � 甲 � � 䁣�� , � 乙 � � 䁣‴� ,比较可知,选乙参 加比赛比较合适. 样本数据的数字特征 1. 抽样统计甲、乙两个城市连续 ‴ 天的空气质量指数( ��� ),数据如下: 则空气质量指数(AQI)较为稳定(方差较小)的城市为 (填‘‘甲”或“乙”). 【答案】 乙 【分析】 因为 � 甲 ‴ � 乙 ‴ ��� , 所以 � 甲 � ‴ � ‴ �〰� � ��� � � ��� � ��� � � �� � ��� � � ��� � ��� � � ��〰 � ��� � ‴ � , � 乙 � ‴ � ‴ ��〰 � ��� � � ��� � ��� � � ��‴ � ��� � � �� � ��� � � ��� � ��� � ‴ ��䁣� , 所以 � 乙 � 关 � 甲 � . 2. —组数据从小到大排列后,如果第 �� 个数和第 ‴〰 个数的平均数是这组数据的中位数,则 该组数据 共有 个数. 【答案】 �� 3. 某老师从星期一到星期五收到信件数分别是 �〰 , � , � , ‴ , � ,则该组数据的方差 � � ‴ . 【答案】 �� ‴ 4. 某市连续 ‴ 天测得空气中的 PM2.5(直径小于或等于 2.5 微米的颗粒物)的数据(单位; μg/m )分别为 ��‴ , ��‴ , �� , ��� , ��‴ ,则该组数据的方差为 . 【答案】 �䁣� (写成 �‴� ‴ 也对) 【分析】 因为 � ‴ �‴� � ��� ‴ ��〰 � �‴�‴������‴ ‴ ‴ ��‴ , 所以 � � ‴ �‴� � �� � � � � ‴ �〰 � �〰� � � � �〰 ‴ ‴ �‴� ‴ ‴ �䁣� . 5. 由正整数组成的一组数据 ���������� ,其平均数和中位数都是 � ,且标准差等于 � ,则这组 数据为 .(从小到大排列) 【答案】 �����【解】 设 ���������� ,则得 �� � � ‴ ����� � �� � � � �� ‴ �䁣 所以 �� � �� ‴ � ,故 ��� .因为 � � ‴ � ,所以 �� � � � � �� � � � � � � � � � �� � � � ‴ �䁣 因为 ��� ,所以只能取 �� � � ‴ � ,得这组数据为 ����� . 6. 某公司有 �‴ 名员工,他们所在部门及相应每人所创利润如下表所示(单位:万元): 部门 � � � � � � �人数 � � � � � � 利润 �〰 ‴ �䁣‴ �䁣� �䁣‴ �䁣‴ �䁣� (1)求该公司每人所创年利润的平均数和中位数; 【解】 � ‴ ���〰���‴����䁣‴�����䁣� �‴ ‴ 䁣� (万元); 中位数为 �䁣� 万元. (2)你认为使用平均数和中位数哪一个来描述该公司每人所创年利润的一般水平比较合理? 【解】 因该公司 � 部门每人所创年利润与其他部门每人所创年利润差距很大,导致平均数 与中位数偏差很大,所以应用中位数来描述该公司每人所创年利润一般水平比较合理. 7. 为了了解 ��� 两种轮胎的性能,某汽车制造厂分别从这两种轮胎中随机抽取了 � 个进行测 试,下面列出了每一个轮胎行驶的最远路程数(单位: �〰〰〰�km ): 轮胎 ������������〰���〰〰��〰������轮胎 ���〰���〰������〰‴���������〰�(1)分别计算 ��� 两种轮胎行驶最远路程的平均数; 【解】 �� ‴ �〰〰��� ‴ �〰〰 ; (2)分别计算 ��� 两种轮胎行驶最远路程的极差、标准差. 【解】 � 轮胎的极差为 ��� � �� ‴ ���� 轮胎的极差为 �〰� � � ‴ �‴ . �� � 䁣���� � ‴䁣� . 8. 某学校高一( � )班和高一( � )班各有 �� 名学生,两班在一次数学测验中的成绩统计如下: 班级 平均分 众数 中位数 标准差 � 班 � 〰 � ��䁣� � 班 � 〰 � ‴䁣� (1)请你对下面的一段话给予简要分析: 高一( � )班的小刚回家对妈妈说:" 昨天的数学测验,全班平均分为 � 分,得 〰 分的人 最多,我得了 �‴ 分,在班里算上上游了!" 【解】 由于(1)班 �� 名学生数学测验成绩的中位数是 � ,则 �‴ 分排在全班第 �‴ 名之 后,所以从位次上看,不能说 �‴ 分是上游,成绩应该属于中游. 但也不能以位次来判断学习的好坏,小刚得了 �‴ 分,说明他对这段的学习内容掌握得较好, 从掌握学习的内容上讲,也可以说属于上游. (2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议. 【解】 (1)班成绩的中位数是 � 分,说明高于 � 分(含 � )的人数占一半以上,而平 均分为 � 分,标准差又很大,说明低分也多,两极分化严重,建议加强对学习困难的学生的 帮助. (2)班的中位数和平均数都是 � 分,标准差又小,说明学生之间差别较小,学习很差的学 生少,但学习优异的也很少,建议采取措施提高优秀率. 9. 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随 机抽取 � 次,记录如下: 甲: �� , �� , � , � , �‴ , �� , � , ��乙: �� , �‴ , �〰 , ‴ , � , �〰 , �〰 , �‴(1)用茎叶图表示这两组数据; 【解】 作出茎叶图如下. 甲 乙 � � ‴ � � � � � 〰 〰 ‴ ‴ � 〰 � ‴ (2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个) 考虑,你认为选派哪位学生参加合适?请说明理由. 【解】 根据所给的数据得到, � 甲 ‴ � � � � � � �� � �� � �� � �� � � � �‴ ‴ �‴ , � 乙 ‴ � � ‴ � �〰 � �〰 � � � �‴ � �〰 � �� � �‴ ‴ �‴ , � 甲 � ‴ � � � � �‴ � � � � �‴ � � �� � �‴ � � �� � �‴ � � �� � �‴ � � �� � �‴ � � � � �‴ � � �‴ � �‴ � ‴ ‴䁣‴ , � 乙 � ‴ � � ‴ � �‴ � � �〰 � �‴ � � �〰 � �‴ � � � � �‴ � � �‴ � �‴ � � �〰 � �‴ � � �� � �‴ � � �‴ � �‴ � ‴ �� . � � 甲 ‴ � 乙, � 甲 � 关 � 乙 � , � 甲的成绩较稳定,派甲参赛比较合适. 10. 已知一组数据按从小到大的顺序排列为 � � , 〰 , � , � , , �� ,中位数为 ‴ ,求这组数据 的平均数和方差. 【解】 由 ��� � ‴ ‴ ,得 � ‴ � , � � ‴ ‴ , � � ‴ ��䁣 . 变量间的相关关系 1. 甲、乙、丙、丁四位同学各自对 ��� 两个变量的线性相关性做实验,并用回归分析方法分 别求得相关系数 � 与残差平方和 � 如下表: 甲 乙 丙 丁 � 〰䁣�� 〰䁣� 〰䁣�� 〰䁣�‴ � �〰� ��‴ ��� �〰则在这四位同学中, 同学的试验结果体现 ��� 两个变量有更强的线性相关性. 【答案】 � 2. 若两个分类变量 � 与 � 的列联表为: �� �� 总计 �� �〰 �‴ �‴ �� �〰 �� ‴�总计 ‴〰 � ��则“ � 与 � 之间有关系”这个结论出错的概率为 . 【答案】 〰䁣〰�【分析】 由 � � � 列联表,可求得随机变量 � � 的值为 � � ‴ ��� �〰�����〰��‴ � �‴�‴��‴〰�� � 䁣�� ⸲ �䁣�‴ . 因为 � � � ��䁣�‴ � 〰䁣〰� , 所以“ � 与 � 之间有关系”出错的概率仅为 〰䁣〰� . 3. 报载,中国的青少年在最近几年的体质情况逐年下降,某高校调查询问了 ‴� 名男女大学生, 在课余时间是否参加运动,得到下表所示的数据,从表中数据分析,认为大学生的性别与参加 运动之间有关系的把握有 〴 . 参加运动 不参加运动 合计 男大学生 �〰 � ��女大学生 �� �� ��合计 � �� ‴�【答案】 �‴ 4. 某商品在 ‴ 家商场的售价 � (元)和销售量 � (件)之间的一组数据如下表所示: 价格 � 元 � �䁣‴ �〰 �〰䁣‴ ��销售量 � 件 �� h � � ‴由散点图可知,销售量 � 与价格 � 之间有较好的线性相关关系,且回归直线方程是 �� ‴� 䁣�� � �h ,则 h ‴ . 【答案】 �〰【分析】 根据题意得, � ‴ ���䁣‴��〰��〰䁣‴��� ‴ ‴ �〰 , � ‴ ���h�����‴ ‴ ‴ h ‴ � � , 因为回归直线过样本中心点 ��� , 所以 h ‴ � � ‴� 䁣�� � �h , 解得 h ‴ �〰 . 5. 已知样本容量为 �� ,计算得 �‴� �� ��� ‴ ‴�〰 , �‴� �� �� ‴ ���� ,回归方程为 �� ‴ 〰䁣� � h� ,则 � � , h� � .(精确到 〰䁣〰� ) 【答案】 ��䁣� ; ‴䁣‴‴ 6. 在研究色盲与性别的关系调查中,调查了男性 ��〰 人,其中有 � 人患色盲,调查的 ‴�〰个女性中 � 人患色盲,根据以上的数据得到一个 � � � 的列联表如下 患色盲 不换色盲 总计 男 ��〰女 ‴�〰总计 �〰〰〰(1)请根据以上的数据完成这个 � � � 的列联表; 【答案】 患色盲 不换色盲 总计 男 � ��� ��〰女 � ‴�� ‴�〰总计 �� �‴� �〰〰〰 【解】 患色盲 不换色盲 总计 男 � ��� ��〰女 � ‴�� ‴�〰总计 �� �‴� �〰〰〰 (2)若认为“性别与患色盲有关系”,则出错的概率会是多少? 参考数据: ��‴�������� � ��〰�‴�〰�����‴� ‴ 〰䁣〰���� ��������‴�� � ��〰�‴�〰�����‴� ‴ �䁣�〰���� ��������‴�� � ��〰�‴�〰�����‴� ‴ 〰䁣〰���� 【答案】 出错的概率为 〰䁣〰〰� . 【解】 假设 � :“性别与患色盲没有关系”. 先算出 � 的观测值: � ‴ �〰〰〰 � � � ‴�� � ��� � � � ��〰 � ‴�〰 � �� � �‴� ‴ �䁣��则有 � � � ��〰䁣�〰� ‴ 〰䁣〰〰� 即是 � 成立的概率不超过 〰䁣〰〰� , 若认为“性别与患色盲有关系”,则出错的概率为 〰䁣〰〰� . 7. 一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格: 人数 �i �〰 �‴ �〰 �‴ 〰 ‴ �〰件数 �i � �� �‴ �〰 � �其中 i ‴ � , � , , � , ‴ , � , . (参考公式: l� ‴ i‴� � �i�i� ���� i‴� � �i � � ��� � , h� ‴ � � l�� ) 参考数据: i‴� �i�i� ‴ ��‴ , � ‴ �‴ , � ‴ �‴䁣� , i‴� �i � � ‴ ‴〰‴ , � � ‴ �‴ , �� ‴ �〰〰(1)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图; 【解】 散点图如图: (2)求回归直线方程;(结果四舍五入后保留到小数点后两位) 【解】 因为 i‴� �i�i� ‴ ��‴ , � ‴ �‴ , � ‴ �‴䁣� , i‴� �i � � ‴ ‴〰‴ , � � ‴ �‴ , �� ‴ �〰〰 , 所以 l� ‴ i‴� � �i�i� ���� i‴� � �i � � ��� � ‴ ��‴��〰〰 ‴〰‴��‴ � 〰䁣� , h� ‴ � � l�� ‴� �䁣� , 所以回归直线方程是 �� ‴ 〰䁣�� � �䁣� . (3)预测进店人数为 �〰 人时,商品销售的件数.(结果保留整数) 【解】 进店人数为 �〰 人时,商品销售的件数 � ‴ 〰䁣� � �〰 � �䁣� � ‴� . 8. 为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了 ‴〰〰 位 老年人,结果如下: 附: � � � �� 〰䁣〰‴〰 〰䁣〰�〰 〰䁣〰〰� � 䁣��� �䁣�‴ �〰䁣��� � � ‴ � h݀�l� � h�l ��݀ h�� l�݀(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例; 【解】 调查的 ‴〰〰 位老年人中有 〰 位需要志愿者提供帮助,因此该地区老年人中,需要 帮助的老年人的比例的估算值为 〰 ‴〰〰 ‴ ��〴 . (2)能否有 ��〴 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关? 【解】 � � ‴ ‴〰〰 �〰��〰�〰���〰 � �〰〰�〰〰�〰��〰 ‴ �䁣�� , 由于 �䁣�� ⸲ �䁣�‴ ,所以有 ��〴 的把握认为该地区的老年人是否需要帮助与性别有关. (3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿者帮助的老 年人的比例?说明理由. 【解】 由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看 出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地 区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽 样方法更好. 9. 为了比较注射 A,B 两种药物后产生的皮肤疱疹的面积,选 �〰〰 只家兔做试验,将这 �〰〰只家兔随机地分成两组,每组 �〰〰 只,其中一组注射药物 A,另一组注射药物 B.下表 1 和表 2 分别是注射药物 A 和药物 B 的试验结果.(疱疹面积单位: mm � ) 表 1:注射药物 A 后皮肤疱疹面积的频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰频数 〰 �〰 �〰 �〰表 2:注射药物 B 后皮肤疱疹面积的频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰 �〰��‴频数 �〰 �‴ �〰 〰 �‴附: � � ‴ � h݀�l� � h�l ��݀ h�� l�݀ � � � �� 〰䁣�〰〰 〰䁣〰‴〰 〰䁣〰�‴ 〰䁣〰�〰 〰䁣〰〰� � �䁣〰� 䁣��� ‴䁣〰�� �䁣�‴ �〰䁣���(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小; 【答案】 直方图略,注射药物 A 后疱疹面积的中位数小于注射药物 B 后疱疹面积的中位 数 【解】 可以看出注射药物 A 后的疱疹面积的中位数在 �‴ 至 〰 之间, 而注射药物 B 后的疱疹面积的中位数在 〰 至 ‴ 之间, 所以注射药物 A 后疱疹面积的中位数小于注射药物 B 后疱疹面积的中位数. (2)完成下面 � � � 列联表,并回答能否有 ��䁣�〴 的把握认为“注射药物 A 后的疱疹面积与注 射药物 B 后的疱疹面积有差异”. 表 3: 疱疹面积小于 �〰�mm � 疱疹面积不小于 �〰�mm � 合计 注射药物 �� h ‴ l ‴注射药物 �� � ‴ ݀ ‴合计 � ‴ 【答案】 列联表略,有 ��䁣�〴 的把握认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱 疹面积有差异” 【解】 表 疱疹面积小于 �〰�mm � 疱疹面积不小于 �〰�mm � 合计 注射药物 �� h ‴ 〰 l ‴ 〰 �〰〰注射药物 �� � ‴ ‴ ݀ ‴ �‴ �〰〰合计 �〰‴ �‴ � ‴ �〰〰 � � ‴ �〰〰 � 〰 � �‴ � ‴ � 〰 � �〰〰 � �〰〰 � �〰‴ � �‴ � ��䁣‴�䁣由于 � � ⸲ �〰䁣���� 所以有 ��䁣�〴 的把握认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱疹面积有差异”. 10. 假设关于某设备的使用年限 � 和支出的维修费用 � (万元),有如下表的统计资料: 使用年限 � � ‴ �维修费用 �䁣� 䁣� ‴䁣‴ �䁣‴ 䁣〰由资料说明, � 对 � 具有线性相关关系,试求 � 对 � 的线性回归方程. 【解】 设 � 对 � 的线性回归方程为 �� ‴ l�� � h� ,由题可知, l� ‴ i‴� ‴ �i�i� �‴�� i‴� ‴ �i � � �‴� � ‴ ���䁣�‴���‴ �〰�‴�� � ‴ �䁣�䁣 h� ‴ � � l�� ‴ ‴ � �䁣� � � ‴ 〰䁣〰� . 所以线性回归方程为 �� ‴ �䁣�� � 〰䁣〰� . 线性回归方程 1. 在研究硝酸钠的可溶性程度时,对不同的温度观测它在水中的溶解度,得观测结果如下: 温度 � 〰 �〰 �〰 ‴〰 〰溶解度 � ��䁣 �䁣〰 �‴䁣〰 ���䁣 ���䁣〰则由此得到的回归直线方程为 . 【答案】 �� ‴ 〰䁣��〰�� � �䁣� 2. 在两个变量的回归分析中,作散点图的目的是 【答案】 观察它们之间是否存在线性关系 3. 某工厂经过技术改造后,生产某种产品的产量 � (吨)与相应的生产能耗 � (吨标准煤)有 如下几组样本数据: � � ‴ � � �䁣‴ � �䁣‴根据相关性检验,这种样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率 为 〰䁣 ,那么这组样本数据的回归直线方程是 . 【答案】 �� ‴ 〰䁣� � 〰䁣‴【分析】 根据样本数据,得 � ‴ �䁣‴ , � ‴ 䁣‴ . 设回归直线方程为 �� ‴ 〰䁣� � h� ,所以 h� ‴ � � 〰䁣� ‴ 〰䁣‴ . 因此,回归直线方程为 �� ‴ 〰䁣� � 〰䁣‴ . 4. 某农场粮食产量的统计结果如图所示,从图中我们可以看到前 � 年的粮食总产量 �� 与 � 之 间的关系.则从目前的统计结果来看,前 年的年平均粮食产量最高. 【答案】 5. 在国家宏观政策的调控下,中国经济已经走向复苏.统计我市某小型企业在 �〰�〰 年 � � ‴月的收入,得到月份 � (月)与收入 � (万元)的情况如下表: 月份 � � � � ‴收入 � ��〰 �〰 �‴〰 ��〰 ��〰则 � 关于 � 的回归直线方程为 . 【答案】 � ‴ �� � ��【分析】 � ‴ , � ‴ �‴〰 , l� ‴ � , h� ‴ � � l�� ‴ �� . 6. 一般说来,一个人的身高越高,他的手就越大.为调查这一问题,对 �〰 名高三男生的身高 与右手一扎长测量,得到如下一组数据(单位: cm ). 身高 ��� �〰 �� �� �� �� �� �� ��〰 ���一扎长 ��䁣〰 �〰䁣〰 ��䁣〰 ��䁣‴ ��䁣〰 ��䁣〰 ��䁣〰 �䁣〰 ��䁣‴ �䁣〰其中 �‴� �〰 �� � � ‴ 〰‴〰 , �‴� �〰 ��� �� ‴ ��� . (1)画出散点图,你能发现两者有相关关系吗? 【解】 散点图如下: 由散点图可以发现,身高与右手一扎长之间的总体趋势成一条直线,所以它们线性相关. (2)如果有相关关系,求回归直线方程. 【解】 设回归直线方差为 �� ‴ l� � h ,由题意可得 � ‴ ��䁣� , � ‴ ��䁣 . 又 �‴� �〰 �� � � ‴ 〰‴〰 , �‴� �〰 ��� �� ‴ ��� . � l� � 〰䁣〰 , h� ‴ � � l�� ‴� �䁣��� ,因此回归直线方程为 �� ‴ 〰䁣〰� � �䁣��� . 7. 一台还可以用的机器由于使用的时间较长,它按不同的转速生产出来的某机械零件有一些 会有缺陷,每小时生产有缺陷零件的多少随机器运转的速率而变化,下表为抽样试验结果: 转速 � 转 / 秒 �� �� �� �每小时生产有缺陷的零件数 � 件 �� � � ‴(1)画出散点图; 【解】 画出散点图,如图所示. (2)如果 � 与 � 有线性相关的关系,求回归直线方程; 【解】 � ‴ ��䁣‴ , � ‴ �䁣�‴ , � l ‴ �������䁣‴��䁣�‴ ��〰�����䁣‴ � � 〰䁣��� , h ‴� 〰䁣�‴‴ . � 回归直线方程为 � ‴ 〰䁣���� � 〰䁣�‴‴ . (3)机器的转速应控制在多少转/秒?可使每小时生产有缺陷的零件数不多于 �〰 个; 参考公式:线性回归方程系数公式开始 l� ‴ �‴� � ��� ������� �‴� � �� � � ��� � , h� ‴ � � l�� . 【解】 要使 ���〰 ,则 〰䁣���� � 〰䁣�‴‴��〰 , ����䁣�〰�� . 故机器的转速应控制在 ��䁣� 转/秒以下. 8. 某公司近年来科研费用支出 � 万元与公司所获得利润 � 万元之间有如下的统计数据: � � � ‴ � �� � � ‴(1)请根据上表提供的数据,用最小二乘法求出 � 关于 � 的线性回归方程 �� ‴ l�� � h� ; 【解】 � ‴ �����‴ � ‴ 䁣‴ , � ‴ �������‴ � ‴ �� , �‴� � ��� �� ‴ � � �� � � � � � � � � ‴ � ‴ ‴ ��〰 , �‴� � � � � ‴ � � � � � � � � ‴ � ‴ ‴� , l� ‴ �‴� � ��� ������ �‴� � �� � � �� � � ‴ ��〰���䁣‴��� ‴����䁣‴ � ‴ ‴䁣� . h� ‴ � � l�� ‴ �� � ‴䁣� � 䁣‴ ‴ �䁣� , 所以回归方程为 �� ‴ ‴䁣�� � �䁣� . (2)试根据(2)求出的线性回归方程,预测该公司科研费用支出为 �〰 万元时公司所获得的 利润. 参考公式:若变量 � 和 � 用最小二乘法求出 � 关于 � 的线性回归方程为: �� ‴ l�� � h� ,其中: l� ‴ �‴� � ��� ������ �‴� � �� � � �� � � , h� ‴ � � l�� ,参考数值: � � �� � � � � � � � � ‴ � ‴ ‴ ��〰 . 【解】 当 � ‴ �〰 时, � ‴ ‴䁣� � �〰 � �䁣� ‴ ��䁣� (万元), 故预测该公司科研费用支出为 �〰 万元时公司所获得的利润为 ��䁣� 万元. 9. 为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议,现对他前 次 考试的数学成绩 � 、物理成绩 � 进行分析.下面是该生 次考试的成绩: 数学 �� � �� �� �〰� �〰〰 ���物理 �� �� �〰� �� �〰� �〰� �〰�(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明; 【解】 � ‴ �〰〰 � �������������� ‴ �〰〰 ; � ‴ �〰〰 � �������������� ‴ �〰〰 ; 因此, � 数学 � ‴ ��� ‴ ��� , � 物理 � ‴ �‴〰 , 从而 � 数学 � ⸲ � 物理 � ,所以物理成绩更稳定. (2)已知该生的物理成绩 � 与数学成绩 � 是线性相关的,若该生的物理成绩达到 ��‴ 分,请 你估计他的数学成绩大约是多少.并请你根据物理成绩与数学成绩的相关性,给出该生在学习 数学、物理上的合理性建议. 【解】 由于 � 与 � 之间具有线性相关关系,根据回归系数公式得到 l ‴ �‴� ��� ����� �‴� �� � � �� � ‴ �� ��� ‴ 〰䁣‴ , h ‴ � � l� ‴ �〰〰 � 〰䁣‴ � �〰〰 ‴ ‴〰 , 因此回归直线方程为 � ‴ 〰䁣‴� � ‴〰 . 当 � ‴ ��‴ 时, � ‴ �〰 ,即该生物理成绩达到 ��‴ 分时,他的数学成绩大约为 �〰 分. 建议:进一步加强对数学的学习,提高数学成绩的稳定性,将有助于物理成绩的进一步提高. 10. 假设关于某设备的使用年限 � 和所支出的维修费用 � (万元)有如下的统计资料: 使用年限 � � � ‴ �维修费用 � �䁣� 䁣� ‴䁣‴ �䁣‴ 䁣〰若由资料知 � 对 � 呈线性相关关系. (1)请画出上表数据的散点图; 【解】 (2)请根据最小二乘法求出线性回归方程 �� ‴ l� � h 的回归系数 h , l ; l ‴ �‴� � ����� ����� �‴� � �� � ��� � � , h ‴ � � l� 【解】 �� ‴ �䁣�� � 〰䁣〰� ; (3)估计使用年限为 �〰 年时,维修费用是多少? 【解】 ��䁣� 万元. 回归分析 1. 样本相关系数 � 满足 � �� 且 � 越接近 � ,线性相关程度越 , � 越接近 〰 ,线性 相关程度越 【答案】 强;弱 2. 为了考察两个变量 � 与 � 的线性相关性,测得 � , � 的 � 对数据,若 � 与 � 具有线性相关 关系,则相关系数 � 的取值范围是 . 【答案】 〰䁣‴‴�� 3. 若有一组数据的总偏差平方和为 �〰〰 ,相关指数为 〰䁣‴ ,则其残差平方和为 ,回 归平方和为 . 【答案】 ‴〰�‴〰 【分析】 根据公式 � � ‴ � � 残差平方和 总偏差平方和 ,得残差平方和为 ‴〰 ,从而回归平方和为 �〰〰 � ‴〰 ‴ ‴〰 . 4. 在分析两个分类变量之间是否有关系时,常用到的图表有 . 【答案】 列联表、三维柱形图、二维条形图 5. 线性回归模型中 � ‴ l� � h � , l ‴ , h ‴ . 【答案】 �‴� � ����� ���� �‴� � ���� � � ; � � l� 6. 已知 � , � 之间的一组数据如下表: � � � � � � � � ‴对于表中数据,甲、乙两同学给出的拟合直线分别为 � ‴ � � � � 与 � ‴ � � � � � � ,试利用"最小 二乘法"判断哪条直线拟合程度更好. 【解】 用 � ‴ � � � � 作为拟合直线时,所得 � 值与 � 的实际值的差的平方和为 �� ‴ � � � � � � � � � � � � � �〰 � � � � �� � ‴ � ‴ �用 � ‴ � � � � � � 作为拟合直线时,所得 � 值与 � 的实际值的差的平方和为 �� ‴ � � � � � � � � � � � � � � � � � � � � � � ‴ � ‴ � � � �� 关 �� ,故用直线 � ‴ � � � � � � 拟合程度更好. 7. 某种产品表面进行腐蚀试验,得到腐蚀深度 � 与腐蚀时间 � 之间对应的一组数据: 时间 �/s ‴ �〰 �‴ �〰 〰 �〰 ‴〰 �〰 〰 �〰 ��〰深度 �/�m � �〰 �〰 � �� � �� � �‴ �� ��试求 � 对 � 的回归方程,并判断 � 与 � 之间的线性相关关系有无统计意义(可靠性不低于 �‴〴 ). 【解】 根据公式可以求得 � 对 � 的回归方程为 �� ‴ ‴䁣��� � 〰䁣〰�� . � 与 � 之间的线性相关关系具有统计意义(可靠性不低于 �‴〴 ). 检验过程如下: ①统计假设 �〰 :变量 � 与 � 之间不具有线性相关关系; ②以 �‴〴 的把握作出推断,根据 � � 〰䁣�‴ ‴ 〰䁣〰‴ 与 � � � ‴ �� � � ‴ � ,在教材附录中查 得 � 的临界值 �〰䁣〰‴ ‴ 〰䁣�〰� ; ③计算相关系数得 � � 〰䁣���〰 ; ④因为 〰䁣���〰 ⸲ 〰䁣�〰� ,统计假设 �〰 不成立,所以,我们有 �‴〴 以上的把握认为这个线性 相关关系具有统计意义. 8. 假设关于某种设备的使用年限 � (年)与所支出的维修费用 � (万元)有如下统计资料: � � � ‴ � � �䁣� 䁣� ‴䁣‴ �䁣‴ 䁣〰已知 �‴� ‴ �� � � ‴ �〰 , �‴� ‴ �� � � ‴ ��〰䁣� , �‴� ‴ ��� �� ‴ ���䁣 , � � �䁣� , � � �䁣� . (1)求 � , � ; 【答案】 � ‴ � , � ‴ ‴【解】 � ‴ �����‴�� ‴ ‴ � , � ‴ �䁣��䁣��‴䁣‴��䁣‴�䁣〰 ‴ ‴ ‴ . (2)对 � , � 进行线性相关性检验; 【答案】 � 与 � 之间具有线性相关关系 【解】 �‴� ‴ ����� � ‴�� ‴ ���䁣 � ‴ � � � ‴ ‴ ��䁣 , �‴� ‴ �� � � � ‴� � ‴ �〰 � ‴ � � � ‴ �〰 , �‴� ‴ �� � � � ‴� � ‴ ��〰䁣� � ��‴ ‴ �‴䁣� , � � ‴ ��䁣 �〰��‴䁣� ‴ ��䁣 �‴� � 〰䁣�� . � � ⸲ 〰䁣‴ , 所以认为 � 与 � 之间具有线性相关关系,求线性回归方程是有意义的. (3)如果 � 与 � 具有线性相关关系,求出线性回归方程; 【答案】 �� ‴ �䁣�� � 〰䁣〰�【解】 l� ‴ �‴� ‴ ����� �‴�� �‴� ‴ �� � � �‴� � ‴ ��䁣 �〰 ‴ �䁣� , h� ‴ � � l�� ‴ ‴ � �䁣� � � ‴ 〰䁣〰� , 所以线性回归方程为 �� ‴ �䁣�� � 〰䁣〰� . (4)估计使用年限为 �〰 年时,维修费用约是多少? 【答案】 ��䁣� 万元 【解】 当 � ‴ �〰 时, �� ‴ �䁣� � �〰 � 〰䁣〰� ‴ ��䁣� (万元),即估计使用年限为 �〰 年时, 维修费用约为 ��䁣� 万元. 9. �〰 名同学在高一年级时和高二年级时的数学平均成绩如下表: � � � � �� � � 〰 �‴ � � � ‴ � 〰 � � �‴ �� � 其中 � 为高一年级时数学平均成绩, � 为高二年级时数学平均成绩.试问:这 �〰 个学生的两 次数学考试成绩是否具有显著性线性相关关系? 【解】 判断两变量之间是否具有相关关系,首先要求出其相关系数 � ,依据 � 越接近 � , 表明这两个变量的相关性越强; � 越接近 〰 ,表明两个变量之间几乎不存在线性相关关系. 由已知表格中所给数据,利用科学计算器进行计算,得: � ‴ � , � ‴ �䁣 , �‴� �〰 ��� ‴ �〰 , �‴� �〰 ��� ‴ � , �‴� �〰 ��� �� ‴ ‴��� , �‴� �〰 �� � � ‴ ‴〰‴�〰 , �‴� �〰 �� � � ‴ ‴�‴�� . 于是 � ‴ ‴������� ‴〰‴�〰��〰��� ‴�‴����〰��䁣� � 〰䁣� . � � ⸲ 〰䁣‴ , � � 与 � 具有很强的线性相关关系. 10. 关于两个变量 � 和 � 的 组数据如下表所示: � �� � �‴ � �� � ‴ � �� �� �� �� ��‴ �‴试判断 � 与 � 之间是否有线性相关关系? 【解】 � ‴ � �� � � � �‴ � � � �� � � � ‴ � �䁣� , � ‴ � � � �� � �� � �� � �� � ��‴ � �‴ � ��䁣 , �‴� �� � � ‴ �� � � � � � �‴ � � � � � �� � � � � � ‴ � ‴ ‴��� , �‴� ��� �� ‴ �� � � � � �� � �‴ � �� � � � �� � �� � �� � � � ��‴ � ‴ � �‴ ‴ ��‴�� . �‴� �� � � ‴ � � �� � � �� � � �� � � �� � � ��‴ � � �‴ � ‴ ���� , � ‴ �‴� ��� ����� �‴� �� � � �� � �‴� �� � � �� � ‴ ��‴�����䁣����䁣 ‴������䁣�� � ��������䁣� � 〰䁣�‴䁣由于 � ‴ 〰䁣�‴ ⸲ 〰䁣‴ , � � 与 � 具有线性相关关系. 独立性检验 1. 某医疗研究所为了检验某种血清预防感冒的作用,把 ‴〰〰 名使用血清的人与另外 ‴〰〰 名未 使用血清的人一年中的感冒记录作比较,提出假设 �〰 :“这种血清不能起到预防感冒的作用”, 利用 � � � 列联表计算得 � � � 䁣��� ,经查临界值表知 � � � �䁣��� � 〰䁣〰‴ .则下列结论中, 正确结论的序号是 ① 有 �‴〴 的把握认为“这种血清能起到预防感冒的作用”; ② 若某人未使用该血清,那么他在一年中有 �‴〴 的可能性得感冒; ③ 这种血清预防感冒的有效率为 �‴〴 ; ④ 这种血清预防感冒的有效率为 ‴〴 . 【答案】 ① 【分析】 � � � 䁣��� ⸲ 䁣��� ,而 � � � �䁣��� � 〰䁣〰‴ ,所以有 �‴〴 的把握认为“这种血清 能起到预防感冒的作用”;但检验的是假设是否成立和该血清预防感冒的有效率是没有关系的, 不是同一个问题,不要混淆,正确序号为 ①. 2. 某校要研究学生近视情况是否与性别有关,你认为应该收集哪些数据? . 【答案】 男生近视人数,男生不近视人数,女生近视人数,女生不近视人数 3. 对 ��� 个接受心脏搭桥手术的病人和 ��� 个接受血管清障手术的病人进行了 年的跟踪研 究,调查他们是否又发作过心脏病,调查结果如下表所示: � 又发作过心脏病 未发作过心脏病 合计 心脏搭桥手术 � �‴ ���血管清障手术 �� �� ���合计 �� �� ��试根据上述数据计算 � � ‴ (结果精确到 〰䁣〰� ),比较这两种手术对病人又发作心脏病 的影响有没有差别 . 【答案】 �䁣� ;不能作出这两种手术对病人又发作心脏病的影响有差别的结论 4. 针对两个分类变量做独立性检验,若 � � 统计量的值越大,则说明这两个分类变量间有关系 的可能性 . 【答案】 越大 5. 为调查患慢性气管炎是否与吸烟有关,调查了 � 名 ‴〰 岁以上的人,调查结果如下: 患慢性气管炎 未患慢性气管炎 合计 吸烟 � ��� �〰‴不吸烟 � ��� ��合计 ‴� �� �根据列联表数据,求得 � � ‴ . 【答案】 䁣��� 6. 电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了 �〰〰 名观众进行 调查,其中女性有 ‴‴ 名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分 布直方图: 将日均收看该体育节目时间不低于 �〰 分钟的观众称为"体育迷",已知"体育迷"中有 �〰 名女性. 附: � � ‴ � ������ � ������ � ������������ � � � �� 〰䁣〰‴ 〰䁣〰� � 䁣��� �䁣�‴(1)根据已知条件完成下面的 � � � 列联表,并据此资料你是否认为"体育迷"与性别有关? 非体育迷 体育迷 合计 男 女 合计 【解】 由频率分布直方图可知,在抽取的 �〰〰 人中,"体育迷"有 �‴ 人,从而完成 � � � 列联表如下: 非体育迷 体育迷 合计 男 〰 �‴ �‴女 �‴ �〰 ‴‴合计 ‴ �‴ �〰〰 将 � � � 列联表中的数据代入公式计算,得 � � ‴ � ������ � ������ � ������������ ‴ �〰〰 � 〰 � �〰 � �‴ � �‴ � ‴ � �‴ � �‴ � ‴‴ ‴ �〰〰 � 䁣〰〰䁣因为 䁣〰〰 关 䁣��� ,所以没有理由认为"体育迷"与性别有关. (2)将日均收看该体育节目不低于 ‴〰 分钟的观众称为"超级体育迷",已知"超级体育迷"中有 � 名女性.若从"超级体育迷"中任意选取 � 人,求至少有 1 名女性观众的概率. 【解】 由频率分布直方图可知,"超级体育迷"为 ‴ 人,从而一切可能结果所组成的基本事 件空间为 � ‴ h��h� � h��h � h��h � h��l� � h��l� � h��l� � h��l� � h�l� � h�l� � l��l� � 其中 h� 表示男性, � ‴ ���� ; l� 表示女性, � ‴ ��� . � 由 �〰 个基本事件组成,而且这些基本事件的出现是等可能的. 用 � 表示"任选 � 人中,至少有 � 人是女性"这一事件,则 � ‴ h��l� � h��l� � h��l� � h��l� � h�l� � h�l� � l��l� � 事件 � 由 个基本事件组成,因而 � � ‴ �〰 䁣 7. 为研究不同的给药方式(口服或注射)和药的效果(有效与无效)是否有关,进行了相应 的抽样调查,调查结果如表所示.根据所选择的 �� 个病人的数据,能否作出药的效果与给 药方式有关的结论? � 有效 无效 合计 口服 ‴� �〰 ��注射 �� � �‴合计 ��� � �� 【解】 提出假设 �〰 :药的效果与给药方式没有关系.由列联表中的数据,算出 � � ‴ �� � ‴� � � � �〰 � �� � ��� � � � �� � �‴ � �䁣��� 关 �䁣〰��查表有 � � � ��䁣〰� ‴ 〰䁣�‴䁣 当 �〰 成立时, � � ��䁣��� 的概率大于 �‴〴 ,这个概率比较大,所以根据目前的调查数据,不 能否定假设 �〰 ,即不能作出药的效果与给药方式有关的结论. 8. 下表是一次针对高三文科学生的调查所得的数据,试问:文科学生总成绩不好与数学成绩 不好有关系吗? 总成绩好 总成绩不好 总计 数学成绩好 �� �� ��〰数学成绩不好 �� �� ��总计 � � �� 【解】 依题意,得 � � ‴ ��� ����������� � ��〰������� � �䁣� ⸲ 䁣��� . 所以在犯错误的概率不超过 〰䁣〰‴ 的前提下,认为“文科学生总成绩不好与数学成绩不好有关 系”. 9. 下表中给出了某周内中学生是否喝过酒的随机调查结果,若要使结论的可靠性不低于 �‴〴 , 根据所调查的数据,能否作出该周内中学生是否喝过酒与性别有关的结论? 喝过酒 没喝过酒 总计 男生 �〰� ���女生 �� ��� ��总计 � ‴�� ��� 【解】 提出假设 �〰 :该周内中学生是否喝过酒与性别无关. 由列联表中的数据,算出 � � � �䁣��� , 当 �〰 成立时, � � �䁣��� 的概率约为 〰䁣〰‴ ,而这里 � � � �䁣��� 关 䁣��� , 所以,不能推断出喝酒与性别有关的结论. 10. 为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了 ‴〰〰 位 老年人,结果如下: 附: � � ‴ � h݀�l� � h�l ��݀ h�� l�݀ � � � ⸲ � 〰䁣〰‴〰 〰䁣〰�〰 〰䁣〰〰� � 䁣��� �䁣�‴ �〰䁣���(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例; 【答案】 该地区老年人中需要帮助的老年人的比例为 ��〴 . 【分析】 用抽样中需要帮助的人数比抽查总数进行估计. 【解】 因为调查的 ‴〰〰 位老年人中有 �〰 � 〰 ‴ 〰 位需要志愿者提供帮助, 所以该地区老年人中需要帮助的老年人的比例的估算值为 〰 ‴〰〰 ‴ ��〴 . (2)能否有 ��〴 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关? 【答案】 有 ��〴 的把握认为该地区的老年人是否需要帮助与性别有关. 【分析】 考查独立性检验,将数据代入公式计算观测值,对照表格得出相关结论. 【解】 根据列联表所给的数据,代入随机变量的观测值公式, � � ‴ ‴〰〰 � �〰 � �〰 � 〰 � ��〰 � �〰〰 � 〰〰 � 〰 � �〰 ‴ �䁣��䁣因为 �䁣�� ⸲ �䁣�‴ ,所以有 ��〴 的把握认为该地区的老年人是否需要帮助与性别有关. (3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老 年人的比例?说明理由. 【答案】 略. 【分析】 根据样本特点给出合理建议即可. 【解】 由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看 出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地 区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比用简单随机抽样 方法更好. 课后练习 1. 已知一组数据 �� , �� , � , ��〰 的方差是 � ,且 �� � � � �� � � � � � ��〰 � � ‴ ��〰 ,则 � ‴ . 2. 某班数学测验,各分数段情况如下: 分数段 不及格 �〰��� 〰�� �〰��� �〰��〰〰 �〰〰人数 ‴ �〰 �‴ � � �若分数大于等于 �〰 分就是优良,则该班本次数学测验达到优良的频率是 . 3. 已知一组数据为 ‴〰 , �� , � , �〰 ��‴ , �� , �� ,则中位数是 . 4. 设等差数列 h� 的公差为 � ,则 h��h��h�h��h‴ 的方差 � � ‴ . 5. 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了 �‴〰 分到 �‴〰 分之 间的 �〰〰〰 名学生的成绩,并根据这 �〰〰〰 名学生的成绩画出样本的频率分布直方图(如图), 则成绩在 〰〰�‴〰 内的学生人数为 . 6. 某中学高三(1)班中选出 ‴ 名学生参加数学竞赛,他们取得的成绩(满分 �〰〰 分)的茎叶 图如图,这 ‴ 名学生成绩的众数是 �‴ ,则这组数据的方差为 . 7. 为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在 � 场比赛中的得分, 用茎叶图表示如图,则该组数据的方差为 �� . 8. 在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 , . 甲 乙 � � � � � � ‴ � ‴ � � � � � ‴ ‴ ‴ � � 9. 甲、乙两个学习小组各有 �〰 名同学,他们在一次数学测验中成绩的茎叶图如图,则他们在 这次测验中成绩较好的是 组. 10. 对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),若该样 本的中位数为 � ,众 数为 � ,则 � � � 的值为 . 11. 数据 �䁣� , �䁣� , �〰 , �〰䁣� , �〰䁣� 的平均数为 . 12. 五个数 �������h 的平均数是 ,这五个数的方差是 . 13. 一种水稻试验品种连续 ‴ 年的平均单位面积产量(单位: t/hm � )如下: �䁣� , �䁣� , �〰䁣� , �〰 , �〰䁣� ,则该组数据的方差为 . 14. 如图,茎叶图记录了甲、乙两组各 名同学在期末考试中的数学成绩,则方差较小的那组 同学成绩的方差为 . 15. 数据 h� , h� , h , � , h� 的方差为 � � ,平均数为 � ,则 (1)数据 �h� � l , �h� � l , �h � l , � , �h� � l �l � 〰 的标准差为 ,平均数 为 ; (2)数据 � h� � l , � h� � l , � h � l , � , � h� � l �l � 〰 的标准差为 ,平 均数为 . 16. 具有线性相关关系的变量 � , � ,满足一组数据如下表所示: � 〰 � � � � � � � �若 � 与 � 的回归直线方程为 �� ‴ � � � ,则 � 的值为 . 17. 已知两个具有线性相关关系的变量 � 与 � 的几组数据如下表 � � ‴ � � ‴ � � � � �根据上表数据所得线性回归直线方程为 �� ‴ �〰 � � �〰 ,则 � ‴ . 18. 调查了某地若干户家庭的年收入 � (单位:万元)和年饮食支出 � (单位:万元),调 查显示年收入 � 与年饮食支出 � 具有线性相关关系,并由调查数据得到 � 对 � 的回归直 线方程: �� ‴ 〰䁣�‴�� � 〰䁣�� .由回归直线方程可知,家庭收入每增加 � 万元,年饮食支出 平均增加 万元. 19. 下表是某厂 � � � 月份用水量(单位:百吨)的一组数据, 月份 � � � �用水量 � �䁣‴ � �䁣‴由其散点图可知,用水量 � 与月份 � 之间有较好的线性相关关系,其线性回归方程是 �� ‴� 〰䁣� � h ,则 h ‴ . 20. 独立性检验所采用的思路是:要研究 � 、 � 两类型变量彼此相关,首先假设这两类变量彼 此 ,在此假设下构造随机变量 � � ,如果 � � 的观测值较大,那么在一定程度上说明 假设 . 21. 在一次试验中,测得 ��� 的 � 组数值分别是 〰�� � ��� � �� � ��‴ ,那么 � 与 � 之间的回 归直线方程是 22. 已知两个变量 � 和 � 之间有线性相关关系, ‴ 次试验的观测数据如下: � �〰〰 ��〰 ��〰 ��〰 ��〰 � �‴ ‴� �� ‴ ��那么变量 � 对 � 的回归直线方程是 . 23. 为考虑广告费用 � 与销售额 � 之间的关系,抽取了 ‴ 家餐厅,得到如下数据: 广告费用 千元 �䁣〰 �䁣〰 �䁣〰 �〰䁣〰 ��䁣〰销售额 千元 ��䁣〰 ��䁣〰 �〰䁣〰 ‴�䁣〰 ‴䁣〰 现要使销售额达到 � 万元,则需广告费用为 .(保留两位有效数字) 24. 考古学家通过始祖鸟化石标本发现:其股骨长度 � cm 与肱骨长度 � cm 的线性回归方程 为 �� = �䁣��� - 䁣��〰 ,由此估计,当股骨长度为 ‴〰cm 时,肱骨长度的估计值为 cm . 25. 某地区恩格尔系数 � 〴 与年份 � 的统计数据如下表: 年份 � �〰〰� �〰〰‴ �〰〰� �〰〰恩格尔系数 � 〴 � �‴䁣‴ �䁣‴ ��从散点图可以看出 � 与 � 线性相关,且可得回归方程为 �� ‴ l�� � �〰‴‴䁣�‴ ,据此模型可预测 �〰�� 年该地区的恩格尔系数 〴 为 . 26. � 和 � 的散点图如图,则下列说法中所有正确命题的序号为 . ① � 、 � 是负相关关系; ②在该相关关系中,若用 � ‴ ��e ��� 拟合时的相关指数为 �� � ,用 � ‴ l� � h 拟合时的相关指 数为 �� � ,则 �� � ⸲ �� � ; ③ � 、 � 之间不能建立回归直线方程. 27. 某工厂经过技术改造后,降低了能源消耗,经统计该厂某种产品的产量 � (单位:吨)与 相应的生产能耗 � (单位:吨)有如下几组样本数据: �/ 吨 � ‴ � �/ 吨 �䁣‴ � �䁣‴根据相关检验,这组样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率 为 〰䁣 .已知该产品的年产量为 �〰 吨,则该工厂每年大约消耗的汽油为 吨. 28. 在残差分析中,残差图的纵坐标为 . 29. 由一组样本数据 ����� , ����� , � , ����� 得到回归直线方程 �� ‴ l�� � h� ,那么下面说 法中正确说法的序号是 . ① 直线 �� ‴ l�� � h� 必经过点 ��� ; ② 直线 �� ‴ l�� � h� 至少经过点 ����� , ����� , � , ����� 中的一个点; ③ 直线 �� ‴ l�� � h� 的斜率为 l� ‴ �‴� � ��� ������ �‴� � �� � � ��� � ; ④ 直线 �� ‴ l�� � h� 和各点 ����� , ����� , � , ����� 的偏差 �‴� � �� � l�� � h � � 是该坐 标平面上所有直线与这些点的偏差中最小的直线. 30. 若一组观测值 ����� , ����� , � , ����� 之间满足 �� ‴ l�� � h � � � ‴ ������� .若 �恒为 〰 ,则 � � 为 . 31. 我们常利用随机变量 � � 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两 个分类变量的独立性试验,其思想类似于数学上的 . 32. 2008 年北京奥运会期间,北京某五星级宾馆上调了住宿价格.为了调查上调价格与客人所 处地区是否有关系,奥运会后,统计本国客人与外国客人的人数,与去年同期相比,结果如下: 本国客人 外国客人 合计 �〰〰 年 ��� �� �‴� �〰〰� 年 �� ‴� �合计 �� ‴�� �通过计算,可得统计量 � � ‴ ,我们可以得到结论: . 33. 调查了 ‴�〰 名中年人,其中 �� 人有高血压史,其他 �� 人无高血压史.有高血压史的 �� 人中有 �� 人有冠心病,在无高血压史的 �� 人中有 � 人有冠心病.根据上述数据分析, 我们得出 � � ‴ . 34. 对过度看电视与近视之间关系的一项调查,根据样本数据计算得 � � 的值大于 䁣��� ,则我 们至少有 的把握认为过度看电视与近视有关. 35. 考察棉花种子经过处理跟生病之间的关系得到如下表所示的数据: 种子处理 种子未处理 合计 得病 � �〰� �不得病 �� �� ��合计 � �� �〰根据以上数据,则统计量 � � 的值是 . 36. 对某校高二年级学生参加社区服务次数进行统计,随机抽取 � 名学生作为样本,得到这 �名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: 分组 频数 频率 �� �〰 � ��� � � ���� � � ����‴ � 〰䁣〰‴ 合计 � � (1)求出表中 � , � 及图中 h 的值; (2)在所取样本中,从参加社区服务的次数不少于 � 次的学生中任选 � 人,求至少有一人参 加社区服务次数在区间 ����‴ 内的概率. 37. 某地区为了了解当地高中生的身体发育情况,对某一中学随机抽取的 ‴〰 名学生的体重进行 了测量,结果如下:(单位: kg ) �� , � , �� , � , �� , � , ‴� , � , � , �� , �〰 , ‴� , � , �� , �� , ‴〰 , , �� , �‴ , �� , � , �‴ , ‴ , �� , , �� , �� , ‴〰 , , �� , �� , � , ‴� , ‴� , � , � , ‴� , �� , �‴ , � , ‴ , �� , �‴ , � , ‴� , � , ‴� , � , �� , ‴� . (1)若以组距为 ‴ ,完成下面样本频率分布表; 分组 频数 频率 频率 / 组距 ��� 〰䁣〰� �� 〰䁣〰� ��� � ���� 〰䁣〰�� ��‴� ‴��‴ ‴ ‴��� � ���� 〰䁣〰� 合计 ‴〰 �䁣〰〰(2)根据(1)中的频率分布表,画出频率分布直方图; (3)若本地区学生总人数为 〰〰〰 人,试根据抽样比例估计本地区学生体重在区间 �‴ 内 所占的人数约为多少人? 38. 从某校高一的 �〰〰� 名学生中用系统抽样的方法抽取一个容量为 �〰〰 的身高样本,数据如 下(单位: cm ),试作出该样本的频率分布表. �� ��‴ �� �� �〰 ��‴ �〰 �‴� �‴ ��� �‴� �〰 ��� ��� �� ��� ��� �‴‴ ��� ��‴ ��� �‴‴ ��� �‴� �‴‴ ��〰 ��〰 ��� �‴� �〰 �� �〰 ��� ��� �� �� ��‴ �� �� ��〰 ��� �� � �‴� �� �� �� ��〰 ��� ��〰 ��� ��� �‴� ��� �� �‴‴ ��‴ ��‴ ��� �‴� �� �‴� �‴ ��‴ ��� �‴� �� ��� �� � �‴‴ ��‴ �‴� �〰 ��� �‴� �‴‴ �� �‴ �� ��� �� ��� �‴� ��� �� ��� ��� �� �� ��� ��‴ �� �‴� �� ��� ��� ��� ��� ��� 39. 班有 �〰 名学生,在某次数学单元测验中的成绩如下表所示: 成绩 分 ‴ � � � �� � �� �� ��人数 � � � � � � � �求总体平均数和总体中位数、方差和标准差. 40. 在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有 �〰〰 个数据,将数据 分组如下表: 分组 频数 �䁣〰��䁣� � �䁣���䁣� �‴ �䁣���䁣�� 〰 �䁣����䁣�� �� �䁣����䁣‴〰 �〰 �䁣‴〰��䁣‴� � 合计 �〰〰(1)完成频率分布表,并在坐标系中画出频率分布直方图; 分组 频数 频率 �䁣〰��䁣� � �䁣���䁣� �‴ �䁣���䁣�� 〰 �䁣����䁣�� �� �䁣����䁣‴〰 �〰 �䁣‴〰��䁣‴� � 合计 (2)估计纤度落在 �䁣���䁣‴〰 中的概率及纤度小于 �䁣�〰 的概率.(用落在区间内的频率表示 落在该区间的概率) 41. 某良种培育基地正在培育一种小麦新品种 � .将其与原有的一个优良品种 � 进行对照试 验.两种小麦各种植了 �‴ 亩,所得亩产数据(单位: kg )如下: 品种 � : ‴ , ‴� , � , �� , ‴ , �� , �� , �� , �〰〰 , �〰‴ , ��� , ��� , ��‴ , ��� , �� , �� , �� , �〰 , �〰 , �� , �� , ��‴ , ��‴ , �‴� , �‴�品种 � : � , � , � , � , �‴ , �� , �� , �� , �� , �� , �‴ , � , � , �〰〰 , �〰� , �〰� , �〰 , �〰� , �〰 , ��〰 , ��� , ��‴ , ��� , ��� , �〰(1)完成数据的茎叶图; (2)用茎叶图处理现有的数据,有什么优点? (3)通过观察茎叶图,对品种 � 与 � 的亩产量及其稳定性进行比较,写出统计结论. 42. 某车间共有 ��〰 名工人,随机抽取 � 名,他们某日加工零件个数的茎叶图如图所示,其中 茎为十位数,叶为个位数. (1)计算样本的平均数,并估计该车间 ��〰 名工人的日加工零件个数; (2)日加工零件个数大于样本的平均数的工人为优秀工人,根据茎叶图推断该车间 ��〰 名工 人中有几名优秀工人. 43. 下面是甲、乙两个俱乐部,某赛季一些场次得分的茎叶图(如图): 甲 乙 〰 � ‴ 〰 � � � � � � � � � ‴ � � � � � � � � � ‴ �(1)甲、乙两个俱乐部的最高分各是多少? (2)哪一个俱乐部成绩好一些? 44. 甲、乙两小组各 �〰 名学生的英语口语测试成绩如下(单位:分): 甲组 � � �〰 �� �� �� � �� �� �‴ �乙组 � �� �� �‴ �� � �〰 �� �� � �用茎叶图表示两个小组的成绩,并判断哪个小组的成绩更整齐一些. 45. 为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各 抽取 〰 名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图: 甲 乙 � ‴ ‴ � ‴ � ‴ ‴ � � 〰 〰 � 〰 � � � � � � ‴ � � � � � � � 〰 〰 〰 〰 � � � � � � ‴ � � � � � � ‴ ‴ � � 〰 � 〰(1)若甲校高三年级每位学生被抽取的概率为 〰䁣〰‴ ,求甲校高三年级学生总人数,并估计甲 校高三年级这次联考数学成绩的及格率( �〰 分及 �〰 分以上为及格); (2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为 ����� ,估计 �� � �� 的值. 46. 汽车行业是碳排放量比较大的行业之一,欧盟规定,从 2012 年开始,对 ��� 排放量超过 �〰��g/km 的 MI 型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类 MI 型品牌 的新车各抽取了 ‴ 辆进行 ��� 排放量检测,记录如下(单位: g/km ): 甲 �〰 ��〰 ��〰 ��〰 �‴〰乙 �〰〰 ��〰 � � ��〰经测算发现,乙类品牌车 ��� 排放量的均值为 � 乙 ‴ ��〰�g/km . (1)求甲类品牌汽车的排放量的平均值及方差; (2)若乙类品牌汽车比甲类品牌汽车 ��� 的排放量稳定性好,求 � 的取值范围. 47. 有甲、乙两个球队,甲队有 � 名队员,乙队有 �〰 名队员,他们的身高数据如下:(单位: cm ) 甲队 � �� ��� �‴ ��‴ � ��乙队 � ��〰 �� ��� ��� �� �� �� �� �� ��� � � �� ��〰 � ��� � �� � ��(1)求两队队员的平均身高; (2)比较甲、乙两队哪一队身高更整齐一些? 48. 已知一组数 � � , � � , � , � , � 其中 � 是小于 �〰 的非负整数,且数据的方差是整数,求 这组数据的标准差. 49. 某空调专卖店试销 A 、 B 、 C 三种新型空调,销售情况如下表所示: 第一周 第二周 第三周 第四周 第五周 � 型数量 台 �� �〰 �‴ �� �‴ � 型数量 台 � �� � �� �‴ � 型数量 台 �‴ � �� �� �‴ (1)求 A 型空调前三周的平均周 销售量; (2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台, 求抽到的空调不是 B 型且不是第一周售出空调的概率; (3)根据 C 型空调前三周的销售情况,预估 C 型空调五周的平均周销售量为 �〰 台,当 C 型空 调周销售量的方差最小时,求 �� , �‴ 的值.(注:方差 � � ‴ � � �� � � � � �� � � � � � �� � � � ,其中 � 为 �� , �� , � , �� 的平均数) 50. 甲、乙两台机床同时生产一种零件, �〰 天中两台机床每天出的次品数分别是 甲: 〰 � 〰 � � 〰 � � �乙: � � � 〰 � � � 〰 �分别计算这两组数据的平均数与方差,从计算结果看哪台机床的性能比较好? 51. 某种产品的广告费用支出 � 与 销售额 � (单位:百万元)之间,有如下对应数据: � � � ‴ � � � 〰 �〰 �〰 ‴〰 〰 (1)请画出自变量 � 与因变量 � 的散点图; (2)对 ��� 进行回归分析,如果 ��� 之间存在线性回归关系,则求出回归直线方程; (3)试预测广告支出为 �〰 百万元时,销售额应该多大? 52. 某产品的广告费用支出 � 与销售额 � (单位:百万元)之间有如下的对应数据: �/ 百万元 � � ‴ � � �/ 百万元 〰 �〰 �〰 ‴〰 〰附:参考数据: � � � � � � ‴ � � � � � � � ‴ ��‴ , � � 〰 � � � �〰 � ‴ � �〰 � � � ‴〰 � � � 〰 ‴ ��〰 . 参考公式:回归直线的方程 �� ‴ l�� � h� ,其中 l� ‴ �‴� � ����� ���� �‴� � ���� � � ‴ �‴� � ����� ���� �‴� � �� � � ��� � , h� ‴ � � l�� , � , � 为样本平均值. (1)求 � 与 � 之间的回归直线方程; (2)试预测广告费用支出为 � 千万元时,销售额是多少? 53. 为了比较注射 A , B 两种药物后产生的皮肤疤疹的面积,选 �〰〰 只家兔做试验,将这 �〰〰只家兔随机地分成两组.每组 �〰〰 只,其中一组注射药物 A ,另一组注射药物 B .下表 � 和表 � 分别是注射药物 A 和药物 B 后的试验结果.(疤疹面积单位: mm � ) 表 � :注射药物 A 后皮肤疱疹面积得频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰频数 〰 �〰 �〰 �〰表 � :注射药物 B 后皮肤疱疹面积得频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰 �〰��‴频数 �〰 �‴ �〰 〰 �‴ (1)完成下面的频率分布直方图, 并比较注射两种药物后疤疹面积的中位数大小; 如图 注射药物 A 后皮肤疱疹面积的频率分布直方图 如图 注射药物 B 后皮肤疱疹面积的频率分布直方图 (2)完成下面的列联表,并回答能否有 ��䁣�〴 的把握认为“注射药物 A 后的疤疹面积与注射药 物 B 后的疤疹面积有差异”. 疱疹面积小于 〰�mm � 疱疹面积不小于 〰�mm � 合计 注射药物 A h ‴ l ‴注射药物 B � ‴ ݀ ‴合计 � ‴附: � � ‴ � h݀�l� � h�l ��݀ h�� l�݀ . � � � �� 〰䁣�〰〰 〰䁣〰‴〰 〰䁣〰�‴ 〰䁣〰�〰 〰䁣〰〰� � �䁣〰� 䁣��� ‴䁣〰�� �䁣�‴ �〰䁣���54. 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能 耗(吨标准煤)的几组对照数据. � � ‴ � � �䁣‴ � �䁣‴ (1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出关于 的线性回归方程 � ‴ l�� � h� ; (3)已知该厂技改前 �〰〰 吨甲产品的生产能耗为 �〰 吨标准煤.试根据(2)求出的线性回归 方程,预测生产 �〰〰 吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值: � �䁣‴ � � � � ‴ � � � � � �䁣‴ ‴ ��䁣‴ ) (用最小二乘法求线性回归方程系数公式 l� ‴ �‴� � ��������� �‴� � �� � ��� � � , h� ‴ � � l�� ) 55. 为了研究男子的年龄与吸烟的关系,抽查了 �〰〰 位男性,按年龄超过和不超过 �〰 岁,吸 烟量每天多于和不多于 �〰 支进行分组.如下表: 试问吸烟量与年龄是否有关? 56. 某种产品的广告费支出 � 与销售额 � 之间有如下对应数据(单位:百万元) � � � ‴ � � � 〰 �〰 �〰 ‴〰 〰(1)画出散点图; (2)从散点图中判断销售金额与广告费支出成什么样的关系? 57. 为了研究高中女生身高与体重的关系,从某高中随机选取 � 名女生,测量其身高与体重的 数据,具体如下表: 编号 � � � ‴ � �身高 /cm �‴‴ �‴ ��‴ ��‴ ��‴ �〰 �〰 �‴体重 /kg � ‴〰 �� ‴ �� ‴� ‴� ��(1)请根据上表提供的数据,求出体重 � 关于身高 � 的线性回归方程; (2)试根据(1)的回归方程,预计一名身高 ��〰�cm 的女高中生的体重. 58. 一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损 的统计数据如下表所示: 转速 � 转 / 秒 �� �� �� �每小时生产有缺损零件数 � 个 �� � � ‴(1)作出散点图; (2)如果 � 与 � 线性相关,求出回归直线方程; (3)若实际生产中,允许每小时的产品中有缺损的零件最多为 �〰 个,那么,机器的运转速度 应控制在什么范围内? 59. 下面是一周内某地申请领取结婚证的新郎与新娘的年龄,记录(新郎年龄,新娘年龄)如 下: �〰 , 〰�� , �‴�‴� , �‴��〰 , ��〰 , ����� , �‴�� , ����� , ���� , ����‴ , ����� , �� , ���� , ����� , �� . (1)对于上面的实际年龄统计数据求出线性回归方程; (2)从这条回归直线上,你对新娘和新郎的年龄模型可得出什么结论? 60. 某品牌服装的广告费支出 � (单位:万元)与销售额 � (单位:万元)之间有如下的对应数 据: 广告费 � � � � � �〰销售额 � �� �� �〰‴ ��‴ �〰试画出散点图,并判断广告费 � 与销售额 � 是否线性相关? 61. 某种产品的广告费支出 � 与销售额 � (单位:万元)之间有如下对应数据: � � � ‴ � � � 〰 �〰 �〰 ‴〰 〰若广告费支出 � 与销售额 � 回归直线方程为 �� ‴ �䁣‴� � h h � R . (1)试预测当广告费支出为 �� 万元时,销售额是多少? (2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值 不超过 ‴ 的概率. 62. 某工业部门进行一项研究,分析该部门的年产量与生产费用的样本,从这个工业部门内随 机抽选了 �〰 个企业作样本,有如下资料: 年产量 千件 � �〰 �� �� ‴‴ �‴ � �� �〰〰 ��〰 ��〰生产费用 千元 � �‴〰 ��〰 ��〰 �〰 �‴〰 ��� ��‴ ��‴ ��〰 ��‴(1)画出散点图; (2)对这两个变量之间是否存在线性相关进行相关性检验; (3)该部门欲建一个年产量为 �〰〰 千件的企业,预测其生产费用. 63. 下图是我国 �〰〰� 年至 �〰�� 年生活垃圾无害化处理量(单位:亿吨)的折线图. 附注: 参考数据: �‴� ��� ‴ �䁣� , �‴� ��� �� ‴ �〰䁣� , �‴� �� � � � � ‴ 〰䁣‴‴ , � �䁣��� . 参考公式:相关系数 � ‴ �‴� � ����� ���� �‴� � ���� � � �‴� � ���� � �回归方程 �� ‴ h� � l�� 中斜率和截距的最小二乘估计公式分别为: l� ‴ �‴� � ����� ���� �‴� � ���� � � , h� ‴ � � l�� . (1)由折线图看出,可用线性回归模型拟合 � 与 � 的关系,请用相关系数加以说明; (2)建立 � 关于 � 的回归方程(系数精确到 〰䁣〰� ),预测 �〰�� 年我国生活垃圾无害化处理量. 64. 检查 ‴ 位同学统计学的学习时间与成绩分数如下表: 每周学习时间 � � �〰 �学习成绩 �〰 �〰 ‴〰 〰 �〰 试求: (1)学习时间与学习成绩之间的相关系数; (2)成绩对学习时间的直线回归方程. 65. 某种产品的产量与单位成本的资料如下: 产量 � 千件 � � � ‴单位成本 � 元 / 件 � � �� �� 试求: (1)计算相关系数 � ; (2) � 对 � 的线性回归方程; (3)指出产量每增加 �〰〰〰 件时,单位成本平均下降了多少元? 参考公式: �� ‴ �‴� � �� � ��� �� � �� �‴� � �� � �� � � ‴ �‴� � ����� � � � ��� �‴� � �� � � � �� � � � � ‴� � �� � � ��� � ‴ �‴� � �� � ��� �� � �� �‴� � �� � �� � � �‴� � �� � �� � � ‴ �‴� � ����� � � � ��� �‴� � �� � � � �� � � �‴� � �� � � � �� � � 66. 某企业有两个分厂生产某种零件,按规定内径尺寸(单位: mm )的值落在 ��䁣���〰䁣〰�的零件为优质品.从两个分厂生产的零件中各抽出了 ‴〰〰 件,量其内径尺寸,得结果如下表. 甲厂: 分组 ��䁣�����䁣�〰 ��䁣�〰���䁣�� ��䁣�����䁣��频数 �� � ��分组 ��䁣���〰䁣〰� 〰䁣〰��〰䁣〰� 〰䁣〰��〰䁣�〰频数 ��� �� ��分组 〰䁣�〰�〰䁣��频数 �乙厂: 分组 ��䁣�����䁣�〰 ��䁣�〰���䁣�� ��䁣�����䁣��频数 �� � �‴分组 ��䁣���〰䁣〰� 〰䁣〰��〰䁣〰� 〰䁣〰��〰䁣�〰频数 �‴� � ��分组 〰䁣�〰�〰䁣��频数 ��(1)试分别估计两个分厂生产零件的优质品率; (2)由以上统计数据填下面 � � � 列联表,并问是否有 ��〴 的把握认为“两个分厂生产的零件 的质量有差异”. 甲厂 乙厂 合计 优质品 非优质品 合计 67. 气管炎是一种常见的呼吸道疾病,医药研究人员对两种中草药治疗慢性气管炎的疗效进行 对比,所得数据如表所示.问它们的疗效有无差异(可靠性不低于 ��〴 )? 有效 无效 合计 复方江剪刀草 ��� �� ��‴胆黄片 �� � �〰〰合计 �‴ 〰 �‴ 68. 某大型科研中心为了研究科研人员工作积极性和对待科研改革态度的关系,随机抽取了 ��� 名科研人员进行调查,所得数据如下表所示: 积极支持科研改革 不支持科研改革 总计 工作积极 ‴� �〰 ��工作一般 � � �‴总计 �� �〰 ���对于科研中心的科研改革项目,根据上述数据能得出什么结论? 69. 1972 年调查某桑场采桑人员和不采桑人员的桑毛虫皮炎发病情况,结果如下表所示,利用 列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系犯错误的概率是 多少? 采桑 不采桑 合计 患者人数 �� �� 〰健康人数 ‴ � �合计 � �〰 �� 70. 从发生汽车碰撞事故的司机中抽取 �〰〰〰 名司机.根据他们的血液中含有酒精以及他们是 否对事故负有责任,将数据整理如下: 那么,司机对事故负有责任与血液中含有酒精是否有关系?若有关系,你认为在多大程度上有 关系? 统计-出门考 姓名 成绩 1. 某人将一枚硬币抛了 �〰 次,正面朝上出现了 �� 次,则事件“正面朝上”出现的频数 是 ,频率是 . 2. 已知五名运动员中四名运动员的得分分别是 � , � , � , � ,还有一名运动员 � 的得分不知道, 若五人得分的标准差为 � ,则运动员 � 的得分是 . 3. �〰 名工人某天生产同—零件,生产的件数是 �‴ , � , �� , �〰 , �‴ , � , � , �� , �� , �� , 设其平均数为 h ,中位数为 l ,众数为 � ,则有 . 4. 如图是甲、乙两名同学进入高中以来 ‴ 次体育测试成绩(单位:分)的茎叶图,则甲 ‴ 次 测试成绩的平均数是 ,乙 ‴ 次测试成绩的平均数与中位数之差是 . 5. 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示,则该赛季发挥更稳 定的运动员是 .(填“甲”或“乙”) 6. 甲乙两名运动员在 � 场篮球比赛中得分的数据统计如图所示,则甲乙两人发挥较为稳定的 是 . 甲 乙 � 〰 � � ‴ � � ‴ � � � � � �7. 某学校高一年级男生人数占该年级学生人数的 �〰〴 .在一次考试中,男、女生平均分数分 别为 ‴ 、 �〰 ,则这次考试该年级学生平均分数为 . 8. 一种水稻试验品连续 ‴ 年的平均单位面积产量(单位:(mathrm t diagup mathrm h mathrm m^2))如下: �䁣� , �䁣� , �〰䁣� , �〰 , �〰䁣� ,则该组数据的方差为 . 9. 一个样本 h , , ‴ , 的平均数是 l ,且 h , l 是方程 � � � ‴� � � ‴ 〰 的两根,则这个样本 的方差是 . 10. 工厂生产某种产品的产量 � (吨)与相应的生产能耗 � (吨标准煤)有如下几组样本数据: � � ‴ � � �䁣‴ � �䁣‴根据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜 率为 〰䁣 ,则这组样本数据的回归直线方程是 . 11. 在一次试验中,测得 ��� 的五组值分别是 � 〰���䁣 , � �〰��䁣〰 , � �〰��‴䁣〰 � ‴〰����䁣 , � 〰���� ,则线性回归方程为 . 12. 已知回归方程 �� ‴ �䁣�� � ��䁣�� ,则可估计 � 与 � 的增长速度之比约为 . 13. 为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月 � 号 到 ‴ 号每天打篮球时间 � (单位:小时)与当天投篮命中率 � 之间的关系: 时间 �� � � � ‴命中率 �� 〰䁣� 〰䁣‴ 〰䁣� 〰䁣� 〰䁣�小李这 ‴ 天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月 � 号打 �小时篮球的投篮命中率为 . 14. 对于回归方程 �� ‴ 䁣�‴� � �䁣〰� ,当 � ‴ �〰 时, � 的估计值是 . 15. 已知某回归直线过点 〰�〰 ,且样本数据中 �� 和 �� � ‴ ������� 的均值分别为 �䁣‴ 和 ,则 此回归直线的方程为 . 16. 某数学老师身高 ���cm ,他爷爷、父亲和儿子的身高分别是 ��cm , �〰�cm 和 ����cm .因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高 为 cm . (线性回归方程 �� ‴ l�� � h� 中系数计算公式: l� ‴ �‴� � ���� ����� �‴� � ���� � � , h� ‴ � � l�� ,其中 � , � 表示 样本均值) 17. � � 衡量回归方程的预报精度时, � � 越小,预报精度 . 18. 某工厂的设备使用年限 � (年)与维修费用 � (万元)之间的回归直线方程为 �� ‴ 〰䁣�� � �䁣‴ ,那么设备使用前 年的总维修费用约为 万元. 19. 在 ��� 分类变量 � 与 � 有关的情况下, � � ‴ �䁣� ,则 � � � �� ‴ ;此时说" � 与 � 有关"的可信度为 %. 20. 下面是 � � � 列联表: �� �� 合计 �� h �� ‴ �� �� � �‴合计 l �� �〰则表中 h ‴ , l ‴ . 21. 由 � � � 列联表中算得 � � 越大,则认为两变量有关的把握越 (填"大"或"小"). 22. 为了调查甲、乙两个交通站的车流量,随机选取了 �� 天,统计每天上午 8:00-12:00 间 各自的车流量(单位:百辆),得如下所示的统计图, (1)甲、乙两个交通站的车流量的极差分别是多少? (2)甲交通站的车流量在间的频率是多少? (3)甲、乙两个交通站哪个站更繁忙?并说明理由. 23. 有 �〰 个数据,它们的标准差是 䁣‴ ,且各数与 �〰 的差的平方和为 �‴〰〰 ,求这 �〰 个数据 的平均值. 24. 三(1)班的 �〰 名学生在数学期中考试中的成绩如下(考分): �� , �� , �〰 , , , � , �� , � , �� , ‴� 求这 �〰 个数的总体平均数、总体中位数、总体方差和标准差. 25. 为了了解甲、乙两名同学的数学学习情况,对他们的 次数学测试成绩(满分 �〰〰 分)进 行统计,作出如下的茎叶图,其中 � , � 处的数字模糊不清.已知甲同学成绩的中位数是 � , 乙同学成绩的平均分是 �� 分. 甲 乙 � � � � � � � � 〰 � �(1)求 � 和 � 的值; (2)现从成绩在 �〰��〰〰 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的 概率. 26. 随机抽取某中学甲、乙两班各 �〰 名同学,测量他们的身高(单位: cm )获得身高数据的 茎叶图如图(中间的数字表示身高的百位数字、十位数字,旁边的数字分别表示身高的个位数 字). (1)根据茎叶图判断哪个班的平均身高较高; (2)计算甲班的样本方差. 27. 甲、乙两个小组各 �〰 名学生的英语口语测试成绩(单位:分)如下: 甲组: � �〰 �� �� �� � �� �� �‴ �乙组: �� �� � �� � �〰 �� �� � �用茎叶图表示这两个小组的成绩,并判断哪个小组的成绩更整齐一些. 28. 某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进 行田间试验.选取两大块地,每大块地分成 � 小块地,在总共 �� 小块地中,随机选 � 小块地 种植品种甲,另外 � 小块地种植品种乙. 附:样本数据 ���������� 的样本方差 � � ‴ � � �� � � � � �� � � � � � � �� � � � ,其中 � 为 样本平均数. (1)假设 � ‴ � ,求第一大块地都种植品种甲的概率; (2)试验时每大块地分成 � 小块,即 � ‴ � ,试验结束后得到品种甲和品种乙在各小块地上的 每公顷产量(单位: kg/hm � )如下表: 品种甲 �〰 � �〰 �〰� �� �〰〰 ��� �〰�品种乙 ��� �〰 ��� ��� �〰� �� �〰〰 ��分别求品种甲和品种乙每公顷产量的样本平均数和样本方差;根据试验结果,你应该种植哪 一品种? 29. 某工厂人员及工资构成如表: 人员 经理 管理人员 高级技工 技工 学徒 合计 周工资 ��〰〰 �‴〰 ��〰 �〰〰 �〰〰 ��〰人数 � � ‴ �〰 � �合计 ��〰〰 �‴〰〰 ��〰〰 �〰〰〰 �〰〰 �〰〰〰(1)指出这个问题中工资的众数、中位数、平均数; (2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么? 30. 已知样本 h� , h� , � , h�� 的平均数是 h ,方差是 � � ‴ 〰䁣�〰 ,求样本 h� , h� , � , h�� , h的方差 ��� . 31. 某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得 到如下数据: 单价 � 元 � �䁣� �䁣� �䁣� �䁣� �销量 � 件 �〰 �� � �〰 ‴ ��(1)求回归直线方程 �� ‴ l� � h ,其中 l ‴� �〰�h ‴ � � l� ; (2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是 � 元/件, 为使工厂获得最大利润,该产品的单价应定为多少元?(利润 ‴ 销售收入 � 成本) 32. 为了比较注射 A , B 两种药物后产生的皮肤疱疹的面积,选 �〰〰 只家兔做试验,将这 �〰〰 只家兔随机地分成两组,每组 �〰〰 只,其中一组注射药物 A,另一组注射药物 B. 附: � � ‴ � h݀�l� � h�l ��݀ h�� l�݀ � � � �� 〰䁣�〰〰 〰䁣〰‴〰 〰䁣〰�‴ 〰䁣〰�〰 〰䁣〰〰� � �䁣〰� 䁣��� ‴䁣〰�� �䁣�‴ �〰䁣���(1)甲、乙是 �〰〰 只家兔中的 � 只,求甲、乙分在不同组的概率; (2)下表 1 和表 2 分别是注射药物 A 和 B 后的试验结果.(疱疹面积单位: mm � ) 表 1:注射药物 A 后皮肤疱疹面积的频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰频数 〰 �〰 �〰 �〰表 2:注射药物 B 后皮肤疱疹面积的频数分布表 疱疹面积 �〰��‴ �‴�〰 〰�‴ ‴��〰 �〰��‴频数 �〰 �‴ �〰 〰 �‴ (i)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小; (ii)完成下面 � � � 列联表,并回答能否有 ��䁣�〴 的把握认为“注射药物 A 后的疱疹面积与 注射药物 B 后的疱疹面积有差异”. 表 3: 疱疹面积小于 �〰�mm � 疱疹面积不小于 �〰�mm � 合计 注射药物 �A h ‴ l ‴注射药物 �B � ‴ ݀ ‴合计 � ‴ 33. 某连锁经营公司所属的 ‴ 个零售店某月的销售额和利润额资料如下表: 商店名称 � � � � �销售额 � / 千万元 ‴ � �利润额 � / 百万元 � � ‴(1)画出销售额和利润额的散点图,并判断销售额和利润额是否具有相关关系; (2)求利润额 � 对销售额 � 的回归直线方程. 34. 某地最近十年粮食需求量逐年上升,下表是部分统计数据: 年份 �〰〰� �〰〰� �〰〰� �〰〰� �〰�〰需求量 万吨 �� ��� �‴ �� ���(1)利用所给数据求年需求量与年份之间的回归直线方程 �� ‴ l� � h ; (2)利用(1)中所求出的直线方程预测该地 �〰�� 年的粮食需求量. 35. PM�䁣‴ 是指空气中直径小于或等于 �䁣‴ 微米的颗粒物(也称可入肺颗粒物).为了探究车 流量与 PM�䁣‴ 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与 PM�䁣‴ 的数 据如下表: 时间 周一 周二 周三 周四 周五 车流量 �� 万辆 ‴〰 ‴� ‴� ‴ ‴� PM�䁣‴� 的浓度 �� 微克 / 立方米 �� 〰 � � �(1)根据上表数据,请在下列坐标系中画出散点图; (2)根据上表数据,用最小二乘法求出 � 关于 � 的线性回归方程 �� ‴ l�� � h� ; (3)若周六同一时间段的车流量是 �‴ 万辆,试根据(2)求出的线性回归方程预测,此时 PM�䁣‴ 的浓度为多少(保留整数)? 36. 某地高校教育经费 � 与高校学生人数 � 连续 � 年的统计资料如下: 教育经费 � 万元 �� � � ��� �‴‴学生人数 � 万人 �� �� �� �〰 �� �‴试求回归直线方程,估计教育经费为 ‴〰〰 万元时的在校学生数. 37. 某种产品的产量与单位成本的资料如下: 产量 千件 � � � ‴单位成本 元 / 件 � � �� �� 试求: (1)计算相关系数 � ; (2) � 对 � 直线回归方程; (3)指出产量每增加 �〰〰〰 件时,单位成本平均下降了多少元? 38. 在 ‴ 块田地上进行小麦的对比试验,在同样的施肥量和管理水平下,给出了小麦的基本苗 数 � 和成熟小麦的有效穗数 � 的数据如下表.计算 � 与 � 的相关系数. 基本苗数 � 万株 / 亩 �‴ �‴䁣‴ 〰䁣〰 �䁣� ��䁣�有效穗数 � 万株 / 亩 �䁣� ��䁣� ��䁣〰 �䁣� ��䁣� 39. 某中学部分退休教师为迎接 2008 年奥运会自发组织在一起手工制作“奥运葫芦”(将奥运会 会标"中国印 � 舞动的北京"彩绘在葫芦上),在 �〰 次制作中测得的数据如下: 奥运葫芦数 � 个 �〰 �〰 〰 �〰 ‴〰 �〰 〰 �〰 �〰 �〰〰加工时间 �/h �� �� ‴ �� �� �‴ �〰� �〰� ��‴ ���试问: (1) � 与 � 是否具有线性相关关系? (2)如果 � 与 � 具有线性相关关系,求出回归直线方程,并根据回归直线方程,预测加工 �〰〰� 个“奥运葫芦”需多少天(精确到 � 天)? 注:每天工作 � 小时. 参考公式:相关系数 相关系数( � ‴ �‴� � ��������� �‴� � �� � ��� � � �‴� � �� � ��� � � 回归直线方程是 �� ‴ l�� � h� ,其 中 l� ‴ �‴� � ��������� �‴� � �� � � ��� � �h� ‴ � � l��䁣 ) 40. 某医院分别用化学疗法和化疗结合放射两种方法治疗某种癌症患者,如表: 组别 有效 无效 合计 化疗组 �� �� �化疗加放疗组 � �〰 ��合计 ‴ � �问两种疗法有无差别? 41. 为考察某种药物预防疾病的效果,进行动物试验,得到如下的列联表: 患病 未患病 合计 服用药 �〰 �‴ ‴‴没有服用药 �〰 〰 ‴〰合计 〰 ‴ �〰‴试用三维柱形图分析服用药和患病之间是否有关系. 42. 生物学习小组在研究性别与色盲关系时,得到如下列联表: 色盲 非色盲 合计 男 �� �� �〰〰女 ‴ ��‴ �〰〰〰合计 � �� ��〰〰试判断性别与色盲是否有关系? (附: � � ‴ � ������������� � ������������ , � � � �� 〰䁣〰‴ 〰䁣〰� � 䁣��� �䁣�‴ )查看更多