- 2021-06-09 发布 |
- 37.5 KB |
- 24页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考文科数学复习备课课件:第二节 一元二次不等式及其解法
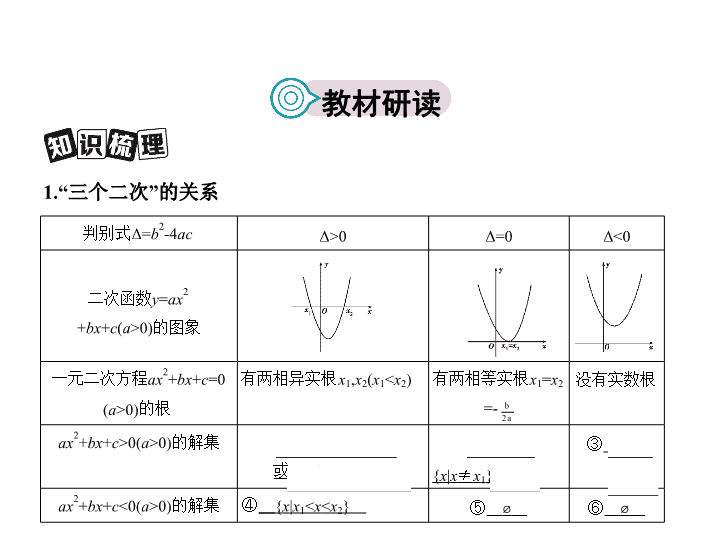
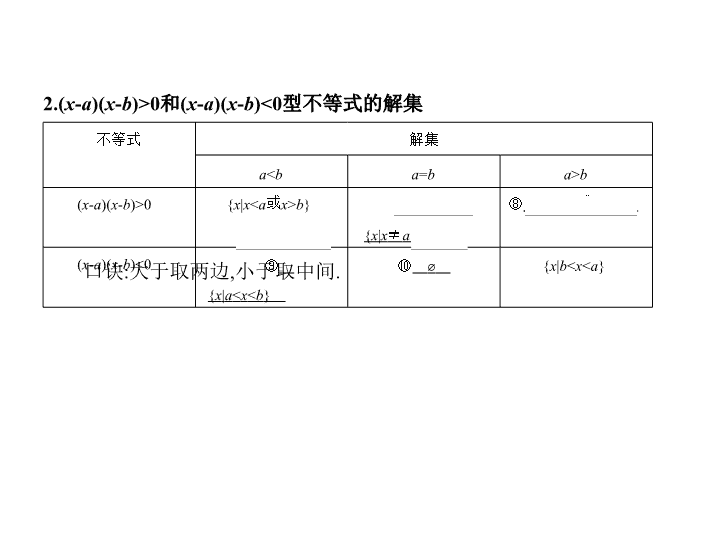
文数 课标 版 第二节 一元二次不等式及其解法 1.“三个二次”的关系 教材研读 判别式 Δ = b 2 -4 ac Δ >0 Δ =0 Δ <0 二次函数 y = ax 2 + bx + c ( a >0)的图象 一元二次方程 ax 2 + bx + c =0 ( a >0)的根 有两相异实根 x 1 , x 2 ( x 1 < x 2 ) 有两相等实根 x 1 = x 2 =- 没有实数根 ax 2 + bx + c >0( a >0)的解集 ① { x | x < x 1 或 x > x 2 } ② { x | x ≠ x 1 } ③ R ax 2 + bx + c <0( a >0)的解集 ④ { x | x 1 < x < x 2 } ⑤ ⌀ ⑥ ⌀ 2.( x - a )( x - b )>0和( x - a )( x - b )<0型不等式的解集 口诀:大于取两边,小于取中间. 不等式 解集 a < b a = b a > b ( x - a )( x - b )>0 { x | x < a 或 x > b } ⑦ { x | x ≠ a } ⑧ { x | x < b 或 x > a } ( x - a )( x - b )<0 ⑨ { x | a < x < b } ⑩ ⌀ { x | b < x < a } 判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)若不等式 ax 2 + bx + c <0的解集为( x 1 , x 2 ),则必有 a >0. (√) (2)不等式 ≤ 0与( x +2)( x -1) ≤ 0的解集相同. ( × ) (3)若不等式 ax 2 + bx + c >0的解集是(- ∞ , x 1 ) ∪ ( x 2 ,+ ∞ ),则方程 ax 2 + bx + c =0的 两个根是 x 1 和 x 2 . (√) (4)若方程 ax 2 + bx + c =0( a ≠ 0)没有实数根,则不等式 ax 2 + bx + c >0的解集 为R. ( × ) (5)一元二次不等式 ax 2 + bx + c ≤ 0在R上恒成立的条件是 a <0且 Δ = b 2 -4 ac ≤ 0. (√) 1.不等式 x 2 -3 x +2<0的解集为 ( ) A.(- ∞ ,-2) ∪ (-1,+ ∞ ) B.(-2,-1) C.(- ∞ ,1) ∪ (2,+ ∞ ) D.(1,2) 答案 D 将 x 2 -3 x +2<0化为( x -1)( x -2)<0, 解得1< x <2. 2.若不等式 mx 2 +2 x +1>0的解集为(- ∞ ,-2) ∪ ,则 m = ( ) A. B. C. D. 答案 C 由已知可得-2,- 为方程 mx 2 +2 x +1=0的两根,故 解得 m = ,故选C. 3.不等式 ≤ 0的解集为 ( ) A.{ x | x <1或 x ≥ 3} B.{ x |1 ≤ x ≤ 3} C.{ x |1< x ≤ 3} D.{ x |1< x <3} 答案 C 由 ≤ 0,得 解得1< x ≤ 3. 4.已知 f ( x )= ax 2 - x - c ,若不等式 f ( x )>0的解集为{ x |-2< x <1},则函数 y = f (- x )的 图象为 ( ) 答案 B 由题意知 ax 2 - x - c =0( a ≠ 0)的两根为-2,1.由根与系数的关系得 =-2+1,- =(-2) × 1,得 a =-1, c =-2,∴ f ( x )=- x 2 - x +2(经检验知满足题意),∴ f (- x )=- x 2 + x +2,其图象开口向下,顶点为 .故选B. 5.若集合 A ={ x | ax 2 - ax +1<0}= ⌀ ,则实数 a 的取值集合是 ( ) A.{ a |0< a <4} B.{ a |0 ≤ a <4} C.{ a |0< a ≤ 4} D.{ a |0 ≤ a ≤ 4} 答案 D a =0时,满足条件; a ≠ 0时,由题意知 a >0且 Δ = a 2 -4 a ≤ 0,得0< a ≤ 4,所以0 ≤ a ≤ 4,故选D. 考点一 一元二次不等式的解法 典例1 解下列不等式: (1)19 x -3 x 2 ≥ 6;(2)8 x -1 ≤ 16 x 2 ; (3)0< x 2 - x -2 ≤ 4;(4) ax 2 -( a +1) x +1<0. 考点突破 函数 y =3 x 2 -19 x +6的图象开口向上且与 x 轴有两个交点 和(6,0).所以 原不等式的解集为 . 解析 (1)解法一:原不等式可化为3 x 2 -19 x +6 ≤ 0. 解法二:原不等式可化为3 x 2 -19 x +6 ≤ 0, 即(3 x -1)( x -6) ≤ 0,所以 ( x -6) ≤ 0, 所以原不等式的解集为 . (2)8 x -1 ≤ 16 x 2 ⇔ 16 x 2 -8 x +1 ≥ 0 ⇔ (4 x -1) 2 ≥ 0, ∵对于任意的 x ∈R,原不等式都成立, ∴原不等式的解集为R. (3)原不等式等价于 ⇔ ⇔ ⇔ 利用数轴(如图)可知,原不等式的解集为{ x |-2 ≤ x <-1或2< x ≤ 3}. (4)原不等式可变形为( ax -1)( x -1)<0, 当 a =0时,原不等式的解集为{ x | x >1}; 当 a ≠ 0时,原不等式可变形为 a ( x -1)<0. 若 a <0,则 ( x -1)>0, ∴ x < 或 x >1. 若 a >0,则 ( x -1)<0, ∴当 a >1时,原不等式的解集为 ; 当 a =1时,原不等式的解集为 ⌀ ; 当0< a <1时,原不等式的解集为 . 综上,当 a <0时,原不等式的解集为 ; 当 a =0时,原不等式的解集为{ x | x >1}; 当0< a <1时,原不等式的解集为 ; 当 a =1时,原不等式的解集为 ⌀ ; 当 a >1时,原不等式的解集为 . 方法指导 1.解一元二次不等式的方法和步骤 (1)化:把不等式变形为二次项系数大于零的形式. (2)判:计算对应方程的判别式. (3)求:求出对应的一元二次方程的根,或根据判别式说明方程有没有实 根. (4)写:利用“大于取两边,小于取中间”写出不等式的解集. 2.解含参数的一元二次不等式时,要把握好分类讨论的层次,一般按下面 次序进行讨论:首先根据二次项系数的符号进行讨论;其次根据相应一 元二次方程的根是否存在,即 Δ 的符号进行讨论;最后在根存在时,根据 根的大小进行讨论. 1-1 不等式 ≥ 2的解集是 ( ) A. B. C. ∪ (1,3] D. ∪ (1,3] 答案 D 不等式可化为 ≤ 0, 即 ≤ 0, 解得- ≤ x <1或1< x ≤ 3,故选D. 1-2 已知函数 f ( x )= 则不等式 f ( x )- x ≤ 2的解集是 . 答案 解析 当 x ≤ 0时,原不等式等价于2 x 2 +1- x ≤ 2, ∴- ≤ x ≤ 0; 当 x >0时,原不等式等价于-2 x - x ≤ 2,∴ x >0. 综上所述, x ∈ . 考点二 一元二次不等式恒成立问题 命题角度一 形如 f ( x ) ≥ 0( x ∈R)恒成立,求参数范围 典例2 已知不等式 mx 2 -2 x - m +1<0.是否存在实数 m ,使对所有的实数 x 不 等式恒成立?若存在,求出 m 的取值范围;若不存在,请说明理由. 解析 不存在.理由:设 f ( x )= mx 2 -2 x - m +1. 不等式 mx 2 -2 x - m +1<0恒成立,即函数 f ( x )= mx 2 -2 x - m +1的图象全部在 x 轴下 方. 当 m =0时, f ( x )=1-2 x ,令1-2 x <0, 则 x > ,不满足题意; 当 m ≠ 0时,函数 f ( x )= mx 2 -2 x - m +1为二次函数, 需满足图象开口向下且方程 mx 2 -2 x - m +1=0无解, 即 此不等式组无解. 综上,不存在满足题意的 m . 典例3 设函数 f ( x )= mx 2 - mx -1( m ≠ 0),若对于 x ∈[1,3], f ( x )<- m +5恒成立, 求 m 的取值范围. 解析 f ( x )<- m +5即为 mx 2 - mx + m -6<0, 则问题转化为 mx 2 - mx + m -6<0在 x ∈[1,3]上恒成立, 有以下两种解法: 解法一:令 g ( x )= mx 2 - mx + m -6= m + m -6, x ∈[1,3]. 当 m >0时, g ( x )在[1,3]上是增函数. 所以 g ( x ) max = g (3)=7 m -6<0. 所以 m < ,则0< m < . 当 m <0时, g ( x )在[1,3]上是减函数, 命题角度二 形如 f ( x ) ≥ 0( x ∈[ a , b ])恒成立,求参数范围 所以 g ( x ) max = g (1)= m -6<0, 所以 m <6,所以 m <0. 综上所述, m 的取值范围是 . 解法二:因为 x 2 - x +1= + >0, 又因为 m ( x 2 - x +1)-6<0,所以 m < . 因为 y = = 在[1,3]上的最小值为 , 所以只需 m < 即可. 又因为 m ≠ 0,所以 m 的取值范围是 . 典例4 对任意 m ∈[-1,1],函数 f ( x )= x 2 +( m -4) x +4-2 m 的值恒大于零,求 x 的 取值范围. 命题角度三 形如 f ( x ) ≥ 0(参数 m ∈[ a , b ])恒成立,求 x 的范围 令 g ( m )=( x -2) m + x 2 -4 x +4. 由题意知在[-1,1]上, g ( m )的值恒大于零, ∴ 解得 x <1或 x >3. 故当 x <1或 x >3时,对任意的 m ∈[-1,1],函数 f ( x )的值恒大于零. 解析 f ( x )= x 2 +( m -4) x +4-2 m =( x -2) m + x 2 -4 x +4, 方法技巧 恒成立问题及二次不等式恒成立的条件 (1)解决恒成立问题一定要清楚选谁为主元,谁是参数,一般地,知道谁的 范围,就选谁当主元,求谁的范围,谁就是参数. (2)对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在 给定的区间上全部在 x 轴上方;恒小于0就是相应的二次函数的图象在给 定的区间上全部在 x 轴下方. 2-1 (2016甘肃白银会宁一中月考)不等式( a -2) x 2 +2( a -2) x -4<0对一切 x ∈R恒成立,则实数 a 的取值范围是 . 答案 (-2,2] 解析 当 a -2=0,即 a =2时,不等式即为-4<0,对一切 x ∈R恒成立, 当 a ≠ 2时,则有 解得-2< a <2. 综上,可得实数 a 的取值范围是(-2,2]. 2-2 已知函数 f ( x )= x 2 + mx -1,若对于任意 x ∈[ m , m +1],都有 f ( x )<0成立,则 实数 m 的取值范围是 . 答案 解析 要满足 f ( x )= x 2 + mx -1<0对于任意 x ∈[ m , m +1]恒成立, 只需 即 解得- < m <0.查看更多