2021届课标版高考文科数学大一轮复习精练:§9-3 椭圆及其性质(试题部分)
§9.3 椭圆及其性质
探考情 悟真题
【考情探究】
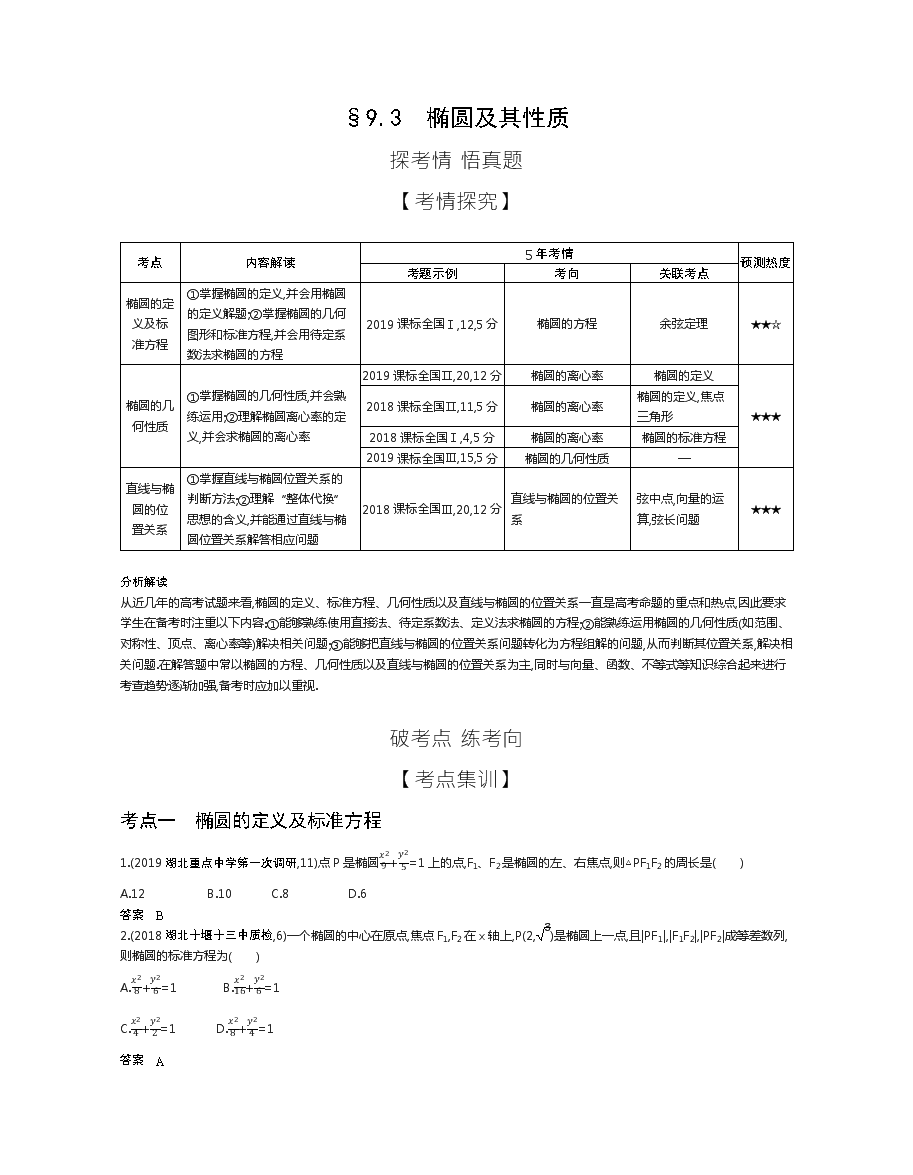
考点
内容解读
5年考情
预测热度
考题示例
考向
关联考点
椭圆的定
义及标
准方程
①掌握椭圆的定义,并会用椭圆的定义解题;②掌握椭圆的几何图形和标准方程,并会用待定系数法求椭圆的方程
2019课标全国Ⅰ,12,5分
椭圆的方程
余弦定理
★★☆
椭圆的几
何性质
①掌握椭圆的几何性质,并会熟练运用;②理解椭圆离心率的定义,并会求椭圆的离心率
2019课标全国Ⅱ,20,12分
椭圆的离心率
椭圆的定义
★★★
2018课标全国Ⅱ,11,5分
椭圆的离心率
椭圆的定义,焦点三角形
2018课标全国Ⅰ,4,5分
椭圆的离心率
椭圆的标准方程
2019课标全国Ⅲ,15,5分
椭圆的几何性质
—
直线与椭
圆的位
置关系
①掌握直线与椭圆位置关系的判断方法;②理解“整体代换”思想的含义,并能通过直线与椭圆位置关系解答相应问题
2018课标全国Ⅲ,20,12分
直线与椭圆的位置关系
弦中点,向量的运算,弦长问题
★★★
分析解读
从近几年的高考试题来看,椭圆的定义、标准方程、几何性质以及直线与椭圆的位置关系一直是高考命题的重点和热点,因此要求学生在备考时注重以下内容:①能够熟练使用直接法、待定系数法、定义法求椭圆的方程;②能熟练运用椭圆的几何性质(如范围、对称性、顶点、离心率等)解决相关问题;③能够把直线与椭圆的位置关系问题转化为方程组解的问题,从而判断其位置关系,解决相关问题.在解答题中常以椭圆的方程、几何性质以及直线与椭圆的位置关系为主,同时与向量、函数、不等式等知识综合起来进行考查趋势逐渐加强,备考时应加以重视.
破考点 练考向
【考点集训】
考点一 椭圆的定义及标准方程
1.(2019湖北重点中学第一次调研,11)点P是椭圆x29+y25=1上的点,F1、F2是椭圆的左、右焦点,则△PF1F2的周长是( )
A.12 B.10 C.8 D.6
答案 B
2.(2018湖北十堰十三中质检,6)一个椭圆的中心在原点,焦点F1,F2在x轴上,P(2,3)是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,则椭圆的标准方程为( )
A.x28+y26=1 B.x216+y26=1
C.x24+y22=1 D.x28+y24=1
答案 A
考点二 椭圆的几何性质
1.(2020届河南新乡、许昌两市第二次联考,4)焦点在x轴上的椭圆x2a2+y23=1(a>0)的离心率为22,则a=( )
A.6 B.6+32 C.6 D.32
答案 C
2.(2020届辽宁抚顺部分重点中学第二次联考,6)已知椭圆x2a2+y24=1的一个焦点坐标为(4,0),则a=( )
A.±25 B.±23 C.23 D.25
答案 A
3.(2020届百师联盟第一次联考,5)已知椭圆C:x2a2+y2b2=1(a>b>0),F1、F2为其左、右焦点,|F1F2|=22,B为短轴的一个端点,三角形BF1O(O为坐标原点)的面积为7,则椭圆的长轴长为( )
A.4 B.8 C.1+332 D.1+33
答案 B
4.(2018湖北武汉模拟,4)曲线x225+y29=1与曲线x225-k+y29-k=1(k<9)的( )
A.长轴长相等 B.短轴长相等
C.离心率相等 D.焦距相等
答案 D
5.(2015课标Ⅰ,5,5分)已知椭圆E的中心在坐标原点,离心率为12,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=( )
A.3 B.6 C.9 D.12
答案 B
考点三 直线与椭圆的位置关系
答案 A
2.过椭圆x25+y24=1的右焦点作一条斜率为2的直线与椭圆交于A,B两点,O为坐标原点,则△OAB的面积为 .
答案 53
炼技法 提能力
【方法集训】
方法1 求椭圆的标准方程的方法
1.(2020届江西南昌重点中学9月联考,8)椭圆C1:x2a2+y2b2=1(a>b>0)与双曲线C2:x2a2-y2b2=1的离心率之积为32,直线l:x-y+3=0与椭圆C1相切,则椭圆C1的方程为( )
A.x22+y2=1 B.x24+y22=1
C.x26+y23=1 D.x216+y28=1
答案 C
2.已知椭圆C的中心在原点,焦点在坐标轴上,且经过两点(2,-2),-1,142,则椭圆C的方程为 .
答案 x28+y24=1
方法2 求椭圆的离心率(或其取值范围)的方法
1.(2017课标全国Ⅲ,11,5分)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为( )
A.63 B.33 C.23 D.13
答案 A
2.(2018课标全国Ⅱ,11,5分)已知F1,F2是椭圆C的两个焦点,P是C上的一点.若PF1⊥PF2,且∠PF2F1=60°,则C的离心率为( )
A.1-32 B.2-3 C.3-12 D.3-1
答案 D
3.(2020届河南十所名校尖子生第二次联考,12)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别为A,B,点M为椭圆C上异于A,B的一点.直线AM和直线BM的斜率之积为-14,则椭圆C的离心率为( )
A.14 B.12 C.32 D.154
答案 C
4.设F1(-c,0)、F2(c,0)分别是椭圆x2a2+y2b2=1(a>b>0)的左、右焦点,若在直线x=a2c上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A.0,22 B.0,33 C.22,1 D.33,1
答案 D
方法3 解决弦中点问题的方法
1.(2019湖南郴州一模,11)已知椭圆x24+y2b2=1(0
b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
A.13 B.12 C.23 D.34
答案 A
5.(2019课标全国Ⅲ,15,5分)设F1,F2为椭圆C:x236+y220=1的两个焦点,M为C上一点且在第一象限.若△MF1F2为等腰三角形,则M的坐标为 .
答案 (3,15)
6.(2019课标全国Ⅱ,20,12分)已知F1,F2是椭圆C:x2a2+y2b2=1(a>b>0)的两个焦点,P为C上的点,O为坐标原点.
(1)若△POF2为等边三角形,求C的离心率;
(2)如果存在点P,使得PF1⊥PF2,且△F1PF2的面积等于16,求b的值和a的取值范围.
答案 本题主要考查椭圆的定义、简单的几何性质;考查数形结合的数学思想和逻辑思维能力与运算求解能力;体现了逻辑推理与数学运算的核心素养.
(1)连接PF1.由△POF2为等边三角形可知在△F1PF2中,∠F1PF2=90°,|PF2|=c,|PF1|=3c,于是2a=|PF1|+|PF2|=(3+1)c,故C的离心率e=ca=3-1.
(2)由题意可知,满足条件的点P(x,y)存在,当且仅当12|y|·2c=16,yx+c·yx-c=-1,x2a2+y2b2=1,
即c|y|=16,①
x2+y2=c2,②
x2a2+y2b2=1.③
由②③及a2=b2+c2得y2=b4c2,
又由①知y2=162c2,故b=4.
由②③得x2=a2c2(c2-b2),
所以c2≥b2,
从而a2=b2+c2≥2b2=32,故a≥42.
当b=4,a≥42时,存在满足条件的点P.
所以b=4,a的取值范围为[42,+∞).
7.(2018课标全国Ⅲ,20,12分)已知斜率为k的直线l与椭圆C:x24+y23=1交于A,B两点,线段AB的中点为M(1,m)(m>0).
(1)证明:k<-12;
(2)设F为C的右焦点,P为C上一点,且FP+FA+FB=0.证明:2|FP|=|FA|+|FB|.
答案 本题考查椭圆的几何性质、直线与椭圆的位置关系.
(1)设A(x1,y1),B(x2,y2),则x124+y123=1,x224+y223=1.
两式相减,并由y1-y2x1-x2=k得x1+x24+y1+y23·k=0.
由题设知x1+x22=1,y1+y22=m,于是k=-34m.
由题设得00)的直线交E于A,M两点,点N在E上,MA⊥NA.
(1)当|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,证明:30.
由已知及椭圆的对称性知,直线AM的倾斜角为π4.
又A(-2,0),因此直线AM的方程为y=x+2.(2分)
将x=y-2代入x24+y23=1得7y2-12y=0.
解得y=0或y=127,所以y1=127.
因此△AMN的面积S△AMN=2×12×127×127=14449.(4分)
(2)证明:将直线AM的方程y=k(x+2)(k>0)代入x24+y23=1得(3+4k2)x2+16k2x+16k2-12=0.
由x1·(-2)=16k2-123+4k2得x1=2(3-4k2)3+4k2,
故|AM|=|x1+2|1+k2=121+k23+4k2.
由题设,直线AN的方程为y=-1k(x+2),
故同理可得|AN|=12k1+k23k2+4.(7分)
由2|AM|=|AN|得23+4k2=k3k2+4,即4k3-6k2+3k-8=0.(9分)
设f(t)=4t3-6t2+3t-8,则k是f(t)的零点, f '(t)=12t2-12t+3=3(2t-1)2≥0,所以f(t)在(0,+∞)内单调递增.
又f(3)=153-26<0, f(2)=6>0,因此f(t)在(0,+∞)内有唯一的零点,且零点k在(3,2)内,所以3b>0)的焦点为F1(-1,0),F2(1,0).过F2作x轴的垂线l,在x轴的上方,l与圆F2:(x-1)2+y2=4a2交于点A,与椭圆C交于点D.连接AF1并延长交圆F2于点B,连接BF2交椭圆C于点E,连接DF1.已知DF1=52.
(1)求椭圆C的标准方程;
(2)求点E的坐标.
答案 本题主要考查直线方程、圆的方程、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识,考查推理论证能力、分析问题能力和运算求解能力.
(1)设椭圆C的焦距为2c.
因为F1(-1,0),F2(1,0),所以F1F2=2,c=1.
又因为DF1=52,AF2⊥x轴,所以DF2=DF12-F1F22=522-22=32.
因此2a=DF1+DF2=4,从而a=2.
由b2=a2-c2,得b2=3.
因此,椭圆C的标准方程为x24+y23=1.
(2)解法一:由(1)知,椭圆C:x24+y23=1,a=2.
因为AF2⊥x轴,所以点A的横坐标为1.
将x=1代入圆F2的方程(x-1)2+y2=16,解得y=±4.
因为点A在x轴上方,所以A(1,4).
又F1(-1,0),所以直线AF1:y=2x+2.
由y=2x+2,(x-1)2+y2=16,得5x2+6x-11=0,
解得x=1或x=-115.
将x=-115代入y=2x+2,得y=-125.
因此B-115,-125.
又F2(1,0),所以直线BF2:y=34(x-1).
由y=34(x-1),x24+y23=1,得7x2-6x-13=0,解得x=-1或x=137.
又因为E是线段BF2与椭圆的交点,所以x=-1.
将x=-1代入y=34(x-1),得y=-32.
因此E-1,-32.
解法二:由(1)知,椭圆C:x24+y23=1.
如图,连接EF1.
因为BF2=2a,EF1+EF2=2a,所以EF1=EB,
从而∠BF1E=∠B.
因为F2A=F2B,所以∠A=∠B.
所以∠A=∠BF1E,从而EF1∥F2A.
因为AF2⊥x轴,所以EF1⊥x轴.
因为F1(-1,0),由x=-1,x24+y23=1,
解得y=±32.
又因为E是线段BF2与椭圆的交点,所以y=-32.
因此E-1,-32.
3.(2018天津,19,14分)设椭圆x2a2+y2b2=1(a>b>0)的右顶点为A,上顶点为B.已知椭圆的离心率为53,|AB|=13.
(1)求椭圆的方程;
(2)设直线l:y=kx(k<0)与椭圆交于P,Q两点,l与直线AB交于点M,且点P,M均在第四象限.若△BPM的面积是△BPQ面积的2倍,求k的值.
答案 (1)设椭圆的焦距为2c,由已知有c2a2=59,又由a2=b2+c2,可得2a=3b.由|AB|=a2+b2=13,从而a=3,b=2.
所以,椭圆的方程为x29+y24=1.
(2)设点P的坐标为(x1,y1),点M的坐标为(x2,y2),由题意,x2>x1>0,点Q的坐标为(-x1,-y1).由△BPM的面积是△BPQ面积的2倍,可得|PM|=2|PQ|,从而x2-x1=2[x1-(-x1)],即x2=5x1.
易知直线AB的方程为2x+3y=6,由方程组2x+3y=6,y=kx,消去y,可得x2=63k+2.由方程组x29+y24=1,y=kx,消去y,可得x1=69k2+4.
由x2=5x1,可得9k2+4=5(3k+2),两边平方,整理得18k2+25k+8=0,解得k=-89或k=-12.
当k=-89时,x2=-9<0,不合题意,舍去;
当k=-12时,x2=12,x1=125,符合题意.
所以,k的值为-12.
考点二 椭圆的几何性质
1.(2016江苏,10,5分)如图,在平面直角坐标系xOy中,F是椭圆x2a2+y2b2=1(a>b>0)的右焦点,直线y=b2与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是 .
答案 63
2.(2019天津,19,14分)设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F,左顶点为A,上顶点为B.已知3|OA|=2|OB|(O为原点).
(1)求椭圆的离心率;
(2)设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为P,圆C同时与x轴和直线l相切,圆心C在直线x=4上,且OC∥AP.求椭圆的方程.
答案 本题主要考查椭圆的标准方程和几何性质、直线方程、圆等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想、数形结合思想解决问题的能力.
(1)设椭圆的半焦距为c,由已知有3a=2b.
又由a2=b2+c2,消去b得a2=32a2+c2,解得ca=12.
所以,椭圆的离心率为12.
(2)由(1)知,a=2c,b=3c,故椭圆方程为x24c2+y23c2=1.
由题意,F(-c,0),则直线l的方程为y=34(x+c).
点P的坐标满足x24c2+y23c2=1,y=34(x+c),消去y并化简,得到7x2+6cx-13c2=0,解得x1=c,x2=-13c7.
代入到l的方程,解得y1=32c,y2=-914c.
因为点P在x轴上方,所以Pc,32c.
由圆心C在直线x=4上,可设C(4,t).
因为OC∥AP,且由(1)知A(-2c,0),故t4=32cc+2c,解得t=2.则C(4,2).
因为圆C与x轴相切,所以圆的半径长为2,又由圆C与l相切,得34(4+c)-21+342=2,可得c=2.
所以,椭圆的方程为x216+y212=1.
考点三 直线与椭圆的位置关系
1.(2018江苏,18,14分)如图,在平面直角坐标系xOy中,椭圆C过点3,12,焦点F1(-3,0),F2(3,0),圆O的直径为F1F2.
(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于A,B两点.若△OAB的面积为267,求直线l的方程.
答案 解法一:(1)因为椭圆C的焦点为F1(-3,0),F2(3,0),
所以可设椭圆C的方程为x2a2+y2b2=1(a>b>0).
又点3,12在椭圆C上,所以3a2+14b2=1,a2-b2=3,
解得a2=4,b2=1.
因此,椭圆C的方程为x24+y2=1.
因为圆O的直径为F1F2,
所以其方程为x2+y2=3.
(2)①设直线l与圆O相切于P(x0,y0)(x0>0,y0>0),则x02+y02=3.
所以直线l的方程为y=-x0y0(x-x0)+y0,即y=-x0y0x+3y0.
由x24+y2=1,y=-x0y0x+3y0消去y,得
(4x02+y02)x2-24x0x+36-4y02=0.(*)
因为直线l与椭圆C有且只有一个公共点,所以Δ=(-24x0)2-4(4x02+y02)(36-4y02)=48y02(x02-2)=0.
因为x0,y0>0,所以x0=2,y0=1.
因此,点P的坐标为(2,1).
②因为三角形OAB的面积为267,所以12AB·OP=267,从而AB=427.
设A(x1,y1),B(x2,y2),
由(*)得
x1,2=24x0±48y02(x02-2)2(4x02+y02),
所以AB2=(x1-x2)2+(y1-y2)2=1+x02y02·48y02(x02-2)(4x02+y02)2.
因为x02+y02=3,
所以AB2=16(x02-2)(x02+1)2=3249,即2x04-45x02+100=0.
解得x02=52(x02=20舍去),则y02=12,因此P的坐标为102,22.
则直线l的方程为y=-5x+32.
解法二:(1)由题意知c=3,所以圆O的方程为x2+y2=3,因为点3,12在椭圆上,
所以2a=(3-3)2+12-02+(3+3)2+12-02=4,所以a=2.
因为a2=b2+c2,所以b=1,
所以椭圆C的方程为x24+y2=1.
(2)①由题意知直线l与圆O和椭圆C均相切,且切点在第一象限,所以直线l的斜率k存在且k<0,
设直线l的方程为y=kx+m(k<0,m>0),
将直线l的方程代入圆O的方程,得x2+(kx+m)2=3,
整理得(k2+1)x2+2kmx+m2-3=0,
因为直线l与圆O相切,所以Δ=(2km)2-4(k2+1)·(m2-3)=0,整理得m2=3k2+3,
将直线l的方程代入椭圆C的方程,得x24+(kx+m)2=1,
整理得(4k2+1)x2+8kmx+4m2-4=0,
因为直线l与椭圆C相切,
所以Δ=(8km)2-4(4k2+1)(4m2-4)=0,
整理得m2=4k2+1,
所以3k2+3=4k2+1,因为k<0,所以k=-2,则m=3,
将k=-2,m=3代入(k2+1)x2+2kmx+m2-3=0,
整理得x2-22x+2=0,
解得x1=x2=2,将x=2代入x2+y2=3,
解得y=1(y=-1舍去),所以点P的坐标为(2,1).
②设A(x1,kx1+m),B(x2,kx2+m),
由①知m2=3k2+3,且k<0,m>0,
因为直线l和椭圆C相交,所以结合②的过程知m2<4k2+1,解得k<-2,
将直线l的方程和椭圆C的方程联立可得(4k2+1)x2+8kmx+4m2-4=0,
解得x1,2=-8km±44k2+1-m22(4k2+1),
所以|x1-x2|=44k2+1-m24k2+1,
因为AB=(x1-x2)2+(kx1-kx2)2=|x1-x2|k2+1=44k2+1-m24k2+1·k2+1,
O到l的距离d=|m|k2+1=3,
所以S△OAB=12·44k2+1-m24k2+1·k2+1·|m|k2+1
=12·4k2-24k2+1·k2+1·3=267,
解得k2=5,因为k<0,所以k=-5,则m=32,
即直线l的方程为y=-5x+32.
2.(2018北京,20,14分)已知椭圆M:x2a2+y2b2=1(a>b>0)的离心率为63,焦距为22.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(1)求椭圆M的方程;
(2)若k=1,求|AB|的最大值;
(3)设P(-2,0),直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点Q-74,14共线,求k.
答案 (1)由题意得a2=b2+c2,ca=63,2c=22,
解得a=3,b=1.
所以椭圆M的方程为x23+y2=1.
(2)设直线l的方程为y=x+m,A(x1,y1),B(x2,y2).
由y=x+m,x23+y2=1
得4x2+6mx+3m2-3=0.
所以x1+x2=-3m2,x1x2=3m2-34.
|AB|=(x2-x1)2+(y2-y1)2=2(x2-x1)2
=2[(x1+x2)2-4x1x2]=12-3m22.
当m=0,即直线l过原点时,|AB|最大,最大值为6.
(3)设A(x1,y1),B(x2,y2).
由题意得x12+3y12=3,x22+3y22=3.
直线PA的方程为y=y1x1+2(x+2).
由y=y1x1+2(x+2),x2+3y2=3,
得[(x1+2)2+3y12]x2+12y12x+12y12-3(x1+2)2=0.
设C(xC,yC).
所以xC+x1=-12y12(x1+2)2+3y12=4x12-124x1+7.
所以xC=4x12-124x1+7-x1=-12-7x14x1+7.
所以yC=y1x1+2(xC+2)=y14x1+7.
设D(xD,yD).
同理得xD=-12-7x24x2+7,yD=y24x2+7.
记直线CQ,DQ的斜率分别为kCQ,kDQ,
则kCQ-kDQ=y14x1+7-14-12-7x14x1+7+74-y24x2+7-14-12-7x24x2+7+74=4(y1-y2-x1+x2).
因为C,D,Q三点共线,
所以kCQ-kDQ=0.
故y1-y2=x1-x2.
所以直线l的斜率k=y1-y2x1-x2=1.
C组 教师专用题组
考点一 椭圆的定义及标准方程
1.(2015广东,8,5分)已知椭圆x225+y2m2=1(m>0)的左焦点为F1(-4,0),则m=( )
A.2 B.3 C.4 D.9
答案 B
2.(2014大纲全国,9,5分)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点为F1、F2,离心率为33,过F2的直线l交C于A、B两点.若△AF1B的周长为43,则C的方程为( )
A.x23+y22=1 B.x23+y2=1
C.x212+y28=1 D.x212+y24=1
答案 A
3.(2016四川,20,13分)已知椭圆E:x2a2+y2b2=1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P3,12在椭圆E上.
(1)求椭圆E的方程;
(2)设不过原点O且斜率为12的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
答案 (1)由已知,a=2b.
又椭圆x2a2+y2b2=1(a>b>0)过点P3,12,
故34b2+14b2=1,解得b2=1.
所以椭圆E的方程是x24+y2=1.
(2)证明:设直线l的方程为y=12x+m(m≠0),A(x1,y1),B(x2,y2),
由方程组x24+y2=1,y=12x+m,得x2+2mx+2m2-2=0,①
方程①的判别式为Δ=4(2-m2),由Δ>0,即2-m2>0,解得-2b>0)的上顶点为B,左焦点为F,离心率为55.
(1)求直线BF的斜率;
(2)设直线BF与椭圆交于点P(P异于点B),过点B且垂直于BP的直线与椭圆交于点Q(Q异于点B),直线PQ与y轴交于点M,|PM|=λ|MQ|.
(i)求λ的值;
(ii)若|PM|sin∠BQP=759,求椭圆的方程.
答案 (1)设F(-c,0).由已知离心率ca=55及a2=b2+c2,可得a=5c,b=2c.
又因为B(0,b),F(-c,0),
故直线BF的斜率k=b-00-(-c)=2cc=2.
(2)设点P(xP,yP),Q(xQ,yQ),M(xM,yM).
(i)由(1)可得椭圆的方程为x25c2+y24c2=1,直线BF的方程为y=2x+2c.将直线方程与椭圆方程联立,消去y,整理得3x2+5cx=0,解得xP=-5c3.
因为BQ⊥BP,所以直线BQ的方程为y=-12x+2c,与椭圆方程联立,消去y,整理得21x2-40cx=0,解得xQ=40c21.
又因为λ=|PM||MQ|,及xM=0,可得λ=|xM-xP||xQ-xM|=|xP||xQ|=78.
(ii)由(i)有|PM||MQ|=78,所以|PM||PM|+|MQ|=77+8=715,
即|PQ|=157|PM|.
又因为|PM|sin∠BQP=759,
所以|BP|=|PQ|sin∠BQP=157|PM|sin∠BQP=553.
又因为yP=2xP+2c=-43c,
所以|BP|=0+5c32+2c+4c32=553c,
因此553c=553,得c=1.
所以,椭圆方程为x25+y24=1.
5.(2015重庆,21,12分)如图,椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.
(1)若|PF1|=2+2,|PF2|=2-2,求椭圆的标准方程;
(2)若|PQ|=λ|PF1|,且34≤λ<43,试确定椭圆离心率e的取值范围.
答案 (1)由椭圆的定义得,2a=|PF1|+|PF2|=(2+2)+(2-2)=4,故a=2.
设椭圆的半焦距为c,由已知PF1⊥PF2,因此
2c=|F1F2|=|PF1|2+|PF2|2=(2+2)2+(2-2)2=23,即c=3,从而b=a2-c2=1.
故所求椭圆的标准方程为x24+y2=1.
(2)如图,由PF1⊥PQ,|PQ|=λ|PF1|,得
|QF1|=|PF1|2+|PQ|2=1+λ2|PF1|.
由椭圆的定义得,|PF1|+|PF2|=2a,|QF1|+|QF2|=2a,进而
|PF1|+|PQ|+|QF1|=4a.
于是(1+λ+1+λ2)|PF1|=4a,
解得|PF1|=4a1+λ+1+λ2,
故|PF2|=2a-|PF1|=2a(λ+1+λ2-1)1+λ+1+λ2.
由勾股定理得
|PF1|2+|PF2|2=|F1F2|2=(2c)2=4c2,
从而4a1+λ+1+λ22+2a(λ+1+λ2-1)1+λ+1+λ22=4c2,
两边除以4a2,得
4(1+λ+1+λ2)2+(λ+1+λ2-1)2(1+λ+1+λ2)2=e2.
若记t=1+λ+1+λ2,则上式变成
e2=4+(t-2)2t2=81t-142+12.
由34≤λ<43,并注意到t=1+λ+1+λ2关于λ的单调性,得3≤t<4,即14<1t≤13.
进而12b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点.若|AF|+|BF|=4,点M到直线l的距离不小于45,则椭圆E的离心率的取值范围是( )
A.0,32 B.0,34 C.32,1 D.34,1
答案 A
3.(2013课标Ⅱ,5,5分)设椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( )
A.36 B.13 C.12 D.33
答案 D
4.(2012课标全国,4,5分)设F1、F2是椭圆E:x2a2+y2b2=1(a>b>0)的左、右焦点,P为直线x=3a2上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A.12 B.23 C.34 D.45
答案 C
5.(2011课标,4,5分)椭圆x216+y28=1的离心率为( )
A.13 B.12 C.33 D.22
答案 D
6.(2010全国Ⅰ,16,5分)已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交C于点D,且BF=2FD,则C的离心率为 .
答案 33
7.(2017天津,20,14分)已知椭圆x2a2+y2b2=1(a>b>0)的左焦点为F(-c,0),右顶点为A,点E的坐标为(0,c),△EFA的面积为b22.
(1)求椭圆的离心率;
(2)设点Q在线段AE上,|FQ|=32c,延长线段FQ与椭圆交于点P,点M,N在x轴上,PM∥QN,且直线PM与直线QN间的距离为c,四边形PQNM的面积为3c.
(i)求直线FP的斜率;
(ii)求椭圆的方程.
答案 (1)设椭圆的离心率为e.由已知,可得12(c+a)c=b22.
又由b2=a2-c2,可得2c2+ac-a2=0,即2e2+e-1=0.
又因为00),则直线FP的斜率为1m.
由(1)知a=2c,可得直线AE的方程为x2c+yc=1,即x+2y-2c=0,与直线FP的方程联立,可解得x=(2m-2)cm+2,y=3cm+2,即点Q的坐标为(2m-2)cm+2,3cm+2.由已知|FQ|=32c,有(2m-2)cm+2+c2+3cm+22=3c22,整理得3m2-4m=0,所以m=43,即直线FP的斜率为34.
(ii)由a=2c,可得b=3c,故椭圆方程可以表示为x24c2+y23c2=1.
由(i)得直线FP的方程为3x-4y+3c=0,与椭圆方程联立得3x-4y+3c=0,x24c2+y23c2=1,消去y,
整理得7x2+6cx-13c2=0,
解得x=-13c7(舍去),或x=c.因此可得点Pc,3c2,进而可得|FP|=(c+c)2+3c22=5c2,所以|PQ|=|FP|-|FQ|=5c2-3c2=c.
由已知,线段PQ的长即为PM与QN这两条平行直线间的距离,故直线PM和QN都垂直于直线FP.
因为QN⊥FP,所以|QN|=|FQ|·tan∠QFN=3c2×34=9c8,所以△FQN的面积为12|FQ||QN|=27c232,同理△FPM的面积等于75c232,由四边形PQNM的面积为3c,得75c232-27c232=3c,整理得c2=2c,又由c>0,得c=2.
所以,椭圆的方程为x216+y212=1.
8.(2015安徽,20,13分)设椭圆E的方程为x2a2+y2b2=1(a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足|BM|=2|MA|,直线OM的斜率为510.
(1)求E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点.证明:MN⊥AB.
答案 (1)由题设条件知,点M的坐标为23a,13b,
又kOM=510,从而b2a=510.
进而a=5b,c=a2-b2=2b.
故e=ca=255.
(2)证明:由N是AC的中点知,点N的坐标为a2,-b2,可得NM=a6,5b6.
又AB=(-a,b),从而有AB·NM=-16a2+56b2=16(5b2-a2).
由(1)的计算结果可知a2=5b2,
所以AB·NM=0,故MN⊥AB.
9.(2014课标Ⅱ,20,12分)设F1,F2分别是椭圆C:x2a2+y2b2=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直.直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为34,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
答案 (1)根据c=a2-b2及题设知Mc,b2a,2b2=3ac.
将b2=a2-c2代入2b2=3ac,解得ca=12或ca=-2(舍去).
故C的离心率为12.
(2)由题意,知原点O为F1F2的中点,MF2∥y轴,所以直线MF1与y轴的交点D(0,2)是线段MF1的中点,故b2a=4,即b2=4a,①
由|MN|=5|F1N|得|DF1|=2|F1N|.
设N(x1,y1),由题意知y1<0,则
2(-c-x1)=c,-2y1=2,即x1=-32c,y1=-1.
代入C的方程,得9c24a2+1b2=1.②
将①及c=a2-b2代入②得9(a2-4a)4a2+14a=1.
解得a=7,b2=4a=28.故a=7,b=27.
考点三 直线与椭圆的位置关系
1.(2017北京,19,14分)已知椭圆C的两个顶点分别为A(-2,0),B(2,0),焦点在x轴上,离心率为32.
(1)求椭圆C的方程;
(2)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4∶5.
答案 (1)设椭圆C的方程为x2a2+y2b2=1(a>b>0).
由题意得a=2,ca=32,解得c=3.
所以b2=a2-c2=1.
所以椭圆C的方程为x24+y2=1.
(2)证明:设M(m,n),则D(m,0),N(m,-n).
由题设知m≠±2,且n≠0.
直线AM的斜率kAM=nm+2,故直线DE的斜率kDE=-m+2n.
所以直线DE的方程为y=-m+2n(x-m).
直线BN的方程为y=n2-m(x-2).
联立y=-m+2n(x-m),y=n2-m(x-2),解得点E的纵坐标yE=-n(4-m2)4-m2+n2.
由点M在椭圆C上,得4-m2=4n2.
所以yE=-45n.
又S△BDE=12|BD|·|yE|=25|BD|·|n|,
S△BDN=12|BD|·|n|,
所以△BDE与△BDN的面积之比为4∶5.
2.(2016天津,19,14分)设椭圆x2a2+y23=1(a>3)的右焦点为F,右顶点为A.已知1|OF|+1|OA|=3e|FA|,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H.若BF⊥HF,且∠MOA=∠MAO,求直线l的斜率.
答案 (1)设F(c,0),由1|OF|+1|OA|=3e|FA|,即1c+1a=3ca(a-c),可得a2-c2=3c2,
又a2-c2=b2=3,所以c2=1,因此a2=4.
所以,椭圆的方程为x24+y23=1.
(2)设直线l的斜率为k(k≠0),
则直线l的方程为y=k(x-2).
设B(xB,yB),由方程组x24+y23=1,y=k(x-2)消去y,
整理得(4k2+3)x2-16k2x+16k2-12=0.
解得x=2,或x=8k2-64k2+3,由题意得xB=8k2-64k2+3,从而yB=-12k4k2+3.
由(1)知,F(1,0),设H(0,yH),有FH=(-1,yH),BF=9-4k24k2+3,12k4k2+3.
由BF⊥HF,得BF·FH=0,所以4k2-94k2+3+12kyH4k2+3=0,解得yH=9-4k212k.
因此直线MH的方程为y=-1kx+9-4k212k.
设M(xM,yM),由方程组y=k(x-2),y=-1kx+9-4k212k消去y,
解得xM=20k2+912(k2+1).
在△MAO中,∠MOA=∠MAO⇔|MA|=|MO|,即(xM-2)2+yM2=xM2+yM2,化简得xM=1,即20k2+912(k2+1)=1,解得k=-64,或k=64.
所以,直线l的斜率为-64或64.
【三年模拟】
时间:80分钟 分值:100分
一、选择题(每小题5分,共50分)
1.(2020届豫南九校第三次联考,4)若m是2和8的等比中项,则圆锥曲线x2+y2m=1的离心率为( )
A.32 B.5 C.32或52 D.32或5
答案 D
2.(2019湖北“荆、荆、襄、宜”四地七校考试联盟联考,4)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,离心率为12,过F2的直线与椭圆C交于A,B两点.若△F1AB的周长为8,则椭圆方程为( )
A.x24+y23=1 B.x216+y212=1
C.x22+y2=1 D.x24+y22=1
答案 A
3.(2018安徽合肥一模,7)如图,椭圆x2a2+y24=1的左、右焦点分别为F1,F2,过F1的直线交椭圆于M,N两点,交y轴于点H.若F1,H是线段MN的三等分点,则△F2MN的周长为( )
A.20 B.10 C.25 D.45
答案 D
4.(2020届陕西百校联盟9月联考,10)已知椭圆C:x28+y22=1的左、右焦点分别为F1,F2,直线l过点F2且与椭圆C交于M,N两点,且MA=AN,若|OA|=|AF2|,则直线l的斜率为( )
A.±1 B.±12 C.±13 D.±14
答案 B
5.(2020届黑龙江顶级名校11月联考,11)设椭圆x2a2+y2b2=1(a>b>0)的离心率e=12,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
A.必在圆x2+y2=2外 B.必在圆x2+y2=2上
C.必在圆x2+y2=2内 D.以上三种情形都有可能
答案 C
6.(2019广西南宁二中、柳州高中联考,8)已知圆F1:(x+2)2+y2=36,定点F2(2,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点,则P点的轨迹C的方程是( )
A.x24+y23=1 B.x29+y25=1
C.x23+y24=1 D.x25+y29=1
答案 B
7.(2020届西南地区名师联盟8月联考,11)如图所示,已知椭圆方程为x2a2+y2b2=1(a>b>0),A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率为( )
A.22 B.33 C.63 D.223
答案 C
8.(2020届河南百校联盟10月联考,11)已知椭圆C:x2a2+y2b2=1(a>b>0)的左,右焦点分别为F1,F2,点A是椭圆上一点,线段AF1的垂直平分线与椭圆的一个交点为B,若AB=3F2B,则椭圆C的离心率为( )
A.13 B.33 C.23 D.63
答案 B
9.(2020届安徽A10联盟摸底,11)已知椭圆C:x2a2+y2b2=1(a>b>0)上存在两点M、N关于直线2x-3y-1=0对称,且线段MN中点的纵坐标为23,则椭圆C的离心率是( )
A.13 B.33 C.23 D.223
答案 B
10.(2019贵州铜仁东部联盟诊断,11)已知椭圆x2a2+y2b2=1(a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈π12,5π12,则该椭圆的离心率e的取值范围是( )
A.22,63 B.33,22
C.12,33 D.23,63
答案 A
二、解答题(共50分)
11.(2020届河南、安徽部分重点中学10月联考,21)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1、F2,上顶点为A,△AF1F2的面积为1,且椭圆C的离心率为22.
(1)求椭圆C的标准方程;
(2)点M在椭圆上且位于第二象限,过点F1作直线l1⊥MF1,过点F2作直线l2⊥MF2,若直线l1,l2的交点N恰好在椭圆C上,求点M的坐标.
答案 (1)由题意可得ca=22,12·2c·b=1,a2-b2=c2,
结合a>b>0,解得a=2,b=1,c=1.(3分)
所以椭圆C的标准方程为x22+y2=1.(4分)
(2)由(1)知,F1(-1,0),F2(1,0).(5分)
设M(x0,y0),则x0<0,y0>0.
当x0=-1时,l2与l1相交于点F2,不符合题意.(6分)
当x0≠-1时,直线MF1的斜率为y0x0+1,直线MF2的斜率为y0x0-1.
因为l1⊥MF1,l2⊥MF2,所以直线l1的斜率为-x0+1y0,直线l2的斜率为-x0-1y0.(8分)
所以直线l1的方程为y=-x0+1y0(x+1),直线l2的方程为
y=-x0-1y0(x-1).
联立l1和l2的方程,解得x=-x0,y=x02-1y0,
所以N-x0,x02-1y0.(10分)
因为点M,N在椭圆C上,由椭圆的对称性,可知x02-1y0=±y0,所以x02-y02=1或x02+y02=1.
由x02-y02=1,x022+y02=1结合x0<0,y0>0,解得x0=-233,y0=33.而x02+y02=1,x022+y02=1无解,
所以点M的坐标为-233,33.(12分)
12.(2020届皖北协作体第二次联考,20)已知O为坐标原点,F为椭圆C:x24+y29=1的上焦点,C上一点A在第一象限,且|OA|=5.
(1)求直线AF的方程;
(2)若斜率为-12的直线l交椭圆C于不同的两点M、N,求△OMN面积的最大值.
答案 (1)设A(x0,y0)(x0>0,y0>0),因为|OA|=5,所以x02+y02=5,
又因为点A在椭圆上,所以x024+y029=1,
联立x02+y02=5,x024+y029=1,结合x0>0,y0>0,解得x0=455,y0=355,
故A的坐标为455,355.
又知F的坐标为(0,5),
所以直线AF的方程为y=-12x+5.
(2)设直线l:y=-12x+m,M(x1,y1),N(x2,y2).
由x24+y29=1,y=-12x+m得5x2-2mx+2m2-18=0,
由Δ>0,得-100,m>0)与椭圆C交于P,Q两点,且直线OP,PQ,OQ的斜率依次成等比数列,则当△OPQ的面积为74时,求直线PQ的方程.
答案 (1)设椭圆C的方程为x2a2+y2b2=1(a>b>0),
由题意可得c=3,由已知及|MF1|+|MF2|=2a,得a=2,
故b2=a2-c2=1,
∴椭圆C的方程为x24+y2=1.
(2)设P(x1,y1),Q(x2,y2).
联立y=kx+m,x24+y2=1得(1+4k2)x2+8kmx+4m2-4=0,
∴Δ=64k2m2-4(1+4k2)(4m2-4)>0,化简得m2<4k2+1①,
由根与系数的关系得x1+x2=-8km1+4k2,x1x2=4m2-41+4k2.
∵直线OP,PQ,OQ的斜率依次成等比数列,∴k2=y1x1·y2x2,
∴(kx1+m)(kx2+m)=k2x1x2,化简得mk(x1+x2)+m2=0,
∴-8k21+4k2+1=0,∴4k2=1,又k>0,∴k=12,
将k=12代入①得m2<2.
∵|PQ|=1+k2·(x1+x2)2-4x1x2=4(1+k2)(2-m2)1+4k2,
原点O到直线PQ的距离d=|m|1+k2,
∴S△OPQ=12|PQ|d=2|m|2-m21+4k2=|m|2-m2=74,
解得m=12或m=72m=-12,m=-72均舍去.
∴直线PQ的方程为y=12x+12或y=12x+72.
14.(命题标准样题,20)地球围绕太阳公转的轨道是一个椭圆,太阳位于该椭圆的一个焦点,每单位时间地球公转扫过椭圆内区域的面积相同.我国古代劳动人民根据长期的生产经验总结创立了二十四节气,将一年(地球围绕太阳公转一周)划分为24个节气,规则是:任意两个相邻节气地球与太阳的连线成15°角.地球在小寒前约三四天到达近日点,在小暑前约三四天到达远日点.
(1)从冬至到小寒与从夏至到小暑,哪一段时间更长?
(2)以立春为始,排在偶数位的十二个节气又称为中气.农历规定没有中气的那个月为闰月.经统计,1931年至2050年间,闰月最多的三个月份是:闰四月7次,闰五月9次,闰六月8次,闰月最少的三个月份是:闰十一月1次,闰十二月0次,闰一月0次.为什么会出现这种现象?请说明理由.
答案 本题是一道集数学、地理、物理内容于一体的综合题.试题以地球绕太阳公转的地理知识为背景,从中国古代流传下来的二十四节气入手,引入问题,涉及物理学的开普勒定律,利用数学中椭圆扇形的面积进行定量化的说明.试题考查了椭圆的性质,体现了理性思维、数学应用、数学探究的学科素养,考查了逻辑推理能力和直观想象能力,落实了综合性、应用性和创新性的考查要求.
(1)如图所示,太阳位于地球公转椭圆轨道的右焦点F,A,B,C,D分别为冬至,小寒(最接近近日点),夏至,小暑(最接近远日点)四个节气时地球所在的位置,则FB
查看更多