- 2021-06-02 发布 |
- 37.5 KB |
- 63页


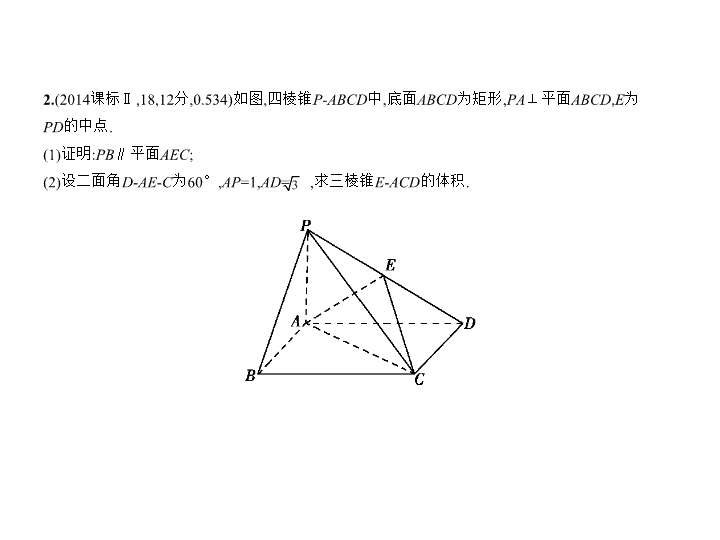
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考理数 直线、平面平行的判定与性质
§8.2 直线、平面平行的判定与性质 高考理数 (课标专用 ) A组 统一命题·课标卷题组 考点 直线、平面平行的判定与性质 1. (2016课标Ⅱ,14,5分) α , β 是两个平面, m , n 是两条直线,有下列四个命题: ①如果 m ⊥ n , m ⊥ α , n ∥ β ,那么 α ⊥ β . ②如果 m ⊥ α , n ∥ α ,那么 m ⊥ n . ③如果 α ∥ β , m ⊂ α ,那么 m ∥ β . ④如果 m ∥ n , α ∥ β ,那么 m 与 α 所成的角和 n 与 β 所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号) 五年高考 答案 ②③④ 解析 对于①,由 m ⊥ n , m ⊥ α 可得 n ∥ α 或 n 在 α 内,当 n ∥ β 时, α 与 β 可能相交,也可能平行,故①错 误;对于②,过直线 n 作平面与平面 α 交于直线 c ,由 n ∥ α 可知 n ∥ c ,∵ m ⊥ α ,∴ m ⊥ c ,∴ m ⊥ n ,故②正 确;对于③,由两个平面平行的性质可知正确;对于④,由线面所成角的定义和等角定理可知其 正确,故正确的有②③④. 解题关键 熟记和理解每个定理是解决此类问题的关键. 2. (2014课标Ⅱ,18,12分,0.534)如图,四棱锥 P - ABCD 中,底面 ABCD 为矩形, PA ⊥平面 ABCD , E 为 PD 的中点. (1)证明: PB ∥平面 AEC ; (2)设二面角 D - AE - C 为60 ° , AP =1, AD = ,求三棱锥 E - ACD 的体积. 解析 (1)证明:连接 BD 交 AC 于点 O ,连接 EO . 因为 ABCD 为矩形,所以 O 为 BD 的中点. 又 E 为 PD 的中点,所以 EO ∥ PB . 又 EO ⊂ 平面 AEC , PB ⊄ 平面 AEC ,所以 PB ∥平面 AEC . (2)因为 PA ⊥平面 ABCD , ABCD 为矩形,所以 AB , AD , AP 两两垂直. 如图,以 A 为坐标原点, 的方向为 x 轴的正方向,| |为单位长,建立空间直角坐标系 A - xyz ,则 D (0, ,0), E , = . 设 B ( m ,0,0)( m >0),则 C ( m , ,0), =( m , ,0). 设 n 1 =( x , y , z )为平面 ACE 的法向量, 则 即 可取 n 1 = . 又 n 2 =(1,0,0)为平面 DAE 的法向量,由题设得|cos< n 1 , n 2 >|= ,即 = ,解得 m = . 因为 E 为 PD 的中点,所以三棱锥 E - ACD 的高为 . 三棱锥 E - ACD 的体积 V = × × × × = . 思路分析 (1)在平面 AEC 内找出与 PB 平行的直线,分析题意可通过作三角形的中位线进行证 明;(2)要求三棱锥 E - ACD 的体积,易知三棱锥的高,又已知底面直角三角形的一直角边 AD 的长, 故只需求出另一直角边 CD 的长.可建立空间直角坐标系,利用向量法列方程(组)求解. 易错警示 对于第(2)问,二面角的平面角与两个半平面的法向量夹角相等或互补,部分同学容 易错误认为仅相等,另外,计算法向量时可能出错. 评析 本题考查线面平行的判定,利用空间向量解二面角问题,考查了学生的空间想象能力. 考点 直线、平面平行的判定与性质 1. (2018浙江,6,4分)已知平面 α ,直线 m , n 满足 m ⊄ α , n ⊂ α ,则“ m ∥ n ”是“ m ∥ α ”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 B组 自主命题·省(区、市)卷题组 答案 A ∵ m ⊄ α , n ⊂ α , m ∥ n ,∴ m ∥ α ,故充分性成立.而由 m ∥ α , n ⊂ α ,得 m ∥ n 或 m 与 n 异面,故 必要性不成立.故选A. 2 .(2016浙江,2,5分)已知互相垂直的平面 α , β 交于直线 l .若直线 m , n 满足 m ∥ α , n ⊥ β ,则 ( ) A. m ∥ l B. m ∥ n C. n ⊥ l D. m ⊥ n 答案 C 对于A, m 与 l 可能平行或异面,故A错;对于B、D, m 与 n 可能平行、相交或异面,故B、 D错;对于C,因为 n ⊥ β , l ⊂ β ,所以 n ⊥ l ,故C正确.故选C. 评析 本题考查了线面平行与垂直的性质及空间两条直线的位置关系. 3 .(2015福建,7,5分)若 l , m 是两条不同的直线, m 垂直于平面 α ,则“ l ⊥ m ”是“ l ∥ α ”的 ( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案 B 由已知知 m ⊥ α ,若 l ⊥ m ,则 l ∥ α 或 l ⊂ α .故充分性不成立.若 l ∥ α ,则一定有 l ⊥ m .故必要 性成立.选B. 4.( 2015安徽,5,5分)已知 m , n 是两条不同直线, α , β 是两个不同平面,则下列命题正确的是 ( ) A.若 α , β 垂直于同一平面,则 α 与 β 平行 B.若 m , n 平行于同一平面,则 m 与 n 平行 C.若 α , β ,则在 α 内 与 β 平行的直线 D.若 m , n ,则 m 与 n 垂直于同一平面 答案 D 若 α , β 垂直于同一个平面 γ ,则 α , β 可以都过 γ 的同一条垂线,即 α , β 可以相交,故A错;若 m , n 平行于同一个平面,则 m 与 n 可能平行,也可能相交,还可能异面,故B错;若 α , β 不平行,则 α , β 相 交,设 α ∩ β = l ,在 α 内存在直线 a ,使 a ∥ l ,则 a ∥ β ,故C错;从原命题的逆否命题进行判断,若 m 与 n 垂 直于同一个平面,由线面垂直的性质定理知 m ∥ n ,故D正确. 5. (2018江苏,15,14分)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中, AA 1 = AB , AB 1 ⊥ B 1 C 1 . 求证:(1) AB ∥平面 A 1 B 1 C ; (2)平面 ABB 1 A 1 ⊥平面 A 1 BC . 证明 本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想象 能力和推理论证能力. (1)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中, AB ∥ A 1 B 1 . 因为 AB ⊄ 平面 A 1 B 1 C , A 1 B 1 ⊂ 平面 A 1 B 1 C , 所以 AB ∥平面 A 1 B 1 C . (2)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中,四边形 ABB 1 A 1 为平行四边形. 又因为 AA 1 = AB ,所以四边形 ABB 1 A 1 为菱形,所以 AB 1 ⊥ A 1 B . 因为 AB 1 ⊥ B 1 C 1 , BC ∥ B 1 C 1 ,所以 AB 1 ⊥ BC . 又因为 A 1 B ∩ BC = B , A 1 B ⊂ 平面 A 1 BC , BC ⊂ 平面 A 1 BC , 所以 AB 1 ⊥平面 A 1 BC , 又因为 AB 1 ⊂ 平面 ABB 1 A 1 ,所以平面 ABB 1 A 1 ⊥平面 A 1 BC . 6 .(2017江苏,15,14分)如图,在三棱锥 A - BCD 中, AB ⊥ AD , BC ⊥ BD ,平面 ABD ⊥平面 BCD ,点 E , F ( E 与 A , D 不重合)分别在棱 AD , BD 上,且 EF ⊥ AD . 求证:(1) EF ∥平面 ABC ; (2) AD ⊥ AC . 证明 (1)在平面 ABD 内,因为 AB ⊥ AD , EF ⊥ AD ,所以 EF ∥ AB . 又因为 EF ⊄ 平面 ABC , AB ⊂ 平面 ABC ,所以 EF ∥平面 ABC . (2)因为平面 ABD ⊥平面 BCD ,平面 ABD ∩ 平面 BCD = BD , BC ⊂ 平面 BCD , BC ⊥ BD ,所以 BC ⊥平面 ABD . 因为 AD ⊂ 平面 ABD ,所以 BC ⊥ AD . 又 AB ⊥ AD , BC ∩ AB = B , AB ⊂ 平面 ABC , BC ⊂ 平面 ABC , 所以 AD ⊥平面 ABC . 又因为 AC ⊂ 平面 ABC ,所以 AD ⊥ AC . 方法总结 立体几何中证明线线垂直的一般思路: (1)利用两平行直线垂直于同一条直线( a ∥ b , a ⊥ c ⇒ b ⊥ c ); (2)线面垂直的性质( a ⊥ α , b ⊂ α ⇒ a ⊥ b ). 7. (2016四川,18,12分)如图,在四棱锥 P - ABCD 中, AD ∥ BC ,∠ ADC =∠ PAB =90 ° , BC = CD = AD , E 为棱 AD 的中点,异面直线 PA 与 CD 所成的角为90 ° . (1)在平面 PAB 内找一点 M ,使得直线 CM ∥平面 PBE ,并说明理由; (2)若二面角 P - CD - A 的大小为45 ° ,求直线 PA 与平面 PCE 所成角的正弦值. 解析 (1)在梯形 ABCD 中, AB 与 CD 不平行. 延长 AB , DC ,相交于点 M ( M ∈平面 PAB ),点 M 即为所求的一个点. 理由如下: 由已知, BC ∥ ED ,且 BC = ED . 所以四边形 BCDE 是平行四边形. 从而 CM ∥ EB .又 EB ⊂ 平面 PBE , CM ⊄ 平面 PBE , 所以 CM ∥平面 PBE . (说明:延长 AP 至点 N ,使得 AP = PN ,则所找的点可以是直线 MN 上任意一点) (2)解法一:由已知, CD ⊥ PA , CD ⊥ AD , PA ∩ AD = A , 所以 CD ⊥平面 PAD .从而 CD ⊥ PD . 所以∠ PDA 是二面角 P - CD - A 的平面角.所以∠ PDA =45 ° . 设 BC =1,则在Rt△ PAD 中, PA = AD =2. 过点 A 作 AH ⊥ CE ,交 CE 的延长线于点 H ,连接 PH . 易知 PA ⊥平面 ABCD ,又 CE ⊂ 平面 ABCD , 从而 PA ⊥ CE .于是 CE ⊥平面 PAH . 所以平面 PCE ⊥平面 PAH . 过 A 作 AQ ⊥ PH 于 Q ,则 AQ ⊥平面 PCE . 所以∠ APH 是 PA 与平面 PCE 所成的角. 在Rt△ AEH 中,∠ AEH =45 ° , AE =1,所以 AH = . 在Rt△ PAH 中, PH = = , 所以sin∠ APH = = . 解法二:由已知, CD ⊥ PA , CD ⊥ AD , PA ∩ AD = A , 所以 CD ⊥平面 PAD .于是 CD ⊥ PD . 从而∠ PDA 是二面角 P - CD - A 的平面角. 所以∠ PDA =45 ° .由 PA ⊥ AB ,可得 PA ⊥平面 ABCD . 设 BC =1,则在Rt△ PAD 中, PA = AD =2. 作 Ay ⊥ AD ,以 A 为原点,以 , 的方向分别为 x 轴, z 轴的正方向,建立如图所示的空间直角坐 标系 A - xyz , 则 A (0,0,0), P (0,0,2), C (2,1,0), E (1,0,0), 所以 =(1,0,-2), =(1,1,0), =(0,0,2). 设平面 PCE 的法向量为 n =( x , y , z ), 由 得 设 x =2,解得 n =(2,-2,1). 设直线 PA 与平面 PCE 所成角为 α , 则sin α = = = . 所以直线 PA 与平面 PCE 所成角的正弦值为 . 思路分析 对(1),延长 AB , DC 相交于一点 M ,则 M 在平面 PAB 内,由已知易知 CM ∥ EB ,从而 CM ∥ 平面 PBE ;对(2),有两种解法:解法一是传统几何方法,作出 PA 与面 PCE 所成的角,然后通过解三 角形求值;解法二是向量法,建立空间直角坐标系,求出面 PCE 的一个法向量 n ,利用sin α = 求值. 8.( 2015山东,17,12分)如图,在三棱台 DEF - ABC 中, AB =2 DE , G , H 分别为 AC , BC 的中点. (1)求证: BD ∥平面 FGH ; (2)若 CF ⊥平面 ABC , AB ⊥ BC , CF = DE ,∠ BAC =45 ° ,求平面 FGH 与平面 ACFD 所成的角(锐角)的 大小. 解析 (1)证法一:连接 DG , CD ,设 CD ∩ GF = O ,连接 OH . 在三棱台 DEF - ABC 中, AB =2 DE , G 为 AC 的中点,可得 DF ∥ GC , DF = GC ,所以四边形 DFCG 为平 行四边形. 则 O 为 CD 的中点,又 H 为 BC 的中点,所以 OH ∥ BD , 又 OH ⊂ 平面 FGH , BD ⊄ 平面 FGH ,所以 BD ∥平面 FGH . 证法二:在三棱台 DEF - ABC 中, 由 BC =2 EF , H 为 BC 的中点,可得 BH ∥ EF , BH = EF , 所以四边形 BHFE 为平行四边形,可得 BE ∥ HF . 在△ ABC 中, G 为 AC 的中点, H 为 BC 的中点,所以 GH ∥ AB . 又 GH ∩ HF = H ,所以平面 FGH ∥平面 ABED . 因为 BD ⊂ 平面 ABED ,所以 BD ∥平面 FGH . (2)解法一:设 AB =2,则 CF =1. 在三棱台 DEF - ABC 中, G 为 AC 的中点,由 DF = AC = GC ,可得四边形 DGCF 为平行四边形,因此 DG ∥ FC . 又 FC ⊥平面 ABC ,所以 DG ⊥平面 ABC . 在△ ABC 中,由 AB ⊥ BC ,∠ BAC =45 ° , G 是 AC 中点,所以 AB = BC , GB ⊥ GC ,因此 GB , GC , GD 两两垂 直. 以 G 为坐标原点,建立如图所示的空间直角坐标系 G - xyz . 所以 G (0,0,0), B ( ,0,0), C (0, ,0), D (0,0,1). 可得 H , F (0, ,1), 故 = , =(0, ,1). 设 n =( x , y , z )是平面 FGH 的法向量, 则由 可得 可得平面 FGH 的一个法向量 n =(1,-1, ). 因为 是平面 ACFD 的一个法向量, =( ,0,0), 所以cos< , n >= = = . 所以平面 FGH 与平面 ACFD 所成角(锐角)的大小为60 ° . 解法二:作 HM ⊥ AC 于点 M ,作 MN ⊥ GF 于点 N ,连接 NH . 由 FC ⊥平面 ABC ,得 HM ⊥ FC , 又 FC ∩ AC = C ,所以 HM ⊥平面 ACFD . 因此 GF ⊥ NH ,所以∠ MNH 即为所求的角. 在△ BGC 中, MH ∥ BG , MH = BG = , 由△ GNM ∽△ GCF ,可得 = ,从而 MN = . 由 HM ⊥平面 ACFD , MN ⊂ 平面 ACFD ,得 HM ⊥ MN , 因此tan∠ MNH = = ,所以∠ MNH =60 ° . 所以平面 FGH 与平面 ACFD 所成角(锐角)的大小为60 ° . 考点 直线、平面平行的判定与性质 1. (2013课标Ⅱ,4,5分,0.664)已知 m , n 为异面直线, m ⊥平面 α , n ⊥平面 β .直线 l 满足 l ⊥ m , l ⊥ n , l ⊄ α , l ⊄ β ,则 ( ) A. α ∥ β 且 l ∥ α B. α ⊥ β 且 l ⊥ β C. α 与 β 相交,且交线垂直于 l D. α 与 β 相交,且交线平行于 l C组 教师专用题组 答案 D 若 α ∥ β ,则 m ∥ n ,这与 m 、 n 为异面直线矛盾,所以A不正确, α 与 β 相交.将已知条件转 化到正方体中,易知 α 与 β 不一定垂直,但 α 与 β 的交线一定平行于 l ,从而排除B、C.故选D. 导师点睛 对于此类题,放入正方体中判断起来比较快捷. 2. (2016江苏,16,14分)如图,在直三棱柱 ABC - A 1 B 1 C 1 中, D , E 分别为 AB , BC 的中点,点 F 在侧棱 B 1 B 上,且 B 1 D ⊥ A 1 F , A 1 C 1 ⊥ A 1 B 1 . 求证:(1)直线 DE ∥平面 A 1 C 1 F ; (2)平面 B 1 DE ⊥平面 A 1 C 1 F . 证明 (1)在直三棱柱 ABC - A 1 B 1 C 1 中, A 1 C 1 ∥ AC . 在△ ABC 中,因为 D , E 分别为 AB , BC 的中点, 所以 DE ∥ AC ,于是 DE ∥ A 1 C 1 . 又因为 DE ⊄ 平面 A 1 C 1 F , A 1 C 1 ⊂ 平面 A 1 C 1 F , 所以直线 DE ∥平面 A 1 C 1 F . (2)在直三棱柱 ABC - A 1 B 1 C 1 中, A 1 A ⊥平面 A 1 B 1 C 1 . 因为 A 1 C 1 ⊂ 平面 A 1 B 1 C 1 ,所以 A 1 A ⊥ A 1 C 1 . 又因为 A 1 C 1 ⊥ A 1 B 1 , A 1 A ⊂ 平面 ABB 1 A 1 , A 1 B 1 ⊂ 平面 ABB 1 A 1 , A 1 A ∩ A 1 B 1 = A 1 , 所以 A 1 C 1 ⊥平面 ABB 1 A 1 . 因为 B 1 D ⊂ 平面 ABB 1 A 1 ,所以 A 1 C 1 ⊥ B 1 D . 又因为 B 1 D ⊥ A 1 F , A 1 C 1 ⊂ 平面 A 1 C 1 F , A 1 F ⊂ 平面 A 1 C 1 F , A 1 C 1 ∩ A 1 F = A 1 ,所以 B 1 D ⊥平面 A 1 C 1 F . 因为直线 B 1 D ⊂ 平面 B 1 DE ,所以平面 B 1 DE ⊥平面 A 1 C 1 F . 3. (2015江苏,16,14分)如图,在直三棱柱 ABC - A 1 B 1 C 1 中,已知 AC ⊥ BC , BC = CC 1 ,设 AB 1 的中点为 D , B 1 C ∩ BC 1 = E .求证: (1) DE ∥平面 AA 1 C 1 C ; (2) BC 1 ⊥ AB 1 . 证明 (1)由题意知, E 为 B 1 C 的中点, 又 D 为 AB 1 的中点,因此 DE ∥ AC . 又因为 DE ⊄ 平面 AA 1 C 1 C , AC ⊂ 平面 AA 1 C 1 C , 所以 DE ∥平面 AA 1 C 1 C . (2)因为棱柱 ABC - A 1 B 1 C 1 是直三棱柱, 所以 CC 1 ⊥平面 ABC . 因为 AC ⊂ 平面 ABC ,所以 AC ⊥ CC 1 . 又因为 AC ⊥ BC , CC 1 ⊂ 平面 BCC 1 B 1 , BC ⊂ 平面 BCC 1 B 1 , BC ∩ CC 1 = C ,所以 AC ⊥平面 BCC 1 B 1 . 又因为 BC 1 ⊂ 平面 BCC 1 B 1 ,所以 BC 1 ⊥ AC . 因为 BC = CC 1 ,所以矩形 BCC 1 B 1 是正方形, 因此 BC 1 ⊥ B 1 C . 因为 AC , B 1 C ⊂ 平面 B 1 AC , AC ∩ B 1 C = C , 所以 BC 1 ⊥平面 B 1 AC . 又因为 AB 1 ⊂ 平面 B 1 AC ,所以 BC 1 ⊥ AB 1 . 4 .(2015天津,17,13分)如图,在四棱柱 ABCD - A 1 B 1 C 1 D 1 中,侧棱 A 1 A ⊥底面 ABCD , AB ⊥ AC , AB =1, AC = A 1 =2, AD = CD = ,且点 M 和 N 分别为 B 1 C 和 D 1 D 的中点. (1)求证: MN ∥平面 ABCD ; (2)求二面角 D 1 - AC - B 1 的正弦值; (3)设 E 为棱 A 1 B 1 上的点.若直线 NE 和平面 ABCD 所成角的正弦值为 ,求线段 A 1 E 的长. 解析 如图,以 A 为原点建立空间直角坐标系, 依题意可得 A (0,0,0), B (0,1,0), C (2,0,0), D (1,-2,0), A 1 (0,0,2), B 1 (0,1,2), C 1 (2,0,2), D 1 (1,-2,2). 又因为 M , N 分别为 B 1 C 和 D 1 D 的中点,得 M , N (1,-2,1). (1)证明:依题意,可得 n =(0,0,1)为平面 ABCD 的一个法向量. = .由此可得 · n =0,又 因为直线 MN ⊄ 平面 ABCD ,所以 MN ∥平面 ABCD . (2) =(1,-2,2), =(2,0,0). 设 n 1 =( x , y , z )为平面 ACD 1 的法向量, 则 即 不妨设 z =1,可得 n 1 =(0,1,1). 设 n 2 =( x , y , z )为平面 ACB 1 的法向量, 则 又 =(0,1,2),得 不妨设 z =1,可得 n 2 =(0,-2,1). 因此有cos< n 1 , n 2 >= =- , 于是sin< n 1 , n 2 >= . 所以,二面角 D 1 - AC - B 1 的正弦值为 . (3)依题意,可设 = λ ,其中 λ ∈[0,1],则 E (0, λ ,2),从而 =(-1, λ +2,1).又 n =(0,0,1)为平面 ABCD 的一个法向量,由已知,得cos< , n >= = = ,整理得λ 2 +4λ-3=0, 又因为λ∈[0,1],解得λ= -2. 所以,线段 A 1 E 的长为 -2. 评析 本题主要考查直线与平面平行和垂直、二面角、直线与平面所成的角等基础知识. 考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算能力和推理论证能力. 5. (2013安徽,19,13分)如图,圆锥顶点为 P ,底面圆心为 O ,其母线与底面所成的角为22.5 ° , AB 和 CD 是底面圆 O 上的两条平行的弦,轴 OP 与平面 PCD 所成的角为60 ° . (1)证明:平面 PAB 与平面 PCD 的交线平行于底面; (2)求cos∠ COD . 解析 ( 1)证明:设面 PAB 与面 PCD 的交线为 l . 因为 AB ∥ CD , AB 不在面 PCD 内,所以 AB ∥面 PCD . 又因为 AB ⊂ 面 PAB ,面 PAB 与面 PCD 的交线为 l ,所以 AB ∥ l . 由直线 AB 在底面上而 l 在底面外可知, l 与底面平行. (2)设 CD 的中点为 F .连接 OF , PF . 由圆的性质,得∠ COD =2∠ COF , OF ⊥ CD . 因为 OP ⊥底面, CD ⊂ 底面,所以 OP ⊥ CD , 又 OP ∩ OF = O ,故 CD ⊥面 OPF . 又 CD ⊂ 面 PCD ,因此面 OPF ⊥面 PCD , 从而直线 OP 在面 PCD 上的射影为直线 PF ,故∠ OPF 为 OP 与面 PCD 所成的角. 由题设,知∠ OPF =60 ° . 设 OP = h ,则 OF = OP ·tan∠ OPF = h ·tan 60 ° = h . 根据题设有∠ OCP =22.5 ° , 得 OC = = . 由1=tan 45 ° = 和tan 22.5 ° >0, 可解得tan 22.5 ° = -1,因此 OC = =( +1) h . 在Rt△ OCF 中,cos∠ COF = = = - , 故cos∠ COD =cos 2∠ COF =2cos 2 ∠ COF -1=2( - ) 2 -1=17-12 . 评析 本题主要考查空间直线与直线、直线与平面、平面与平面间的位置关系,直线与平 面、直线与直线间所成角的计算等基础知识和基本技能,考查空间观念、推理论证能力和运 算求解能力. 6. (2013山东,18,12分)如图所示,在三棱锥 P - ABQ 中, PB ⊥平面 ABQ , BA = BP = BQ , D , C , E , F 分别是 AQ , BQ , AP , BP 的中点, AQ =2 BD , PD 与 EQ 交于点 G , PC 与 FQ 交于点 H ,连接 GH . (1)求证: AB ∥ GH ; (2)求二面角 D - GH - E 的余弦值. 解析 (1)证明:因为 D , C , E , F 分别是 AQ , BQ , AP , BP 的中点,所以 EF ∥ AB , DC ∥ AB . 所以 EF ∥ DC . 又 EF ⊄ 平面 PCD , DC ⊂ 平面 PCD ,所以 EF ∥平面 PCD . 又 EF ⊂ 平面 EFQ ,平面 EFQ ∩ 平面 PCD = GH ,所以 EF ∥ GH . 又 EF ∥ AB ,所以 AB ∥ GH . (2)解法一:在△ ABQ 中, AQ =2 BD , AD = DQ ,所以∠ ABQ =90 ° ,即 AB ⊥ BQ . 因为 PB ⊥平面 ABQ ,所以 AB ⊥ PB . 又 BP ∩ BQ = B ,所以 AB ⊥平面 PBQ . 由(1)知, AB ∥ GH ,所以 GH ⊥平面 PBQ . 又 FH ⊂ 平面 PBQ ,所以 GH ⊥ FH . 同理可得 GH ⊥ HC ,所以∠ FHC 为二面角 D - GH - E 的平面角. 设 BA = BQ = BP =2,连接 FC , 在Rt△ FBC 中,由勾股定理得 FC = , 在Rt△ PBC 中,由勾股定理得 PC = . 又 H 为△ PBQ 的重心, 所以 HC = PC = . 同理, FH = . 在△ FHC 中,由余弦定理得cos∠ FHC = =- . 即二面角 D - GH - E 的余弦值为- . 解法二:在△ ABQ 中, AQ =2 BD , AD = DQ , 所以∠ ABQ =90 ° . 又 PB ⊥平面 ABQ ,所以 BA , BQ , BP 两两垂直. 以 B 为坐标原点,分别以 BA , BQ , BP 所在直线为 x 轴, y 轴, z 轴,建立如图所示的空间直角坐标系. 设 BA = BQ = BP =2,则 E (1,0,1), F (0,0,1), Q (0,2,0), D (1,1,0), C (0,1,0), P (0,0,2). 所以 =(-1,2,-1), =(0,2,-1), =(-1,-1,2), =(0,-1,2). 设平面 EFQ 的法向量为 m =( x 1 , y 1 , z 1 ), 由 m · =0, m · =0, 得 取 y 1 =1,得 m =(0,1,2). 设平面 PDC 的法向量为 n =( x 2 , y 2 , z 2 ), 由 n · =0, n · =0, 得 取 z 2 =1,得 n =(0,2,1), 所以cos< m , n >= = . 因为二面角 D - GH - E 为钝二面角, 所以二面角 D - GH - E 的余弦值为- . 考点 直线、平面平行的判定与性质 1 .(2018安徽黄山二模,4)下列说法中,错误的是 ( ) A.若平面 α ∥平面 β ,平面 α ∩ 平面 γ = l ,平面 β ∩ 平面 γ = m ,则 l ∥ m B.若平面 α ⊥平面 β ,平面 α ∩ 平面 β = l , m ⊂ α , m ⊥ l ,则 m ⊥ β C.若直线 l ⊥平面 α ,平面 α ⊥平面 β ,则 l ∥ β D.若直线 l ∥平面 α ,平面 α ∩ 平面 β = m ,直线 l ⊂ 平面 β ,则 l ∥ m A组 2016—2018年高考模拟·基础题组 答案 C 对于A,由面面平行的性质定理可知为真命题,故A正确;对于B,由面面垂直的性质定 理可知为真命题,故B正确;对于C,若 l ⊥ α , α ⊥ β ,则 l ∥ β 或 l ⊂ β ,故C错误;对于D,由线面平行的性 质定理可知为真命题,故D正确.综上,选C. 三年模拟 2. (2018河南洛阳二模,4)若 m , n 是两条不同的直线, α , β 是两个不同的平面,则下列命题正确的是 ( ) A. m ⊥ α , n ⊥ β ,且 α ⊥ β ,则 m ∥ n B. m ⊥ α , n ∥ β 且 α ∥ β ,则 m ⊥ n C. m ∥ α , n ⊥ β 且 α ⊥ β ,则 m ∥ n D. m ∥ α , n ∥ β 且 α ∥ β ,则 m ∥ n 答案 B 对于A, m ⊥ α , α ⊥ β ,则 m ∥ β 或 m ⊂ β ,又 n ⊥ β ,则 n ⊥ m ,故A错;对于B, m ⊥ α , α ∥ β ,则 m ⊥ β , 又 n ∥ β ,所以 m ⊥ n ,故B正确;对于C,由 n ⊥ β , α ⊥ β ,可得 n ∥ α 或 n ⊂ α ,又 m ∥ α ,则 m 与 n 可能平行,可 能相交,也可能异面,故C错;对于D, m ∥ α , n ∥ β 且 α ∥ β ,则 m 与 n 可能平行,可能相交,也可能异面, 故D错.综上,选B. 3. (2017豫西五校4月联考,6)已知 m , n , l 1 , l 2 表示不同直线, α 、 β 表示不同平面,若 m ⊂ α , n ⊂ α , l 1 ⊂ β , l 2 ⊂ β , l 1 ∩ l 2 = M ,则 α ∥ β 的一个充分条件是 ( ) A. m ∥ β 且 l 1 ∥ α B. m ∥ β 且 n ∥ β C. m ∥ β 且 n ∥ l 2 D. m ∥ l 1 且 n ∥ l 2 答案 D 对于选项A,当 m ∥ β 且 l 1 ∥ α 时, α , β 可能平行也可能相交,故A不是 α ∥ β 的充分条件;对 于选项B,当 m ∥ β 且 n ∥ β 时,若 m ∥ n ,则 α , β 可能平行也可能相交,故B不是 α ∥ β 的充分条件;对于 选项C,当 m ∥ β 且 n ∥ l 2 时, α , β 可能平行也可能相交,故C不是 α ∥ β 的充分条件;对于选项D,当 m ∥ l 1 , n ∥ l 2 时,由线面平行的判定定理可得 l 1 ∥ α , l 2 ∥ α ,又 l 1 ∩ l 2 = M ,由面面平行的判定定理可以得到 α ∥ β ,但 α ∥ β 时, m ∥ l 1 且 n ∥ l 2 不一定成立,故D是 α ∥ β 的一个充分条件.故选D. 4 .(2016山西长治二模,5)已知 m , n 是两条不同的直线, α , β , γ 是三个不同的平面,则下列命题中正 确的是 ( ) A.若 α ⊥ γ , α ⊥ β ,则 γ ∥ β B.若 m ∥ n , m ⊂ α , n ⊂ β ,则 α ∥ β C.若 m ∥ n , m ⊥ α , n ⊥ β ,则 α ∥ β D.若 m ∥ n , m ∥ α ,则 n ∥ α 答案 C 对于A,墙角的三个墙面 α , β , γ 满足条件,但 γ 与 β 相交,故A错误; m ⊂ α , n ⊂ β ,且 m 、 n 平 行于 α , β 的交线时符合B中条件,但 α 与 β 相交,故B错误;由 m ∥ n , m ⊥ α 可推出 n ⊥ α ,结合 n ⊥ β 可推 出 α ∥ β ,故C选项正确;若 m ∥ n , m ∥ α ,则 n ∥ α 或 n ⊂ α ,故D错误.所以选C. 5. (2017河南洛阳一模,9)在直三棱柱 ABC - A 1 B 1 C 1 中,平面 α 与棱 AB , AC , A 1 C 1 , A 1 B 1 分别交于点 E , F , G , H ,且直线 AA 1 ∥平面 α .有下列三个命题:①四边形 EFGH 是平行四边形;②平面 α ∥平面 BCC 1 B 1 ;③平面 α ⊥平面 BCFE .其中正确的命题为 ( ) A.①② B.②③ C.①③ D.①②③ 答案 C AA 1 ∥平面 α ,平面 α ∩ 平面 AA 1 B 1 B = EH ,所以 AA 1 ∥ EH .同理, AA 1 ∥ GF ,所以 EH ∥ GF , 又由 ABC - A 1 B 1 C 1 是直三棱柱易知 EH = GF = AA 1 ,所以四边形 EFGH 是平行四边形,故①正确;若平 面 α ∥平面 BB 1 C 1 C ,由平面 α ∩ 平面 A 1 B 1 C 1 = GH ,平面 BCC 1 B 1 ∩ 平面 A 1 B 1 C 1 = B 1 C 1 ,知 GH ∥ B 1 C 1 ,而 由已知得不到 GH ∥ B 1 C 1 ,故②错误;由 AA 1 ⊥平面 BCFE ,结合 AA 1 ∥ EH 知 EH ⊥平面 BCFE ,又 EH ⊂ 平面 α ,所以平面 α ⊥平面 BCFE ,故③正确.综上,选C. 6. (2018河北唐山统一考试,14)在三棱锥 P - ABC 中, PB =6, AC =3, G 为△ PAC 的重心,过点 G 作三棱 锥的一个截面,使截面平行于 PB 和 AC ,则截面的周长为 . 答案 8 解析 过点 G 作 EF ∥ AC ,分别交 PA 、 PC 于点 E 、 F ,过 E 、 F 分别作 EN ∥ PB 、 FM ∥ PB ,分别交 AB 、 BC 于点 N 、 M ,连接 MN ,则四边形 EFMN 是平行四边形(面 EFMN 为所求截面),且 EF = MN = AC =2, FM = EN = PB =2,所以截面的周长为2 × 4=8. 7. (2018江西六校4月联考,18)在如图所示的几何体中,四边形 ABCD 为平行四边形,∠ ABD =90 ° , EB ⊥平面 ABCD , EF ∥ AB , AB =2, EB = , EF =1, BC = ,且 M 是 BD 的中点. (1)求证: EM ∥平面 ADF ; (2)求二面角 A - FD - B 的余弦值的大小. 解析 (1)证法一:取 AD 的中点 N ,连接 MN , NF . 在△ DAB 中, M 是 BD 的中点, N 是 AD 的中点, 所以 MN ∥ AB , MN = AB , 又因为 EF ∥ AB , EF = AB , 所以 MN ∥ EF 且 MN = EF . (2分) 所以四边形 MNFE 为平行四边形,所以 EM ∥ FN , (4分) 又因为 FN ⊂ 平面 ADF , EM ⊄ 平面 ADF ,故 EM ∥平面 ADF . (5分) 证法二:因为 EB ⊥平面 ABD , AB ⊥ BD ,故以 B 为原点,建立如图所示的空间直角坐标系 B - xyz . 由已知可得 = , =(3,-2,0), =(0,-1, ), 设平面 ADF 的法向量是 n =( x , y , z ). 由 得 令 y =3,则 n =(2,3, ). (2分) 又因为 · n =0,所以 ⊥ n , (4分) 又 EM ⊄ 平面 ADF ,故 EM ∥平面 ADF . (5分) (2)由(1)中证法二可知平面 ADF 的一个法向量是 n =(2,3, ). (6分) 易得平面 BFD 的一个法向量是 m =(0,- ,1). (9分) 所以cos< m , n >= =- , (11分) 又二面角 A - FD - B 为锐角, 故二面角 A - FD - B 的余弦值大小为 . (12分) ( 时间:40分钟 分值:50分) 一、选择题(每题5分,共15分) B组 2016—2018年高考模拟·综合题组 1. (2018山东泰安二模,9)已知 m , n 是两条不同直线, α , β , γ 是三个不同平面,下列命题正确的是 ( ) A.若 m ∥ α , n ∥ α ,则 m ∥ n B.若 α ⊥ γ , β ⊥ γ ,则 α ∥ β C.若 m ∥ α , m ∥ β ,则 α ∥ β D.若 m ⊥ α , n ⊥ α ,则 m ∥ n 答案 D 对于A,若 m ∥ α , n ∥ α ,则 m 与 n 可能平行,可能相交,也可能异面,故A错误;对于B,若 α ⊥ γ , β ⊥ γ ,则 α 与 β 可能平行,也可能相交(比如直三棱柱相邻两侧面都与底面垂直),故B错误;对 于C,若 m ∥ α , m ∥ β ,则 α 与 β 可能平行,也可能相交,故C错误;对于D,垂直于同一平面的两条直线 相互平行,故D正确.综上,选D. 方法总结 对点、线、面的位置关系的判断,常采用穷举法,即对各种位置关系都进行考虑,要 充分应用几何模型的直观作用. 2. (2018湖南长沙长郡中学模拟,11)如图,在四棱锥 P - ABCD 中, AB ⊥ AD , BC ∥ AD , PA = AD =4, AB = BC =2, PA ⊥平面 ABCD ,点 E 是线段 AB 的中点,点 F 在线段 PA 上,且 EF ∥平面 PCD ,直线 PD 与平面 CEF 交于点 H ,则线段 CH 的长度为 ( ) A. B.2 C.2 D.2 答案 C ∵ PD 与平面 CEF 交于点 H ,∴平面 CEF ∩ 平面 PCD = CH ,∵ EF ∥平面 PCD ,∴ EF ∥ CH ,过点 H 作 HM ∥ PA 交 AD 于点 M ,连接 CM ,∵ EF ∩ AF = F , CH ∩ HM = H ,∴平面 AEF ∥平面 CHM ,∵平面 AEF ∩ 平面 ABCD = AE ,平面 CHM ∩ 平面 ABCD = CM ,∴ AE ∥ CM ,又 BC ∥ AM ,∴四边形 ABCM 为平行 四边形,∴ AM =2.又 AD =4,∴ M 是 AD 的中点,则 H 为 PD 的中点,∴ CH = = =2 ,故选C. 一题多解 取 PA 的中点为 M , PD 的中点为 N ,连接 MN , BM , NC ,由三角形中位线的性质可得 MN ∥ AD ,且 MN = AD .又∵ BC ∥ AD ,且 BC = AD ,∴ MN查看更多