浙江省2021版高考物理一轮复习第十二章动量动量守恒定律第2节动量守恒定律碰撞爆炸反冲达标检测含解析 1

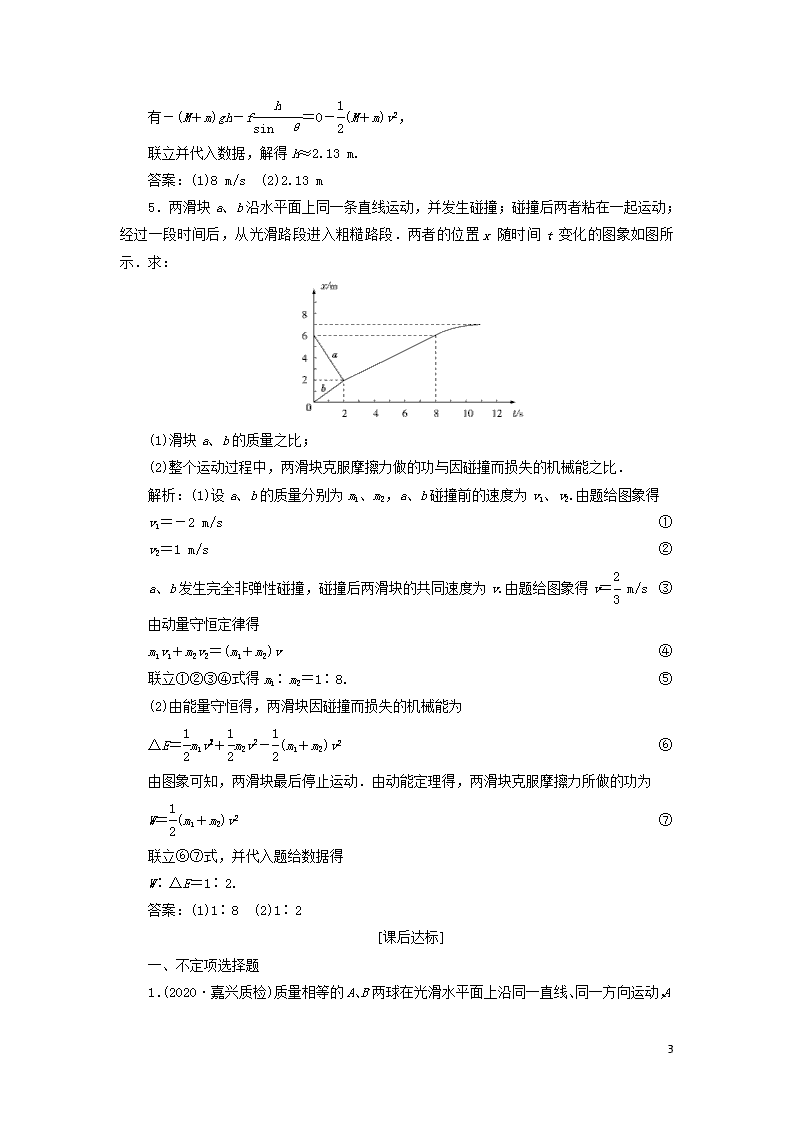
浙江省2021版高考物理一轮复习第十二章动量动量守恒定律第2节动量守恒定律碰撞爆炸反冲达标检测含解析 1

第2节 动量守恒定律 碰撞 爆炸 反冲 ‎1．一弹丸在飞行到距离地面5 m高时仅有水平速度v＝2 m/s，爆炸成为甲、乙两块水平飞出，甲、乙的质量比为3∶1，不计质量损失，取重力加速度g＝10 m/s2.则下列图中两块弹片飞行的轨迹可能正确的是(　　)‎ 解析：选B.弹丸爆炸瞬间爆炸力远大于外力，故爆炸瞬间动量守恒．因两弹片均水平飞出，飞行时间t＝ ＝1 s，取向右为正，由水平速度v＝知，选项A中，v甲＝2.5 m/s，v乙＝－0.5 m/s；选项B中，v甲＝2.5 m/s，v乙＝0.5 m/s；选项C中，v甲＝1 m/s，v乙＝2 m/s；选项D中，v甲＝－1 m/s，v乙＝2 m/s.因爆炸瞬间动量守恒，故mv＝m甲v甲＋m乙v乙，其中m甲＝m，m乙＝m，v＝2 m/s，代入数值计算知选项B正确．‎ ‎2．(2020·金华质检)如图所示，游乐场上，两位同学各驾着一辆碰碰车迎面相撞，此后，两车以共同的速度运动；设甲同学和他的车的总质量为150 kg，碰撞前向右运动，速度的大小为4.5 m/s，乙同学和他的车的总质量为200 kg，碰撞前向左运动，速度的大小为4.25 m/s，则碰撞后两车共同的运动速度为(取向右为正方向)(　　)‎ A．1 m/s　　　　　　　　　　 B．0.5 m/s C．－1 m/s D．－0.5 m/s 解析：选D.两车碰撞过程动量守恒 m1v1－m2v2＝(m1＋m2)v 得v＝＝ m/s ‎＝－0.5 m/s，故D正确．‎ ‎3．(2020·绍兴联考)如图所示，两小车A、B置于光滑水平面上，质量分别为m和2m，一轻质弹簧两端分别固定在两小车上，开始时弹簧处于拉伸状态，用手固定两小车．现在先释放小车B，当小车B的速度大小为3v时，再释放小车A，此时弹簧仍处于拉伸状态；当小车A的速度大小为v时，‎ 7‎ 弹簧刚好恢复原长．自始至终弹簧都未超出弹性限度．求：‎ ‎(1)弹簧刚恢复原长时，小车B的速度大小；‎ ‎(2)两小车相距最近时，小车A的速度大小；‎ ‎(3)两小车相距最近时，弹簧弹性势能大小．‎ 解析：(1)设弹簧刚恢复原长时，小车B速度为vB，以A、B两车和弹簧为研究对象，小车B速度为3v开始到小车A速度为v过程，此系统动量守恒，列方程有：‎ ‎2m·3v＝2m·vB＋m(－v)‎ 解得vB＝3.5v；‎ ‎(2)两小车相距最近时速度相同，由动量守恒定律有：‎ ‎2m×3v＝(2m＋m)vA 解得vA＝2v；‎ ‎(3)从弹簧刚恢复原长到两小车相距最近过程用能量守恒定律有 E弹＝×2mv＋mv2－×3m·v 解得E弹＝mv2.‎ 答案：(1)3.5v　(2)2v　(3)mv2‎ ‎4．如图所示，光滑水平面AB与粗糙斜面BC在B处通过圆弧衔接，质量M＝0.3 kg的小木块静止在水平面上的A点．现有一质量m＝0.2 kg的子弹以v0＝20 m/s的初速度水平射入木块(但未穿出)，它们一起沿AB运动，并冲上BC.已知木块与斜面间的动摩擦因数μ＝0.5，斜面倾角θ＝45°，重力加速度g取10 m/s2，木块在B处无机械能损失．试求：‎ ‎(1)子弹射入木块后的共同速度的大小；‎ ‎(2)子弹和木块能冲上斜面的最大高度．‎ 解析：(1)子弹射入木块的过程中，子弹与木块系统动量守恒，设向右为正方向，共同速度为v，则mv0＝(m＋M)v，代入数据解得v＝8 m/s.‎ ‎(2)子弹与木块以v的初速度冲上斜面，到达最大高度时，瞬时速度为零，子弹和木块在斜面上受到的支持力N＝(M＋m)gcos θ，‎ 受到的摩擦力f＝μN＝μ(M＋m)gcos θ.‎ 对冲上斜面的过程应用动能定理，设最大高度为h，‎ 有－(M＋m)gh－f＝0－(M＋m)v2，‎ 联立并代入数据，解得h≈2.13 m.‎ 7‎ 答案：(1)8 m/s　(2)2.13 m ‎5．两滑块a、b沿水平面上同一条直线运动，并发生碰撞；碰撞后两者粘在一起运动；经过一段时间后，从光滑路段进入粗糙路段．两者的位置x随时间t变化的图象如图所示．求：‎ ‎(1)滑块a、b的质量之比；‎ ‎(2)整个运动过程中，两滑块克服摩擦力做的功与因碰撞而损失的机械能之比．‎ 解析：(1)设a、b的质量分别为m1、m2，a、b碰撞前的速度为v1、v2.由题给图象得 v1＝－2 m/s ①‎ v2＝1 m/s ②‎ a、b发生完全非弹性碰撞，碰撞后两滑块的共同速度为v.由题给图象得v＝ m/s ③‎ 由动量守恒定律得 m1v1＋m2v2＝(m1＋m2)v ④‎ 联立①②③④式得m1∶m2＝1∶8. ⑤‎ ‎(2)由能量守恒得，两滑块因碰撞而损失的机械能为 ΔE＝m1v＋m2v－(m1＋m2)v2 ⑥‎ 由图象可知，两滑块最后停止运动．由动能定理得，两滑块克服摩擦力所做的功为 W＝(m1＋m2)v2 ⑦‎ 联立⑥⑦式，并代入题给数据得 W∶ΔE＝1∶2.‎ 答案：(1)1∶8　(2)1∶2‎ ‎[课后达标]‎ 一、不定项选择题 ‎1．(2020·嘉兴质检)质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动，A球的动量是7 kg·m/s，B球的动量是5 kg·m/s，A球追上B球发生碰撞，则碰撞后A、B两球的动量可能值是(　　)‎ A．p′A＝6 kg·m/s，p′B＝6 kg·m/s B．p′A＝3 kg·m/s，p′B＝9 kg·m/s 7‎ C．p′A＝－2 kg·m/s，p′B＝14 kg·m/s D．p′A＝－4 kg·m/s，p′B＝17 kg·m/s 答案：A ‎2．(2020·台州调研)如图所示，子弹水平射入放在光滑水平地面上静止的木块，子弹未穿透木块，此过程木块的动能增加了6 J，那么此过程中产生的内能可能为(　　)‎ A．16 J　　　 B．2 J　　　‎ C．6 J　　　 D．4 J 答案：A ‎3．(2020·浙江十校联考)将静置在地面上，质量为M(含燃料)的火箭模型点火升空，在极短时间内以相对地面的速度v0竖直向下喷出质量为m的炽热气体．忽略喷气过程重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是(　　)‎ A. v0 B. v0‎ C. v0 D. v0‎ 答案：D ‎4．(2020·金华质检)两球A、B在光滑水平面上沿同一直线、同一方向运动，mA＝1 kg，mB＝2 kg、vA＝6 m/s、vB＝2 m/s.当A追上B并发生碰撞后，两球A、B速度的可能值是(　　)‎ A．v′A＝5 m/s，v′B＝2.5 m/s B．v′A＝2 m/s，v′B＝4 m/s C．v′A＝－4 m/s，v′B＝7 m/s D．v′A＝7 m/s，v′B＝1.5 m/s 解析：选B.虽然题中四个选项均满足动量守恒定律，但A、D两项中，碰后A的速度v′A大于B的速度v′B，必然要发生第二次碰撞，不符合实际；C项中，两球碰后的总动能Ek′＝mAv′＋mBv′＝57 J，大于碰前的总动能Ek＝mAv＋mBv＝22 J，违背了能量守恒定律；而B项既符合实际情况，也不违背能量守恒定律，故B项正确．‎ ‎5．一中子与一质量数为A (A>1)的原子核发生弹性正碰．若碰前原子核静止，则碰撞前与碰撞后中子的速率之比为(　　)‎ A. B. C. D. 7‎ 解析：选A.设中子的质量为m，则被碰原子核的质量为Am，两者发生弹性碰撞，据动量守恒，有mv0＝mv1＋Amv′，据动能守恒，有mv＝mv＋Amv′2.解以上两式得v1＝v0.若只考虑速度大小，则中子的速率为v′1＝v0，故中子碰撞前、后速率之比为.‎ ‎6.(2020·温州质检)如图所示，放在光滑水平桌面上的两个木块A、B中间夹一被压缩的弹簧，当弹簧被放开时，它们各自在桌面上滑行一段距离后飞离桌面落在地上．A的落地点与桌边的水平距离为0.5 m，B的落地点与桌边的水平距离为1 m，那么(　　)‎ A．A、B离开弹簧时的速度之比为1∶2‎ B．A、B质量之比为2∶1‎ C．未离开弹簧时，A、B所受冲量之比为1∶2‎ D．未离开弹簧时，A、B加速度之比为1∶2‎ 解析：选ABD.A、B组成的系统在水平方向上不受外力，动量守恒，A、B两物体的落地点到桌边的距离x＝v0t，因为两物体的落地时间相等，所以v0与x成正比，故vA∶vB＝1∶2，即A、B离开弹簧时的速度之比．由动量守恒定律可知，mA∶mB＝2∶1.未离开弹簧时，A、B受到的弹力相等，作用时间相同，冲量大小也相同．未离开弹簧时，F相等，m不同，加速度a＝，与质量成反比，故aA∶aB＝1∶2，故A、B、D正确，C错误．‎ ‎7．对下列几种物理现象的解释，正确的是(　　)‎ A．击钉时，不用橡皮锤仅仅是因为橡皮锤太轻 B．跳远时，在沙坑里填沙，是为了减小冲量 C．易碎品运输时，要用柔软材料包装，船舷常常悬挂旧轮胎，都是为了延长作用时间以减小作用力 D．在车内推车推不动，是因为合外力冲量为零 解析：选CD.击钉时，不用橡皮锤是因为橡皮锤与钉子的作用时间长；跳远时，在沙坑里填沙，是为了延长人与地的接触时间，所以A、B错误；据动量定理F·t＝Δp知，当Δp相同时，作用时间越长，作用力越小，故C项正确；车能否移动或运动状态能否改变取决于外力的作用，与内部作用无关，所以D项正确．‎ ‎8.质量为M、内壁间距为L的箱子静止于光滑的水平面上，箱子中间有一质量为m的小物块，小物块与箱子底板间的动摩擦因数为μ.初始时小物块停在箱子正中间，如图所示．现给小物块一水平向右的初速度v，小物块与箱壁碰撞N次后恰又回到箱子正中间，并与箱子保持相对静止．设碰撞都是弹性的，则整个过程中，系统损失的动能为(　　)‎ A.mv2 B.v2‎ 7‎ C.NμmgL D．NμmgL 解析：选BD.设系统损失的动能为ΔE，根据题意可知，整个过程中小物块和箱子构成的系统满足动量守恒和能量守恒，则有mv＝(M＋m)vt(①式)、mv2＝(M＋m)v＋ΔE(②式)，由①②联立解得ΔE＝v2，可知选项A错误，B正确；又由于小物块与箱壁碰撞为弹性碰撞，则损耗的能量全部用于摩擦生热，即ΔE＝NμmgL，选项C错误，D正确．‎ 二、非选择题 ‎9．(2020·杭州质检)如图所示，一质量为0.5 kg的小球A以2.0 m/s的速度和静止于光滑水平面上、质量为1 kg的另一大小相同的小球B发生正碰，碰撞后它以0.2 m/s 的速度反弹．求：‎ ‎(1)原来静止小球B获得的速度大小；‎ ‎(2)碰撞过程中损失的机械能．‎ 解析：(1)A、B两小球碰撞过程中动量守恒，设小球B的速度为v，则mAvA＝mAvA′＋mBv，‎ 代入数据解得v＝1.1 m/s.‎ ‎(2)由A、B两小球组成的系统能量守恒有 mAv＝mAv′＋mBv2＋ΔE 解得ΔE＝0.385 J.‎ 答案：(1)1.1 m/s　(2)0.385 J ‎10．如图所示，一质量M＝2 kg的带有弧形轨道的平台置于足够长的水平轨道上，弧形轨道与水平轨道平滑连接，水平轨道上静置一小球B.从弧形轨道上距离水平轨道高h＝0.3 m处由静止释放一质量mA＝1 kg的小球A，小球A沿轨道下滑后与小球B发生弹性正碰，碰后小球A被弹回，且恰好追不上平台．已知所有接触面均光滑，重力加速度为g.求小球B的质量．(取重力加速度g＝10 m/s2)‎ 解析：设小球A下滑到水平轨道上时的速度大小为v1，平台水平速度大小为v，由动量守恒定律有0＝mAv1－Mv 由能量守恒定律有 mAgh＝mAv＋Mv2‎ 联立解得v1＝2 m/s，v＝1 m/s 小球A、B碰后运动方向相反，设小球A、B的速度大小分别为v′1和v2.由于碰后小球A被弹回，且恰好追不上平台，则此时小球A的速度等于平台的速度，有v′1＝1 m/s 7‎ 由动量守恒定律得mAv1＝－mAv′1＋mBv2‎ 由能量守恒定律有 mAv＝mAv′＋mBv 联立上式解得mB＝3 kg.‎ 答案：3 kg ‎11.(2020·宁波质检)如图，质量分别为mA、mB的两个弹性小球A、B静止在地面上方，B球距地面的高度h＝0.8 m，A球在B球的正上方．先将B球释放，经过一段时间后再将A球释放．当A球下落t＝0.3 s时，刚好与B球在地面上方的P点处相碰．碰撞时间极短，碰后瞬间A球的速度恰好为零．已知mB＝3mA，重力加速度大小g＝10 m/s2，忽略空气阻力及碰撞中的动能损失．求：‎ ‎(1)B球第一次到达地面时的速度；‎ ‎(2)P点距离地面的高度．‎ 解析：(1)设B球第一次到达地面时的速度大小为vB，由运动学公式有vB＝ ①‎ 将h＝0.8 m代入上式，得vB＝4 m/s. ②‎ ‎(2)设两球相碰前后，A球的速度大小分别为v1和v′1(v′1＝0)，B球的速度分别为v2和v′2.由运动学规律可得v1＝gt ③‎ 由于碰撞时间极短，重力的作用可以忽略，两球相撞前后的动量守恒，总动能保持不变．规定向下的方向为正，有 mAv1＋mBv2＝mBv′2 ④‎ mAv＋mBv＝mBv′ ⑤‎ 设B球与地面相碰后的速度大小为v′B，由运动学及碰撞的规律可得v′B＝vB ⑥‎ 设P点距地面的高度为h′，由运动学规律可得 h′＝ ⑦‎ 联立②③④⑤⑥⑦式，并代入已知条件可得 h′＝0.75 m.‎ 答案：(1)4 m/s　(2)0.75 m 7‎