高中物理数学物理法模拟试题及解析

高中物理数学物理法模拟试题及解析

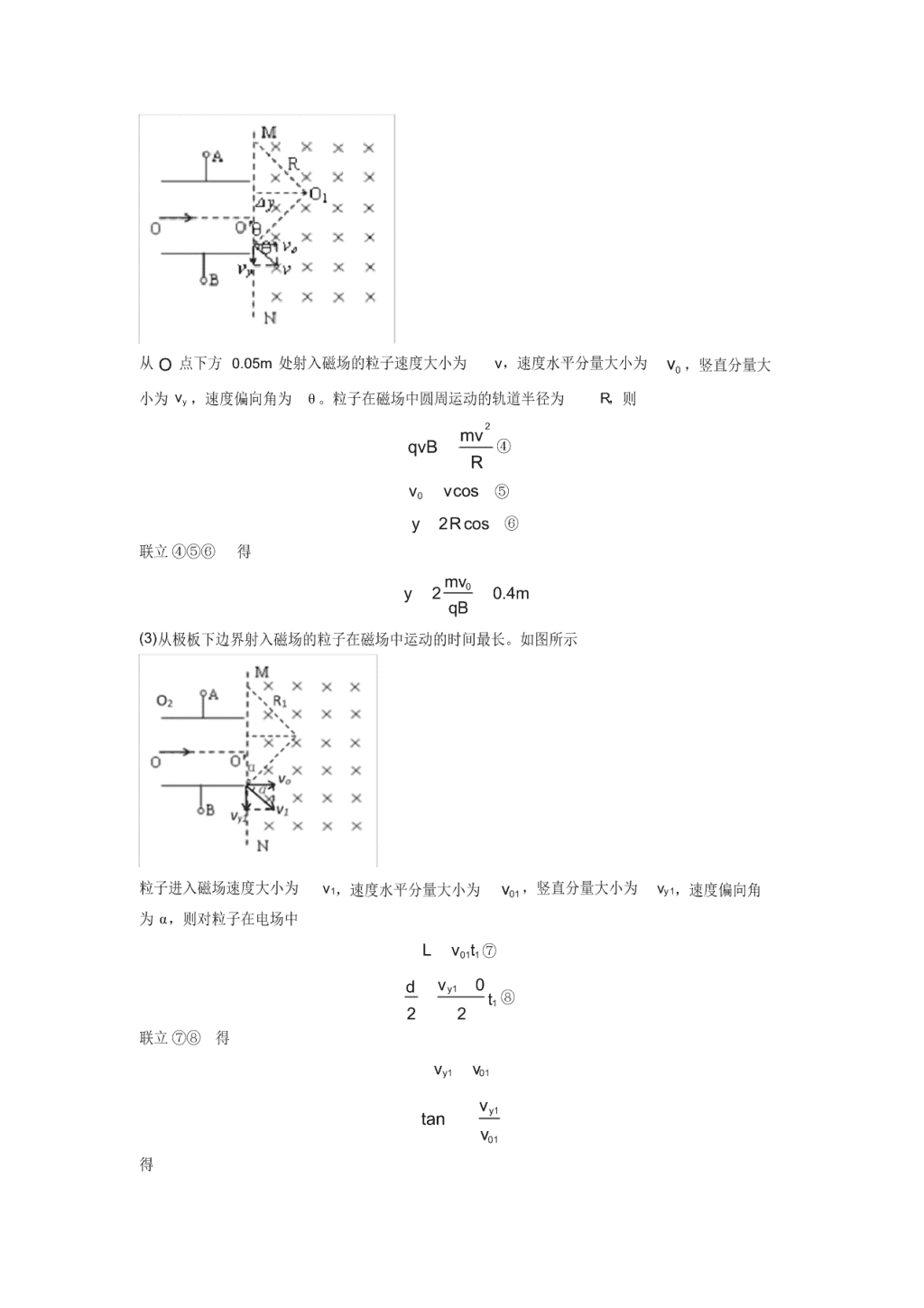
高中物理数学物理法模拟试题及解析 一、数学物理法 1．两块平行正对的水平金属板 AB，极板长 0.2mL ，板间距离 0.2md ，在金属板右 端竖直边界 MN 的右侧有一区域足够大的匀强磁场，磁感应强度 35 10 TB ，方向垂直 纸面向里。两极板间电势差 UAB 随时间变化规律如右图所示。现有带正电的粒子流以 5 0 10 m/sv 的速度沿水平中线 OO 连续射入电场中，粒子的比荷 810 C/kgq m ，重力忽 略不计，在每个粒子通过电场的极短时间内，电场视为匀强电场（两板外无电场）。求： (1)要使带电粒子射出水平金属板，两金属板间电势差 UAB 取值范围； (2)若粒子在距 O 点下方 0.05m 处射入磁场，从 MN 上某点射出磁场，此过程出射点与入 射点间的距离 y ； (3)所有粒子在磁场中运动的最长时间 t。 【答案】 (1) 100V 100VABU ；(2)0.4m ；(3) 69.42 10 s 【解析】 【分析】 【详解】 (1)带电粒子刚好穿过对应偏转电压最大为 mU ，此时粒子在电场中做类平抛运动，加速大 小为 a，时间为 t 1。水平方向上 0 1L v t ① 竖直方向上 2 1 1 2 2 d at ② 又由于 mUq ma d ③ 联立 ①②③ 得 m 100VU 由题意可知，要使带电粒子射出水平金属板，两板间电势差 100V 100VABU (2)如图所示 从 O 点下方 0.05m 处射入磁场的粒子速度大小为 v，速度水平分量大小为 0v ，竖直分量大 小为 yv ，速度偏向角为 θ。粒子在磁场中圆周运动的轨道半径为 R，则 2mvqvB R ④ 0 cosv v ⑤ 2 cosy R ⑥ 联立 ④⑤⑥ 得 02 0.4mmvy qB (3)从极板下边界射入磁场的粒子在磁场中运动的时间最长。如图所示 粒子进入磁场速度大小为 v1，速度水平分量大小为 01v ，竖直分量大小为 vy1，速度偏向角 为 α，则对粒子在电场中 01 1L v t ⑦ 1 1 0 2 2 yvd t ⑧ 联立 ⑦⑧ 得 1 01yv v 1 01 tan yv v 得 π 4 粒子在磁场中圆周运动的轨道半径为 R ，则 2 1 1 mvqv B R ⑨ 1mvR qB ⑩ 带电粒子在磁场中圆周运动的周期为 T 1 2π 2πR mT v qB ? 在磁场中运动时间 2π (π 2 ) 2π t T ? 联立 ?? 得 6 63π 10 s 9.42 10 st 2．如图所示，圆心为 O1、半径 4cmR 的圆形边界内有垂直纸面方向的匀强磁场 B1，边 界上的 P 点有一粒子源，能沿纸面同时向磁场内每个方向均匀发射比荷 62.5 10 C/kgq m 、速率 51 10 m/sv 的带负电的粒子，忽略粒子间的相互作用及重 力。其中沿竖直方向 PO1 的粒子恰能从圆周上的 C 点沿水平方向进入板间的匀强电场（忽 略边缘效应）。两平行板长 1 10cmL （厚度不计），位于圆形边界最高和最低两点的切 线方向上， C 点位于过两板左侧边缘的竖线上，上板接电源正极。距极板右侧 2 5cmL 处 有磁感应强度为 2 1TB 、垂直纸面向里的匀强磁场， EF、MN 是其左右的竖直边界（上下 无边界），两边界间距 8cmL ， O1C 的延长线与两边界的交点分别为 A 和 O2，下板板的 延长线与边界交于 D，在 AD 之间有一收集板，粒子打到板上即被吸收（不影响原有的电 场和磁场）。求： (1)磁感应强度 B1 的方向和大小； (2)为使从 C 点进入的粒子出电场后经磁场偏转能打到收集板上，两板所加电压 U 的范围； (3)当两板所加电压为 (2)中最大值时，打在收集板上的粒子数与总粒子数的比值 η。（可用 反三解函数表示，如 π 1arcsin 6 2 ） 【答案】 (1) 1 1B T，方向垂直纸面向里； (2)1280V 2400VU ； (3) 1 7arcsin arcsin 16 8 π 【解析】 【分析】 【详解】 (1)由题可知，粒子在圆形磁场区域内运动半径 r R 则 2 1 vqvB m R 得 1 1TB 方向垂直纸面向里。 (2)如图所示 211 ( ) 2 2 LqUy mR v 且要出电场 0 4cmy 在磁场 B2 中运动时 2 2 v qvB m r 合 ， cos vv a合 进入 B2 后返回到边界 EF时，进出位置间距 2 cosy r a 得 2 2mvy qB 代入得 8cmy 说明与加速电场大小无关。要打到收集板上，设粒子从 C点到 EF边界上时所发生的侧移为 y0，需满足 04cm 8cmy 且 1 10 2 2 2 L y Ly L 得 2cm 4cmy sinr r a L 且 1 2tan ya L 得 150 cm 4 y 综上需满足 152cm cm 4 y 即两板所加电压 U 满足 1280V 2400VU (3)由 (2)可知，两板间加最大电压 2400V 时，带电粒子出电场时的偏转距离为 15 4 cm，则要 打到收集板上，粒子应从 PO1 左侧的 θ角和右侧的 β角之间出射，其中 1sin 16 ， 7sin 8 即能打到收集板上的粒子数占总粒数的比值 1 7arcsin arcsin 16 8 π 3．如图所示，在 x≤0的区域内存在方向竖直向上、电场强度大小为 E的匀强电场，在 x>0 的区域内存在方向垂直纸面向外的匀强磁场。现一带正电的粒子从 x 轴上坐标为（ -2l，0） 的 A 点以速度 v0 沿 x 轴正方向进入电场，从 y 轴上坐标为（ 0，l）的 B 点进入磁场，带电 粒子在 x>0 的区域内运动一段圆弧后，从 y 轴上的 C点（未画出）离开磁场。已知磁场的 磁感应强度大小为，不计带电粒子的重力。求： (1)带电粒子的比荷； (2)C点的坐标。 【答案】 (1) 2 0 2 vq m lE ；(2)（0，-3t ） 【解析】 【详解】 (1)带电粒子在电场中做类平抛运动， x 轴方向 02l v t y 轴方向 21 2 qEl t m 联立解得 2 0 2 vq m lE (2)设带电粒子经过 B 点时的速度方向与水平方向成 θ角 0 0 tan 1y qE tv m v v 解得 45 则带电粒子经过 B 点时的速度 02v v 由洛伦兹力提供向心力得 2mvqvB r 解得 2 2mvr l qB 带电粒子在磁场中的运动轨迹如图所示 根据几何知识可知弦 BC的长度 2 4L r l 4 3l l l 故 C 点的坐标为（ 0，-3t）。 4．［选修模块 3-5］如图所示，玻璃砖的折射率 2 3 n ，一细光束从玻璃砖左端以入射 角 i 射入，光线进入玻璃砖后在上表面恰好发生全反射．求光速在玻璃砖中传播的速度 v 及入射角 i． (已知光在真空中传播速度 c=3.0 ×108 m/s，计算结果可用三角函数表示 )． 【答案】 83 3 10 / 2 v m s ； 3sin 3 i 【解析】 【分析】 【详解】 根据 cn v ， 83 3 10 / 2 v m s 全反射条件 1sin C n ，解得 C=600，r=300， 根据 sin sin in r ， 3sin 3 i 5．质量为 M 的木楔倾角为 θ (θ < 45 °)，在水平面上保持静止，当将一质量为 m 的木块放 在木楔斜面上时，它正好匀速下滑．当用与木楔斜面成 α角的力 F 拉木块，木块匀速上 升，如图所示 (已知木楔在整个过程中始终静止 )． (1)当 α＝θ时，拉力 F 有最小值，求此最小值； (2)求在 (1)的情况下木楔对水平面的摩擦力是多少？ 【答案】 （1） min sin 2F mg （2） 1 sin 4 2 mg 【解析】 【分析】 （1）对物块进行受力分析，根据共点力的平衡，利用正交分解，在沿斜面和垂直斜面两方 向列方程，进行求解． （2）采用整体法，对整体受力分析，根据共点力的平衡，利用正交分解，分解为水平和竖 直两方向列方程，进行求解． 【详解】 木块在木楔斜面上匀速向下运动时，有 mgsin mgcos＝ ，即 tan＝ (1)木块在力 F 的作用下沿斜面向上匀速运动，则： Fcos mgsin f＝ ＋ NFsin F mgcos＋ ＝ Nf F＝ 联立解得： 2mgsinF cos 则当 ＝ 时， F 有最小值 ， 2minF mgsin＝ (2)因为木块及木楔均处于平衡状态，整体受到地面的摩擦力等于 F 的水平分力，即 f Fcos 当 ＝ 时， 12 2 4 2 f mgsin cos mgsin 【点睛】 木块放在斜面上时正好匀速下滑隐含动摩擦因数的值恰好等于斜面倾角的正切值，当有外 力作用在物体上时，列平行于斜面方向的平衡方程，求出外力 F的表达式，讨论 F 取最小 值的条件． 6．如图所示，在 xOy 平面的第一、第四象限有方向垂直于纸面向里的匀强磁场；在第二 象限有一匀强电场，电场强度的方向沿 y 轴负方向。原点 O 处有一粒子源，可在 xOy 平面 内向 y 轴右侧各个方向连续发射大量速度大小在 00 ~ v 之间，质量为 m ，电荷量为 q 的 同种粒子。在 y 轴正半轴垂直于 xOy 平面放置着一块足够长的薄板，薄板上有粒子轰击的 区域的长度为 0L 。已知电场强度的大小为 2 0 0 9 4 mvE qL ，不考虑粒子间的相互作用，不计粒 子的重力。 (1)求匀强磁场磁感应强度的大小 B ； (2)在薄板上 0 2 Ly 处开一个小孔，粒子源发射的部分粒子穿过小孔进入左侧电场区域，求 粒子经过 x 轴负半轴的最远点的横坐标； (3)若仅向第四象限各个方向发射粒子： 0t 时，粒子初速度为 0v ，随着时间推移，发射 的粒子初速度逐渐减小，变为 0 2 v 时，就不再发射。不考虑粒子之间可能的碰撞，若穿过薄 板上 0 2 Ly 处的小孔进入电场的粒子排列成一条与 y 轴平行的线段，求 t 时刻从粒子源发 射的粒子初速度大小 v t 的表达式。 【答案】 (1) 0 0 2mvB qL ；(2) 0 3 3 x L ；(3) 0 0 0 π2sin( ) 6 vv v t L 或者 0 0 0 ( ) π2sin( ) 6 vv t v t L 【解析】 【详解】 (1)速度为 0v 的粒子沿 x 轴正向发射，打在薄板的最远处，其在磁场中运动的半径为 0r ，由 牛顿第二定律 2 0 0 0 mvqv B r ① 0 0 2 Lr ② 联立，解得 0 0 2mvB qL ③ (2)如图 a 所示 速度为 v 的粒子与 y 轴正向成 角射出，恰好穿过小孔，在磁场中运动时，由牛顿第二定 律 2mvqvB r ④ 而 0 4sin Lr ⑤ 粒子沿 x 轴方向的分速度 sinxv v ⑥ 联立，解得 0 2x vv ⑦ 说明能进入电场的粒子具有相同的沿 x 轴方向的分速度。当粒子以速度为 0v 从 O点射入， 可以到达 x 轴负半轴的最远处。粒子进入电场时，沿 y 轴方向的初速度为 yv ，有 2 2 0 0 3 2y xv v v v ⑧ 20 1 2 2y L qEv t t m ⑨ 最远处的横坐标 xx v t ⑩ 联立，解得 0 3 3 x L (3)要使粒子排成一排，粒子必须在同一时刻进入电场。粒子在磁场在运动轨迹如图 b 所示 周期相同，均为 0 0 π2π LmT Bq v 又 0 02sin 2 v v v v 粒子在磁场中的运动时间 2π 2 2π t T 以 0v 进入磁场的粒子，运动时间最长，满足 π 6 ，其在磁场中运动时间 m 5 6 t T 以不同速度射入的粒子，要同时到达小孔，有 mt t t 联立，解得 0 0 0 π2sin( )6 vv v tL 或者 0 0 0 ( ) π2sin( )6 vv t v tL 7．如图所示，半圆形玻璃砖的半径为 R，圆心为 O。一束单色光由玻璃砖上的 P 点垂直于 半圆底面射入玻璃砖，其折射光线射向底面的 Q 点（图中未画出），折射率为 3 ，测得 P 点与半圆底面的距离为 2 R 。计算确定 Q 点的位置。 【答案】 3 3 3 R 【解析】 【详解】 如图所示 P 点折射有 sin sin in r 由几何关系得 1cos 2 PMi R i r 解得 30 则有 QP QO 又有 3 cos 3 PMQP R 则 3 3 3 NQ R QO R 即 Q 点与玻璃砖上边缘相距 3 3 3 R 。 8．质量为 M 的木楔倾角为 θ，在水平面上保持静止，当将一质量为 m 的木块放在木楔斜 面上时，它正好匀速下滑．如果用与木楔斜面成 α角的力 F 拉着木块匀速上升，如图所示 (已知木楔在整个过程中始终静止 )． (1)当 α＝θ时，拉力 F 有最小值，求此最小值； (2)当 α＝θ时，木楔对水平面的摩擦力是多大？ 【答案】 (1)mgsin 2θ (2) 1 2 mgsin 4θ 【解析】 【分析】 【详解】 木块在木楔斜面上匀速向下运动时，有 mgsinθ＝μ mgcosθ 即 μ＝ tanθ. (1)木块在力 F 作用下沿斜面向上匀速运动，有 Fcosα＝mgsinθ＋Ff Fsinα＋FN＝mgcosθ Ff＝μFN 解得 F＝ 2 sin cos sin mg ＝ 2 sin cos cos cos sin sin mg a ＝ sin 2 cos( ) mg 则当 α＝θ时， F 有最小值，为 Fmin＝mgsin2θ. (2)因为木块及木楔均处于平衡状态，整体受到地面的摩擦力等于 F 的水平分力，即 Ff＝Fcos(α＋θ) 当 α＝ θ时， F 取最小值 mgsin 2θ， Ffm＝Fmincos2θ＝mg·sin 2θcos2θ＝ 1 2 mgsin4θ. 9．一架旧式轰炸机在 h=720m 超低空以 v0=50m/s 速度沿水平方向飞行，在其正下方与其 飞行路线平行的笔直公路上有一辆汽车在沿相同方向运动，轰炸机发现汽车时与汽车的水 平距离为 s0=800m，而此时汽车正从静止开始以 a=1m/s 2 的加速度做匀加速直线运动，汽 车速度最大只能达到 40m/s ．轰炸机在发现汽车 △t 时间后投下炸弹恰好击中汽车． g="10" m/s 2．求（ 1）炸弹从离开飞机到击中汽车，水平方向的位移为多少？（ 2）时间 △ t 为多 少？（不计空气阻力） 【答案】（ 1）600m （2）8s 【解析】 试题分析 :（1）轰炸机投下的炸弹在空中做平抛运动，时间为 t ，由 t=12s 炸弹从投下到击中汽车，水平位移为 l l= v0t 解得 l =600m （2）从发现汽车到击中汽车，炸弹在水平方向的位移为 s s= v0（△t+t） 汽车的位移为 s＇ s0+ s＇=s 解得 △t =8s 考点 :平抛运动、匀变速直线运动的规律． 【名师点睛】对平抛规律的理解及应用 10．落地速度： v＝＝，以 θ表示落地速度与 x 轴正方向间的夹角，有 tan θ＝＝，即落地 速度也只与初速度 v0 和下落高度 h 有关． 11． 在考古中为了测定古物的年代，可通过测定古物中碳 14 与碳 12 的比例，其物理过程 可简化为如图所示，碳 14 与碳 12 经电离后的原子核带电量都为 q，从容器 A 下方的小孔 S不断飘入电压为 U 的加速电场，经过 S 正下方的小孔 O 后，沿 SO方向垂直进入磁感应 强度为 B、方向垂直纸面向外的匀强磁场中，最后打在相机底片 D上并被吸收。已知 D 与 O 在同一平面内，其中碳 12 在底片 D 上的落点到 O 的距离为 x，不考虑粒子重力和粒子在 小孔 S处的初速度。 (1)求碳 12 的比荷； (2)由于粒子间存在相互作用，从 O 进入磁场的粒子在纸面内将发生不同程度的微小偏转 （粒子进入磁场速度大小的变化可忽略），其方向与竖直方向的最大偏角为 α，求碳 12 在 底片 D 上的落点到 O 的距离的范围； (3)实际上，加速电场的电压也会发生微小变化（设电压变化范围为 U±ΔU），从而导致进 入磁场的粒子的速度大小也有所不同。现从容器 A 中飘入碳 14 与碳 12 最终均能打在底片 D 上，若要使这两种粒子的落点区域不重叠，则 ΔU 应满足什么条件？（粒子进入磁场时 的速度方向与竖直方向的最大偏角仍为 α） 【答案】 (1) 2 2 8q U m B x ；(2) 距离范围为 cos ~x x ； (3) 2 2 7cos 6 7cos 6 U U 【解析】 【分析】 【详解】 (1)经加速电场有 21 2 qU mv 在磁场中 2mvqvB r 1 2 r x 解得碳 12 的比荷 2 2 8q U m B x (2)粒子在磁场中圆运动半径 2 2 qmU xr qB 由图像可知，粒子左偏 α角（轨迹圆心为 O1）或右偏 α角（轨迹圆心为 O2），落点到 O 的距离相等均为 L=2rcosθ，故 θ=0°时落点到 O 的距离最大 Lmax=2r=x 故 θ=α时落点到 O 的距离最小 Lmin=2rcosα=xcosα 所以落点到 O 的距离范围为 cos ~x x 。 (3)设碳 12 的质量为 m1，碳 14 的质量为 m2，并且 1 2 12 6 14 7 m m 根据 1 2mUr B q 可知： 碳 12 的运动半径 1 1 21 mUr B q 碳 12 的最大半径 1 1max 2 ( Δ )1 m U Ur B q 同理： 碳 14 的运动半径 2 2 21 m Ur B q 碳 14 的最小半径 2 2min 2 ( Δ )1 m U Ur B q 若要使这两种粒子的落点区域不重叠，打中底片时离 O 点的距离应需满足：碳 14 的最近 距离大于碳 12 的 最远距离，即 2r 1max 2r2mincosα 联立解得 ΔU 应满足的条件 2 2 2 1 2 2 2 1 cos 7cos 6Δ cos 7cos 6 m mU U U m m 答： (1)碳 12 的比荷为 2 2 8U B x ；(2)碳 12 在底片 D 上的落点到 O 的距离的范围为 cos ~x x ；(3)若要使这两种粒子的落点区域不重叠，则 n U 应满足 2 2 7cos 6Δ 7cos 6 U U 。 【点睛】 本题考查带电粒子在复合场中的运动，加速场运用动能定理，粒子在磁场中做匀速圆周运 动，利用洛伦兹力提供向心力结合几何关系，第三问难点在于找出粒子不重叠的条件， 即：打中底片时离 O 点的距离应需满足：碳 14 的最近距离大于碳 12 的最远距离。 12．有一个边长为 1.4mL 的正方形桌子，桌面离地高度为 1.25mh ．一个质量为 m 的小物块可从桌面中心 O 点以初速 0 2m/sv 沿着桌面任意方向运动直至落地．设动摩擦 因素为 0.2 （取 210m/sg ），求 （1）设物块在桌面滑动距离为 s ，求物块刚离开桌面时的速度 v 与 s 的关系． （2）物块在桌面滑动距离 s为多大时，物块水平运动距离最大？最大距离为多少？ （3）物块水平运动距离最大时，物块运动的总时间为多少？ 【答案】（ 1） 2 0 2v v gs （2） 3 m 4 s 5 4 m （3） 1s 【解析】 【分析】 【详解】 （1）物块在桌面滑动过程，根据动能定理可得： 2 2 0 1 1 2 2 mgs mv mv 得到： 2 0 2v v gs ； （2）离开桌子后，物块做平抛运动： 水平方向： 1s vt 竖直方向： 21 2 h gt 则物块水平运动距离为： 2 01 2 2hX s s v gs gs 代入已知条件： 1X s s 令： 1 s x，则得到： 2 1X x x 当 1 1 2 2 ( 1) 2 bx a 时， X 有最大值 则有 11 2 s ，得到 3 m 4 s 时，总的水平运动距离 X 取得最大值，最大值为： max 3 1 5 (m) 4 2 4 X ； （3）设物块在桌面运动时间为 1t ，加速度为 a ，则： mg ma ， 0 1v v at 可得物块在桌面运动时间为： 0 1 0.5sv vt g 平抛运动时间为： 2 2 0.5sht g 所以总运动时间为： 1 2 1st t t ． 13． 如图所示，位于竖直平面内的坐标系 xOy，在其第三象限空间有沿水平方向的、垂直 于纸面向外的匀强磁场，磁感应强度大小为 B＝0.5 T，还有沿 x 轴负方向的匀强电场，场 强大小为 E＝2 N/C。在其第一象限空间有沿 y 轴负方向、场强大小也为 E 的匀强电场，并 在 y>h＝ 0.4 m 的区域有磁感应强度也为 B 的垂直于纸面向里的匀强磁场。一个带电荷量为 q 的油滴从图中第三象限的 P 点得到一初速度，恰好能沿 PO 做匀速直线运动（ PO与 x 轴 负方向的夹角为 θ＝45°），并从原点 O 进入第一象限。已知重力加速度 g 取 10 m/s 2。 求： (1)油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比，并指出油滴带 何种电荷； (2)油滴在 P 点得到的初速度大小； (3)油滴在第一象限运动的时间以及油滴离开第一象限处的坐标值。 【答案】 (1)1:1: 2 ，负电； (2) 4 2 m/s ；(3)0.828 s，（ 4.0 m， 0） 【解析】 【分析】 【详解】 (1)分析油滴受力可知，要使油滴做匀速直线运动，油滴应带负电，受力如图所示： 由平衡条件和几何关系得 cos45f qE sin45 =f mg 则油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比 mg∶qE∶ f＝1:1: 2 (2)对油滴在垂直 PO方向上应用平衡条件，有 qvB＝2Eqsin 45 ° 代入数据解得 v＝ 4 2 m/s。 (3)由 (1)可知，油滴在第一象限内受到的重力等于电场力，故油滴在电场与重力场的复合场 中做匀速直线运动，在电场、磁场、重力场三者的复合场中做匀速圆周运动，轨迹如图所 示，由 O 到 A 匀速运动的位移为 s1＝ = 2 0.4 2m sin 45? h h 运动时间为 t1＝ 1s v ＝0.1s 油滴在复合场中做匀速圆周运动的周期 2πmT qB ，由几何关系知油滴由 A 到 C运动的时间 为 2 1 2π π 0.628s 4 2 2 m Et T qB Bg 从 C 到 N，粒子做匀速直线运动，由对称性知，运动时间 t3＝t1＝0.1 s 则油滴在第一象限内总的运动时间为 t＝t 1＋t 2＋t3＝0.828 s 设 OA、AC、 CN 段在 x 轴上的投影分别为 x1、x2、x3，则 x1＝x3＝h＝ 0.4 m x2＝ 2 r＝ 2 mv qB 由 (1)可知 2 mg＝qvB 代入上式可得 x2＝ 3.2 m，所以油滴在第一象限内沿 x 轴方向运动的总位移为 x＝x1＋x2＋x3＝4 m 油滴离开第一象限时的位置坐标为（ 4.0 m，0）。 答： (1)油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比为 1:1: 2 ，油滴带负电荷； (2)油滴在 P 点得到的初速度大小为 4 2 m/s；(3)油滴在第一象 限运动的时间为 0.828 s，油滴离开第一象限处的坐标值为（ 4.0 m ，0）。 14． 如图所示，正方形光滑水平台面 WXYZ边长 L=1.8m，距地面高 h=0.8m。CD线平行于 WX 边，且它们间距 d=0.1m。一个质量为 m 的微粒从 W 点静止释放，在 WXDC平台区域 受到一个从 W 点指向 C点的恒力 F1=1.25 × 10-11N 作用，进入 CDYZ平台区域后， F1 消失， 受到另一个力 F2 作用，其大小满足 F2=5× 10-13v（v 是其速度大小），运动过程中其方向总 是垂直于速度方向，从而在平台上做匀速圆周运动，然后由 XY边界离开台面，（台面以外 区域 F2=0）。微粒均视为质点，取 g=10m/s 2。 (1)若微粒质量 m=1× 10-13kg，求微粒在 CDYZ平台区域运动时的轨道半径； (2)若微粒质量 m=1× 10-13kg，求微粒落地点到平台下边线 AB 的距离。 【答案】 (1)1m；(2)1.2m 【解析】 【分析】 【详解】 (1)微粒从 W 到 C，由牛顿第二定律得 1F ma 又 2 2v ad 所以 11 1 13 2 2 1.25 10 m/s 5m/s 1 0.1 10 F dv m 微粒在 CDYZ区域运动时， 1 2 35 10 vF v k 提供向心力，由牛顿第二定律得 2vkv m r 得 13 13 1 10 m 1m 5 0 5 1 mvr k (2)微粒在 CDYZ区域运动时，其运行轨迹如图 由几何关系得 cos 0.8L r r sin 0.6 微粒离开平台后做平抛运动 21 2 h gt x vt 所以 2 2 0.85 m 2m 10 hx v g 故微粒落地点到平台下边线 AB 的距离为 sin 2 0.6m 1.2ms x 15． 图甲为一种大型游乐项目“空中飞椅”，用不计重力的钢丝绳将座椅挂在水平悬臂边 缘。设备工作时，悬臂升到离水平地面 24m 高处，以 1rad/s 的角速度匀速转动时，座椅 到竖直转轴中心线的距离为 7.5m （简化示意图乙），座椅和乘客（均视为质点）质量共 计 80kg ，钢丝绳长为 5m 。忽略空气阻力，取重力加速度 210 m/ sg 。试计算此时 (1)钢丝绳的拉力大小； (2)若游客身上的物品脱落，因惯性水平飞出直接落到地面，求落地点到竖直转轴中心线的 距离。 【答案】（ 1）1000N；（ 2）16.8m 【解析】 【分析】 【详解】 (1)设备以 1rad/ s 的角速度匀速转动时，对座椅和乘客，设细绳与竖直方向夹角为 ，水平 方向由牛顿第二定律可得 sinT ma① 竖直方向由平衡关系可得 cosT mg② 由加速度公式可得 2a r ③ 联立①②③式，代入 1rad/s、 7.5mr 、 80kgm 解得 1000NT ④ (2)游客身上惯性飞出而脱落的物品做平抛运动，水平方向匀速运动 x vt ⑤ 竖直方向做自由落实体运动 21 2 y gt ⑥ 由线速度公式可知 v r ⑦ 由几何关系可得 24 5cosy ⑧ 2 2 2R x r ⑨ 联立②④⑤⑥⑦⑧⑨式，解得落地点到竖直转轴中心线的距离 7.5 5 m 16.8mR ⑩