2018届二轮复习　带电粒子在有界磁场中运动的临界问题的解题技巧课件(共59张）

2018届二轮复习　带电粒子在有界磁场中运动的临界问题的解题技巧课件(共59张）

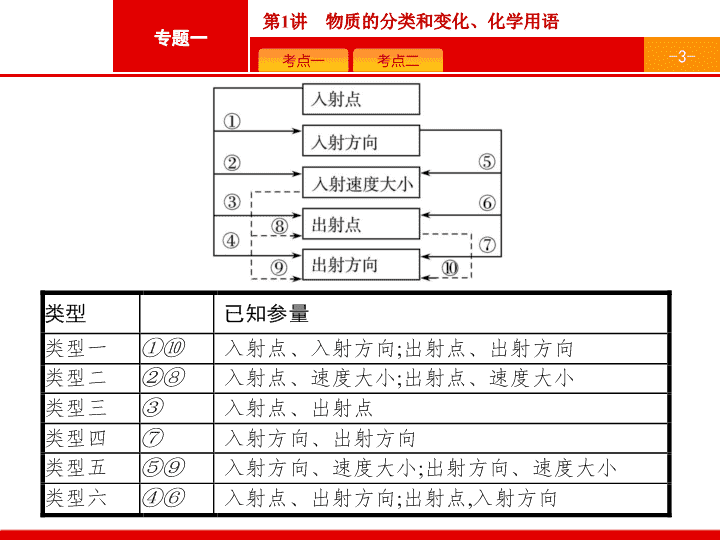
微专题三　带电粒子在有界磁场中运动的临界问题的解题技巧 - 2 - 带电粒子 ( 质量 m 、电荷量 q 确定 ) 在有界磁场中运动时 , 涉及的可能变化的参量有入射点、入射速度大小、入射方向、出射点、出射方向、磁感应强度大小、磁场方向等 , 其中磁感应强度大小与入射速度大小影响的都是轨道半径的大小 , 可归并为同一因素 ( 以 “ 入射速度大小 ” 代表 ), 磁场方向在一般问题中不改变 , 若改变 , 也只需将已讨论情况按反方向偏转再分析一下即可。 在具体问题中 , 这五个参量一般都是已知两个 , 剩下其他参量不确定 ( 但知道变化范围 ) 或待定 , 按已知参量可将问题分为如下 10 类 , 并可归并为 6 大类型。 - 3 - - 4 - 所有这些问题 , 其通用解法是 : 第一步 , 找准轨迹圆圆心可能的位置 ; 第二步 , 按一定顺序尽可能多地作不同圆心对应的轨迹圆 ( 一般至少画 5 个轨迹圆 ); 第三步 , 根据所作的图和题设条件 , 找出临界轨迹圆 , 从而抓住解题的关键点。 - 5 - 已知入射点和入射速度方向 , 但入射速度大小不确定 ( 即轨道半径不确定 ) 这类问题的特点是 : 所有轨迹圆圆心均在过入射点、垂直入射速度的同一条直线上。 - 6 - 【例 1 】 如图所示 , 长为 L 的水平极板间有垂直于纸面向内的匀强磁场 , 磁感应强度为 B , 板间距离也为 L , 极板不带电。现有质量为 m 、电荷量为 q 的带正电粒子 ( 不计重力 ), 从左边极板间中点处垂直磁感线以速度 v 水平射入磁场 , 欲使粒子不打在极板上 , 可采用的办法是 ( 　　 ) - 7 - 分析 : 粒子初速度方向已知 , 故不同速度大小的粒子轨迹圆圆心均在垂直初速度的直线上 ( 如图甲 ), 在该直线上取不同点为圆心 , 半径由小取到大 , 作出一系列圆 ( 如图乙 ), 其中轨迹圆 ① 和 ② 为临界轨迹圆。轨道半径小于轨迹圆 ① 或大于轨迹圆 ② 的粒子 , 均可射出磁场而不打在极板上 。 - 8 - 答案 : AB 解析 : 粒子擦着上板从右边穿出时 , 圆心在 O 点 , - 9 - 易错提醒 容易漏选 A, 错在没有将 r 先取较小值再连续增大 , 从而未 分析出 粒子还可以从磁场左边界穿出的情况。 - 10 - 练 1 　 两平面荧光屏互相垂直放置 , 分别取两屏所在直线为 x 轴和 y 轴 , 交点 O 为原点 , 如图所示。在 y> 0,0 0, x>a 的区域有垂直于纸面向外的匀强磁场 , 两区域内的磁感应强度大小均为 B 。在 O 点处有一小孔 , 一束质量为 m 、电荷量为 q ( q> 0) 的粒子沿 x 轴经小孔射入磁场 , 最后打在竖直和水平荧光屏上 , 使荧光屏发亮。入射粒子的速度可取从零到某一最大值之间的各种数值。已知速度最大的 粒子 在 0 a 的 区 域中 运动的时间之比为 2 ∶ 5, 在磁场中 运动 的 总时间 为 , 其中 T 为该粒子在磁感应 强 度 为 B 的匀强磁场中做圆周运动的周期 。 试 求两个荧光屏上亮线的范围 ( 不计重力 的 影响 ) 。   - 11 - 分析 : 粒子在 0 a 的区域 , 由对称性可知 , 粒子在 x>a 的区域内的轨迹圆圆心均在 x= 2 a 的直线上 , 在 x= 2 a 的直线上取不同点为圆心 , 半径由小取到大 , 可作出一系列圆 ( 如图乙 ), 其中轨迹圆 ③ 为半径最小的情况 , 轨迹圆 ② 为题目所要求的速度最大的粒子的轨迹。 - 12 - - 13 - 速度小的粒子将在 xa 的区域中运动的时间 , 由题意可知 - 15 - 【易错提醒】 本题容易把握不住隐含条件 —— 所有在 x>a 的区域内的轨迹圆圆心均在 x= 2 a 直线上 , 从而造成在 x>a 的区域内的作图困难 ; 另一方面 , 在 x>a 的区域内作轨迹圆时 , 半径未从轨迹圆 ③ 半径开始取值 , 致使轨迹圆 ③ 未作出 , 从而将水平荧光屏发亮范围的左边界坐标确定为 x=a 。 - 16 - 已知入射点和入射速度大小 ( 即轨道半径大小 ), 但入射速度方向不确定 这类问题的特点是 : 所有轨迹圆的圆心均在一个 “ 圆心圆 ” 上 —— 所谓 “ 圆心圆 ”, 是指以入射点为圆心 , 以 r = 为 半径的圆。 - 17 - 【例 2 】 如图所示 , 在 0 ≤ x ≤ a 、 0 ≤ y ≤ 范围 内有垂直于 xOy 平面向外的匀强磁场 , 磁感应强度大小为 B 。坐标原点 O 处有一个粒子源 , 在某时刻发射大量质量为 m 、电荷量为 q 的带正电粒子 , 它们的速度大小相同 , 速度方向均在 xOy 平面内 , 与 y 轴正方向的夹角分布在 0 ~ 90 ° 范围内。己知粒子在磁场中做圆周运动的半径 介于 到 a 之间 , 从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的 ( 不计重力及粒子间的相互作用 ) ( 1) 速度的大小 ; (2) 速度方向与 y 轴正方向夹角的正弦。 - 18 - 分析 : 本题给定的情形是粒子轨道半径 r 大小确定但初速度方向不确定 , 所有粒子的轨迹圆都要经过入射点 O , 入射点 O 到任一圆心的距离均为 r , 故所有轨迹圆的圆心均在一个 “ 圆心圆 ”—— 以入射点 O 为圆心、 r 为半径的圆周上 ( 如图甲 ) 。考虑到粒子是向右偏转 , 我们从最左边的轨迹圆画起 —— 取 “ 圆心圆 ” 上不同点为圆心、 r 为半径作出一系列圆 , 如图乙所示 ; 其中 , 轨迹 ① 对应弦长大于轨迹 ② 对应弦长 —— 半径一定、圆心角都较小时 ( 均小于 180 ° ), 弦长越长 , 圆心角越大 , 粒子在磁场中运动时间越长 —— 故轨迹 ① 对应圆心角应为 90 ° 。 - 19 - - 20 - 解析 : 设粒子的发射速度为 v , 粒子做圆周运动的轨道半径为 R , - 21 - 易错提醒 由于作图不仔细而把握不住 “ 轨迹 ① 对应弦长大于轨迹 ② 对应弦长 —— 半径一定、圆心角都较小时 ( 均小于 180 ° ), 弦长越长 , 圆心角越大 , 粒子在磁场中运动时间越长 ”, 从而误认为轨迹 ② 对应粒子在磁场中运动时间最长。这类题作图要讲一个小技巧 —— 按粒子偏转方向移动圆心作图。 - 22 - 练 2 　 如图所示 , 在正方形区域 abcd 内充满方向垂直纸面向里的、磁感应强度为 B 的匀强磁场。在 t= 0 时刻 , 一位于 ad 边中点 O 的粒子源在 abcd 平面内发射出大量的同种带电粒子 , 所有粒子的初速度大小相同 , 方向与 Od 边的夹角分布在 0 ~ 180 ° 范围内。已知沿 Od 方向发射的粒子在 t=t 0 时刻刚好从磁场边界 cd 上的 P 点离开磁场 , 粒子在磁场中做圆周运动的半径恰好等于正方形边长 L , 粒子重力不计 , 求 :   - 23 - (2) 假设粒子源发射的粒子在 0 ~ 180 ° 范围内均匀分布 , t 0 时刻仍在磁场中的粒子数与粒子源发射的总粒子数之比 ; (3) 从粒子发射到全部粒子离开磁场所用的时间。 【分析】 以 L 为半径、 O 点为圆心作 “ 圆心圆 ”( 如图甲 ); 由于粒子逆时针偏转 , 从最下面的轨迹开始画起 ( 轨迹 ① ), 在 “ 圆心圆 ” 上取不同点为圆心、以 L 为半径作出一系列圆 ( 如图乙 ); 其中轨迹 ① 与轨迹 ④ 对称 , 在磁场中运动时间相同 ; 轨迹 ② 并不经过 c 点 , 轨迹 ② 对应弦长短于轨迹 ③ 对应弦长 —— 即沿轨迹 ③ 运动的粒子最后离开磁场。 - 24 - - 25 - 解析 : (1) 初速度沿 Od 方向发射的粒子在磁场中运动的轨迹如图 , 其圆心为 N , 由几何关系有 粒子做圆周运动的向心力由洛仑兹力提供 , 根据牛顿第二定律得 - 26 - (2) 依题意 , 同一时刻仍在磁场中的粒子到 O 点距离相等。在 t 0 时刻仍在磁场中的粒子应位于以 O 点为圆心 , OP 为半径的弧 PW 上。 (3) 在磁场中运动时间最长的粒子的轨迹应该与磁场边界 b 点相交 , 设此粒子运动轨迹对应的圆心角为 θ , - 27 - 【易错提醒】 本题因作图不认真易错误地认为轨迹 ② 经过 c 点 , 认为轨迹 ② 对应弦长等于轨迹 ③ 对应弦长 , 于是将轨迹 ② 对应粒子作为在磁场中运动时间最长的粒子进行计算 ; 虽然计算出来结果正确 , 但依据错误。 - 28 - 已知入射点和出射点 , 但未知初速度大小 ( 即未知半径大小 ) 和方向 这类问题的特点是 : 所有轨迹圆圆心均在入射点和出射点连线的中垂线上。 - 29 - 【例 3 】 如图所示 , 无重力空间中有一恒定的匀强磁场 , 磁感应强度的方向垂直于 xOy 平面向外 , 大小为 B , 沿 x 轴放置一个垂直于 xOy 平面的较大的荧光屏 , P 点位于荧光屏上 , 在 y 轴上的 A 点放置一放射源 , 可以不断地沿平面内的不同方向以大小不等的速度放射出质量为 m 、电荷量为 +q 的同种粒子 , 这些粒子打到荧光屏上能在屏上形成一条亮线 , P 点处在亮线上 , 已知 OA=OP=l , 求 : ( 1) 若能打到 P 点 , 则粒子速度的最小值为多少 ? (2) 若能打到 P 点 , 则粒子在磁场中运动的最长时间为多少 ? - 30 - 分析 : 粒子既经过 A 点又经过 P 点 , 因此 AP 连线为粒子轨迹圆的一条弦 , 圆心必在该弦的中垂线 OM 上 ( 如图甲 ) 。在 OM 上取不同点为圆心、以圆心和 A 点连线长度为半径由小到大作出一系列圆 ( 如图乙 ), 其中轨迹 ① 对应半径最小 , 而轨迹 ② 对应粒子是轨道半径最大的 , 由图可知其对应圆心角也最大。 - 31 - 解析 : (1) 粒子在磁场中运动 , 洛伦兹力提供向心力 , 设粒子的速度大小为 v 时 , 其在磁场中的运动半径为 R , 则由牛顿第二定律有 qBv=m 若粒子以最小的速度到达 P 点时 , 其轨迹一定是以 AP 为直径的圆 ( 如图中圆 O 1 所示 ) - 32 - - 33 - 练 3 　 图中虚线 MN 是一垂直纸面的平面与纸面的交线。在平面右侧的半空间存在一磁感强度为 B 的匀强磁场 , 方向垂直纸面向外 , O 是 MN 上的一点 , 从 O 点可以向磁场区域发射电荷量为 +q , 质量为 m , 速率为 v 的粒子 , 粒子射入磁场时的速度可在纸面内各个方向 , 已知先后射入的两个粒子恰好在磁场中给定的 P 点相遇。 P 点到 O 点的距离为 L , 不计重力及粒子间的相互作用。   - 34 - (1) 求所考查的粒子在磁场中的轨道半径。 (2) 求这两个粒子从 O 点射入磁场的时间间隔。 分析 : 如图甲 , 作 OP 连线中垂线 , 然后在中垂线上取关于 C 对称的两点 O 1 、 O 2 为圆心 , 过 O 、 P 作出两个轨迹圆 ①② , 如图乙所示。保留相遇前轨迹如图丙所示。 - 35 - 解析 : (1) 设粒子在磁场中做圆周运动的轨道半径为 R , (2) 如图所示 , 以 OP 为弦可以画两个半径相同的圆 , 分别表示在 P 点相遇的两个粒子的轨迹。圆心分别为 O 1 、 O 2 , 过 O 点的直径分别为 OO 1 Q 1 、 OO 2 Q 2 , 在 O 点处两个圆的切线分别表示两个粒子的射入方向 , 用 θ 表示它们之间的夹角。由几何关系可知 , ∠ PO 1 Q 1 = ∠ PO 2 Q 2 = θ , 从 O 点射入到相遇 , 粒子 1 的路程为半个圆周加弧长 Q 1 P=R θ , 粒子 2 的路程为半个圆周减弧长 PQ 2 =R θ , 粒子 1 的 - 36 - - 37 - 已知初、末速度的方向 ( 所在直线 ), 但未知初速度大小 ( 即未知轨道半径大小 ) 这类问题的特点是 : 所有轨迹圆的圆心均在初、末速度延长线形成的角的角平分线上。 - 38 - 【例 4 】 在 xOy 平面上的某圆形区域内 , 存在一垂直纸面向里的匀强磁场 , 磁感应强度大小为 B 。一个质量为 m 、电荷量为 +q 的带电粒子 , 由原点 O 开始沿 x 轴正方向运动 , 进入该磁场区域后又射出该磁场 ; 后来 , 粒子经过 y 轴上的 P 点 , 此时速度方向与 y 轴的夹角为 30 ° ( 如图所示 ), 已知 P 到 O 的距离为 L , 不计重力的影响 。 (1) 若磁场区域的大小可根据需要而改变 , 试求粒子速度的最大可能值 ; (2) 若粒子速度大小为 v = , 试求该圆形磁场区域的最小面积。 - 39 - 分析 : 初、末速度所在直线必定与粒子的轨迹圆相切 , 轨迹圆圆心到两条直线的距离 ( 即轨道半径 ) 相等 , 因此 , 圆心必位于初、末速度延长线形成的角的角平分线 QC 上 ( 如图甲 ); 在角平分线 QC 上取不同的点为圆心 , 由小到大作出一系列轨迹圆 ( 如图乙 ), 其中以 C 点为圆心的轨迹 ① 是可能的轨迹圆中半径最大的 , 其对应的粒子速度也最大。 甲 　　　　　　　　　 乙 - 40 - 解析 : 过 P 点作末速度所在直线 , 交 x 轴于 Q 点 , 经分析可知 , 粒子在磁场中做圆周运动的轨迹的圆心必在 ∠ OQP 的角平分线 QC 上 , 如图甲所示。设粒子在磁场中作匀速圆周运动的轨道半径为 r , 则由牛顿第二定律 , 由此可知粒子速度越大 , 其轨道半径越大 , 由图乙可知 , 速度最大的粒子在磁场中运动轨迹的圆心是 y 轴上的 C 点。 (1) 如图丙所示 , 速度最大时粒子的轨迹圆过 O 点、且与 PQ 相切于 A 点。 - 41 - 　　　　 丙 　　　　　　　　　　　 丁 - 42 - - 43 - 练 4 　 如图所示 , xOy 平面内存在着沿 y 轴正方向的匀强电场。一个质量为 m , 电荷量为 +q 的粒子从坐标原点 O 以速度 v 0 沿 x 轴正方向开始运动。当它经过图中虚线上的 M (2 a , a ) 点时 , 撤去电场 , 粒子继续运动一段时间后进入一个矩形匀强磁场区域 ( 图中未画出 ), 又从虚线上的某一位置 N 处沿 y 轴负方向运动并再次经过 M 点。已知磁场方向垂直 xOy 平面 ( 纸面 ) 向里 , 磁感应强度大小为 B , 不计粒子的重力 , 试求 :   - 44 - (1) 电场强度的大小 ; (2) N 点的坐标 ; (3) 矩形磁场的最小面积 。 【分析】 粒子在电场中偏转后进入 MN 右侧 , 初速度方向已知 , 另一方面 , 粒子末速度由 N 指向 M 。初速度、末速度所在直线交于点 M , 过 M 点作 ∠ NMP 角平分线 MO' , 粒子轨迹圆的圆心必在直线 MO' 上。取其上一点 O' 为圆心作出轨迹圆 ( 如图所示 ) 。 - 45 - 解析 : (1) 粒子从 O 到 M 做类平抛运动 , 设时间为 t , 粒子从 P 点进入磁场 , 从 N 点离开磁场 , 粒子在磁场中以 O' 点为圆心做匀速圆周运动 , 设半径为 R , - 46 - (3) 当矩形磁场为图示虚线矩形时的面积最小。则矩形的两个边长分别为 - 47 - 已知初速度的大小 ( 即已知轨道半径大小 ) 和方向 , 但入射点不确定 这类问题的特点是 : 所有轨迹圆的圆心均在将入射点组成的边界沿垂直入射速度方向平移一个半径距离的曲线上。 - 48 - 【例 5 】 如图所示 , 长方形 abcd 的长 ad= 0 . 6 m, 宽 ab= 0 . 3 m, O 、 e 分别是 ad 、 bc 的中点 , 以 e 为圆心、 eb 为半径的圆弧和以 O 为圆心、 Od 为半径的圆弧组成的区域内有垂直纸面向里的匀强磁场 ( eb 边界上无磁场 ) 磁感应强度 B= 0 . 25 T 。一群不计重力、质量 m= 3 × 10 - 7 kg 、电荷量 q=+ 2 × 10 - 3 C 的带正电粒子以速度 v= 5 × 10 2 m/s 沿垂直 ad 方向且垂直于磁场方向射入磁场区域 , 则下列判断正确的是 ( 　　 ) A. 从 Od 边射入的粒子 , 出射点全部分布在 Oa 边 B. 从 aO 边射入的粒子 , 出射点全部分布在 ab 边 C. 从 Od 边射入的粒子 , 出射点分布在 ab 边 D. 从 ad 边射人的粒子 , 出射点全部通过 b 点 - 49 - 答案 : D 的轨迹 ( 圆心在 O 点 ), ② 为从 O 点射入粒子的轨迹 ( 圆心在 a 点 ), ③ 为从 a 点射入粒子的轨迹 , 从 d 、 O 之间入射粒子在磁场中转 过 圆周 后沿 eb 边界做直线运动最终汇聚于 b 点 , 从 O 、 a 之间入射粒子先做直线运动再进入磁场做圆周运动 , 由作图易知这些粒子也汇聚于 b 点。 - 50 - - 51 - 练 5 　 如图所示 , 在 xOy 平面内有一半径为 R 、与 x 轴相切于原点的圆形区域 , 该区域内有垂直于 xOy 平面的匀强磁场。在圆的左边 0 0) 和初速度 v 的带电微粒沿 x 轴正方向射向该区域 , 其中沿半径 AO' 方向进入磁场区域的带电微粒经磁场偏转后 , 从坐标原点 O 沿 y 轴负方向离开。 ( 不计重力及粒子间的相互作用 )   - 52 - (1) 求磁感应强度 B 的大小和方向。 (2) 请指出这束带电微粒与 x 轴相交的区域 , 并说明理由。 - 53 - - 54 - 已知初速度方向 ( 所在直线 ) 和出射点 , 但入射点不确定 这类问题的特点是 : 所有轨迹圆的圆心均在 “ 以初速度所在直线为准线、出射点为焦点的抛物线 ” 上。 - 55 - 【例 6 】 如图所示 , 现有一质量为 m 、电荷量为 e 的电子从 y 轴上的 P (0, a ) 点以初速度 v 0 ( 大小可调 ) 平行于 x 轴射出 , 在 y 轴右侧某一圆形区域加一垂直于 xOy 平面向里的匀强磁场 , 磁感应强度大小为 B ( 大小可调 ) 。为了使电子能从 x 轴上的 Q ( b ,0) 点射出磁场。试求满足条件的磁场的最小面积 , 并求出该磁场圆圆心的坐标。 - 56 - 解析 : 本题中 , 电子初速度所在直线已知 , 电子进入磁场的入射点在该直线上 , 则可知电子在磁场中做圆周运动的轨迹圆与该直线相切、且经过 Q 点 , 所以电子轨迹圆圆心到该直线和到 Q 点的距离相等 , 即电子轨迹圆圆心在以该直线为准线、 Q 点为焦点的抛物线上。 在该抛物线上从左向右取不同点为圆心 , 做出一系列轨迹圆 , 可以看出所有这些轨迹中轨迹 ① 所需圆形磁场的直径最小。此时 磁 - 57 - 练 6 　 电子质量为 m , 电荷量为 e , 从坐标原点 O 处沿 xOy 平面射入第一象限 , 射入时速度方向不同 , 速度大小均为 v 0 , 如图所示。现在某一区域加一方向向外且垂直于 xOy 平面的匀强磁场 , 磁感应强度为 B , 若这些电子穿过磁场后都能垂直射到荧光屏 MN 上 , 荧光屏与 y 轴平行 , 求 :   (1) 电子从 y 轴穿过的范围 ; (2) 荧光屏上光斑的长度 ; (3) 所加磁场范围的最小面积。 - 58 - 解析 : (1) 设电子在磁场中运动的半径为 R , 由牛顿第二定律 得 - 59 - (2) 如图所示 , 求光斑长度 , 关键是找到两个边界点 , 初速度方向沿 x 轴正方向的电子 , 沿弧 OB 运动到 P ; 初速度方向沿 y 轴正方向的电子 , 沿弧 OC 运动到 Q (3) 沿任一方向射入第一象限的电子经磁场偏转后都能垂直打到荧光屏 MN 上 , 所加最小面积的磁场的边界是以 O' (0, R ) 为圆心 , R 为半径的圆的一部分 , 如图中实线所示 , 所以磁场范围的最小面积为