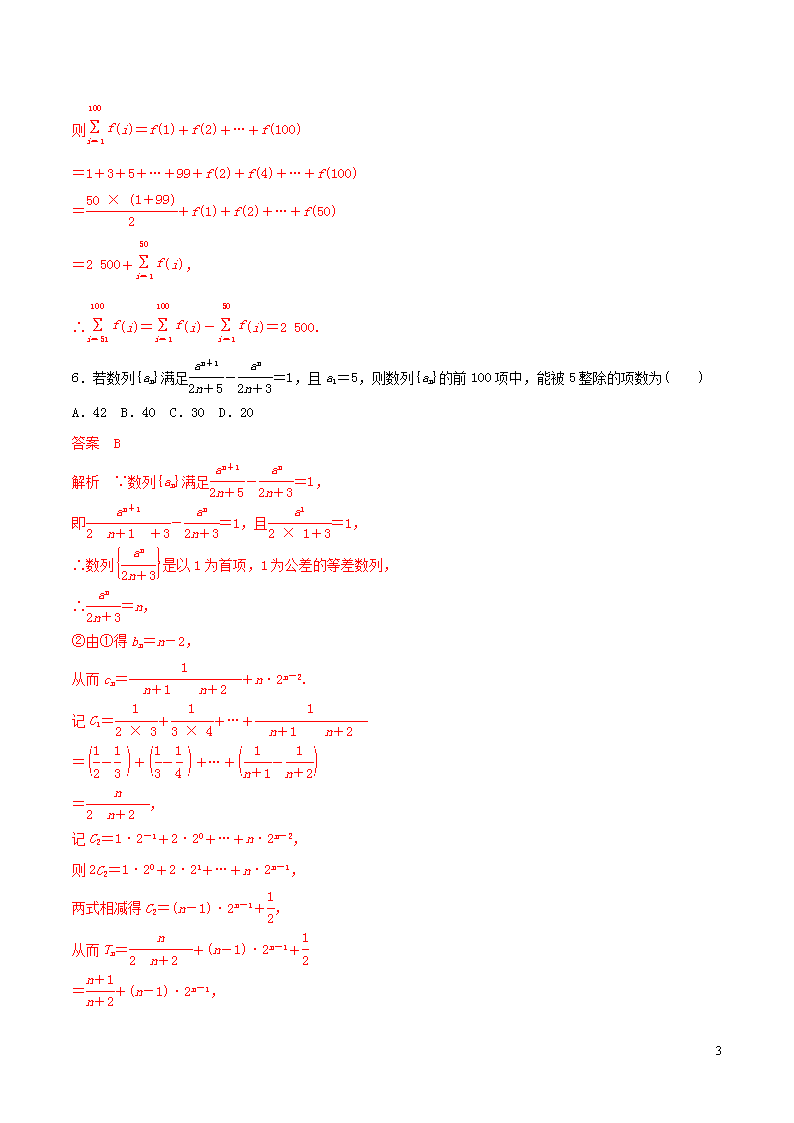2019年高考数学考纲解读与热点难点突破专题12数列的综合问题(热点难点突破)文(含解析)
数列的综合问题
1.删去正整数数列1,2,3,… 中的所有完全平方数,得到一个新数列,这个数列的第2 018项是( )
A.2 062 B.2 063
C.2 064 D.2 065
答案 B
解析 由题意可得,这些数可以写为12,2,3,22,5,6,7,8,32,…,第k个平方数与第k+1个平方数之间有2k个正整数,而数列12,2,3,22,5,6,7,8,32,…,452共有2 025项,去掉45个平方数后,还剩余2 025-45=1 980(个)数,所以去掉平方数后第2 018项应在2 025后的第38个数,即是原来数列的第2 063项,即为2 063.
2.已知数列{an}满足0
10的n的最小值为( )
A.60 B.61 C.121 D.122
答案 B
解析 由a-8a+4=0,得a+=8,
所以a+=8+8(n-1)=8n,
所以2=a++4=8n+4,
所以an+=2,
即a-2an+2=0,
所以an==±,
因为010得>11,
所以n>60.
3.已知数列{an}满足a1=1,an+1-an≥2(n∈N*),Sn为数列{an}的前n项和,则( )
A.an≥2n+1 B.Sn≥n2
C.an≥2n-1 D.Sn≥2n-1
答案 B
5
解析 由题意得a2-a1≥2,a3-a2≥2,a4-a3≥2,…,
an-an-1≥2,
∴a2-a1+a3-a2+a4-a3+…+an-an-1≥2(n-1),
∴an-a1≥2(n-1),∴an≥2n-1.
∴a1≥1,a2≥3,a3≥5,…,an≥2n-1,
∴a1+a2+a3+…+an≥1+3+5+…+2n-1,
∴Sn≥(1+2n-1)=n2.
4.数列{an}满足a1=,an=(n∈N*),若对n∈N*,都有k>++…+成立,则最小的整数k是( )
A.3 B.4 C.5 D.6
答案 C
5.已知f(n)表示正整数n的所有因数中最大的奇数,例如:12的因数有1,2,3,4,6,12,则f(12)=3;21的因数有1,3,7,21,则f(21)=21,那么(i)的值为( )
A.2 488 B.2 495 C.2 498 D.2 500
答案 D
解析 由f(n)的定义知f(n)=f(2n),且若n 为奇数则f(n)=n,
5
则(i)=f(1)+f(2)+…+f(100)
=1+3+5+…+99+f(2)+f(4)+…+f(100)
=+f(1)+f(2)+…+f(50)
=2 500+(i),
∴(i)=(i)-(i)=2 500.
6.若数列{an}满足-=1,且a1=5,则数列{an}的前100项中,能被5整除的项数为( )
A.42 B.40 C.30 D.20
答案 B
解析 ∵数列{an}满足-=1,
即-=1,且=1,
∴数列是以1为首项,1为公差的等差数列,
∴=n,
②由①得bn=n-2,
从而cn=+n·2n-2.
记C1=++…+
=++…+
=,
记C2=1·2-1+2·20+…+n·2n-2,
则2C2=1·20+2·21+…+n·2n-1,
两式相减得C2=(n-1)·2n-1+,
从而Tn=+(n-1)·2n-1+
=+(n-1)·2n-1,
则不等式Tn0,因为n∈N*且n≠1,故n>9,
5
从而最小正整数n的值是10.
14.已知数列{an}的前n项和为Sn,且满足Sn-n=2(an-2)(n∈N*).
(1)证明:数列{an-1}为等比数列;
(2)若bn=an·log2(an-1),数列{bn}的前n项和为Tn,求Tn.
(1)证明 ∵Sn-n=2(an-2),
当n≥2时,Sn-1-(n-1)=2(an-1-2),
两式相减,得an-1=2an-2an-1,
∴an=2an-1-1,∴an-1=2(an-1-1),
∴=2(n≥2)(常数).
又当n=1时,a1-1=2(a1-2),
得a1=3,a1-1=2,
∴数列{an-1}是以2为首项,2为公比的等比数列.
(2)解 由(1)知,an-1=2×2n-1=2n,
∴an=2n+1,
又bn=an·log2(an-1),
∴bn=n(2n+1),
∴Tn=b1+b2+b3+…+bn
=(1×2+2×22+3×23+…+n×2n)+(1+2+3+…+n),
设An=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,
则2An=1×22+2×23+…+(n-1)×2n+n×2n+1,
两式相减,得
-An=2+22+23+…+2n-n×2n+1
=-n×2n+1,
∴An=(n-1)×2n+1+2.
又1+2+3+…+n=,
∴Tn=(n-1)×2n+1+2+(n∈N*).
5
5