不确定关系教案

不确定关系教案

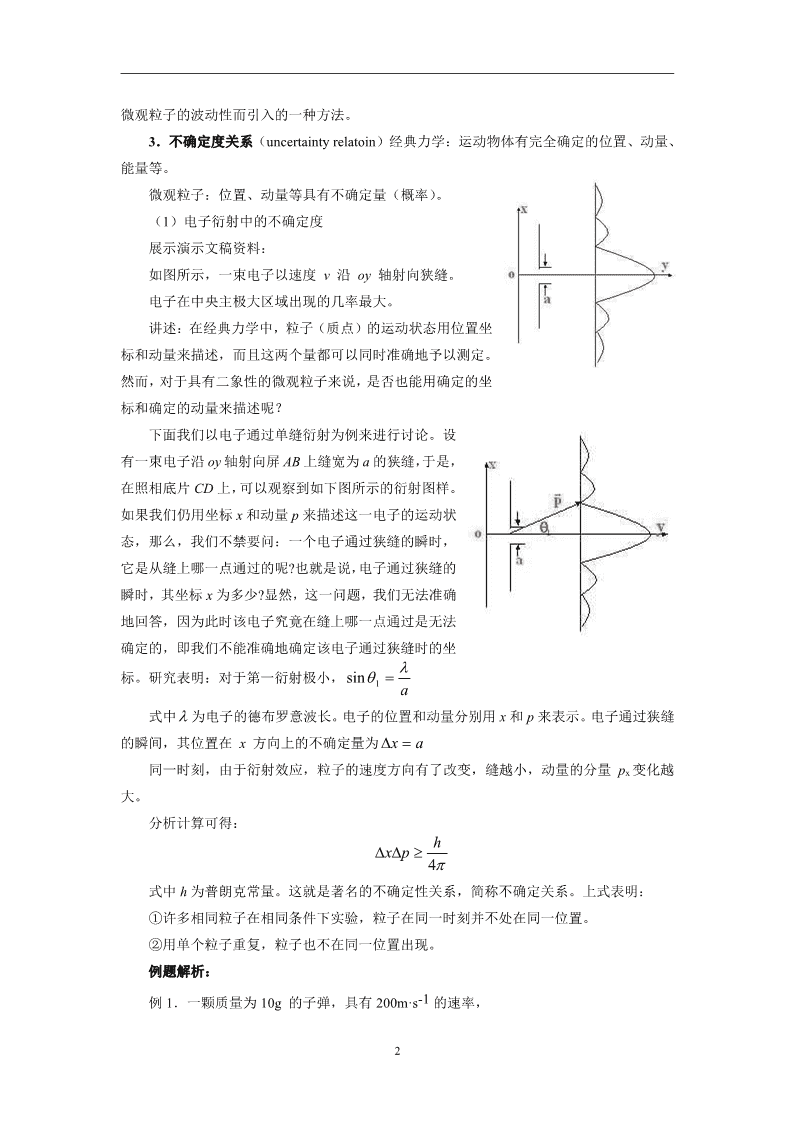
‎ ‎ ‎17.5 不确定关系 ‎★新课标要求 ‎（一）知识与技能 ‎1．了解不确定关系的概念和相关计算．‎ ‎2．了解物理模型与物理现象 ‎（二）过程与方法 经历科学探究过程，认识科学探究的意义，尝试应用科学探究的方法研究物理问题，验证物理规律。‎ ‎（三）情感、态度与价值观 能领略自然界的奇妙与和谐，发展对科学的好奇心与求知欲，乐于探究自然界的奥秘，能体验探索自然规律的艰辛与喜悦。‎ ‎★教学重点 不确定关系的概念 ‎ ‎★教学难点 对不确定关系的定量应用 ‎★教学方法 教师启发、引导，学生讨论、交流。‎ ‎★教学用具： 投影片，多媒体辅助教学设备 ‎★课时安排 1 课时 ‎ ‎★教学过程 ‎（一）引入新课 提问：对光的本性的认识？‎ 学生思考、回答：光具有波动性和粒子性，是一种概率波。‎ 设疑：既然光是粒子，那么它的运动还遵守牛顿运动定律吗？还能用质点的位置和动量来描述它的运动吗？‎ 点评：引发学生的好奇心，激发学习的兴趣。‎ 教师：回答是否定的。光子的运动具有不确定性。这节课我们就来学习有关知识。‎ ‎（二）进行新课 ‎1．德布罗意波的统计解释 ‎1926年，德国物理学玻恩 （Born ， 1882--1972） 提出了概率波，认为个别微观粒子在何处出现有一定的偶然性，但是大量粒子在空间何处出现的空间分布却服从一定的统计规律。‎ 展示演示文稿资料：玻恩 点评：应用物理学家的历史资料，不仅有真实感，增强了说服力，同时也能对学生进行发放教育，有利于培养学生的科学态度和科学精神，激发学生的探索精神。‎ ‎2．经典波动与德布罗意波（物质波）的区别 讲述：经典的波动（如机械波、电磁波等）是可以测出的、实际存在于空间的一种波动。而德布罗意波（物质波）‎ 4‎ ‎ ‎ 是一种概率波。简单的说，是为了描述微观粒子的波动性而引入的一种方法。‎ ‎3．不确定度关系（uncertainty relatoin）‎ 经典力学：运动物体有完全确定的位置、动量、能量等。‎ 微观粒子：位置、动量等具有不确定量（概率）。‎ ‎（1）电子衍射中的不确定度 展示演示文稿资料：‎ 如图所示，一束电子以速度 v 沿 oy 轴射向狭缝。‎ 电子在中央主极大区域出现的几率最大。‎ 讲述：在经典力学中，粒子（质点）的运动状态用位置坐标和动量来描述，而且这两个量都可以同时准确地予以测定。然而，对于具有二象性的微观粒子来说，是否也能用确定的坐标和确定的动量来描述呢？‎ 下面我们以电子通过单缝衍射为例来进行讨论。‎ 设有一束电子沿oy轴射向屏AB上缝宽为a的狭缝，于是，在照相底片CD上，可以观察到如下图所示的衍射图样。如果我们仍用坐标x和动量p来描述这一电子的运动状态，那么，我们不禁要问：一个电子通过狭缝的瞬时，它是从缝上哪一点通过的呢?也就是说，电子通过狭缝的瞬时，其坐标x为多少?显然，这一问题，我们无法准确地回答，因为此时该电子究竟在缝上哪一点通过是无法确定的，即我们不能准确地确定该电子通过狭缝时的坐标。‎ 研究表明：‎ 对于第一衍射极小，‎ 式中为电子的德布罗意波长。‎ 电子的位置和动量分别用x和p来表示。‎ 电子通过狭缝的瞬间，其位置在 x 方向上的不确定量为 同一时刻，由于衍射效应，粒子的速度方向有了改变，缝越小，动量的分量 px变化越大。‎ 分析计算可得：‎ 式中h为普朗克常量。这就是著名的不确定性关系，简称不确定关系。‎ 上式表明：‎ ‎①许多相同粒子在相同条件下实验，粒子在同一时刻并不处在同一位置。‎ ‎②用单个粒子重复，粒子也不在同一位置出现。‎ 例题解析：‎ 4‎ ‎ ‎ 例1．一颗质量为10g 的子弹，具有200m·s-1的速率，‎ 若其动量的不确定范围为动量的0. 01%(这在宏观范围是十分精确的了)，则该子弹位置的不确定量范围为多大?‎ 解：子弹的动量 动量的不确定范围 由不确定关系式，得子弹位置的不确定范围 我们知道，原子核的数量级为10-15m，所以，子弹位置的不确定范围是微不足道的。可见子弹的动量和位置都能精确地确定，不确定关系对宏观物体来说没有实际意义。 ‎ 例2．一电子具有200 m/s的速率，动量的不确定 范围为动量的0.01%(这已经足够精确了)，则该电子的位置不确定范围有多大?‎ 解 : 电子的动量为 动量的不确定范围 由不确定关系式，得电子位置的不确定范围 我们知道原子大小的数量级为10-10m，电子则更小。在这种情况下，电子位置的不确定范围比原子的大小还要大几亿倍，可见企图精确地确定电子的位置和动量已是没有实际意义。 ‎ ‎4．微观粒子和宏观物体的特性对比 宏观物体 微观粒子 具有确定的坐标和动量，可用牛顿力学描述。‎ 没有确定的坐标和动量，需用量子力学描述。‎ 有连续可测的运动轨道，可追踪各个物体的运动轨迹。‎ 有概率分布特性，不可能分辨出各个粒子的轨迹。‎ 体系能量可以为任意的、连续变化的数值。‎ 能量量子化 。‎ 不确定度关系无实际意义 遵循不确定度关系 ‎5．不确定关系的物理意义和微观本质 ‎（1）物理意义：‎ 微观粒子不可能同时具有确定的位置和动量。粒子位置的不确定量越小，动量的不确定量就越大，反之亦然。‎ ‎（2） 微观本质：‎ 4‎ ‎ ‎ 是微观粒子的波粒二象性及粒子空间分布遵从统计规律的必然结果。‎ 不确定关系式表明：‎ ‎① 微观粒子的坐标测得愈准确() ，动量就愈不准确() ；‎ 微观粒子的动量测得愈准确() ，坐标就愈不准确() 。‎ 但这里要注意，不确定关系不是说微观粒子的坐标测不准；也不是说微观粒子的动量测不准；更不是说微观粒子的坐标和动量都测不准；而是说微观粒子的坐标和动量不能同时测准。‎ ‎② 为什么微观粒子的坐标和动量不能同时测准?‎ 这是因为微观粒子的坐标和动量本来就不同时具有确定量。这本质上是微观粒子具有波粒二象性的必然反映。‎ 由以上讨论可知，不确定关系是自然界的一条客观规律，不是测量技术和主观能力的问题。‎ ‎③ 不确定关系提供了一个判据：‎ 当不确定关系施加的限制可以忽略时，则可以用经典理论来研究粒子的运动。‎ 当不确定关系施加的限制不可以忽略时，那只能用量子力学理论来处理问题。‎ ‎（三）课堂小结 教师活动：让学生概括总结本节的内容。请一个同学到黑板上总结，其他同学在笔记本上总结，然后请同学评价黑板上的小结内容。‎ 学生活动：认真总结概括本节内容，并把自己这节课的体会写下来、比较黑板上的小结和自己的小结，看谁的更好，好在什么地方。‎ 点评：总结课堂内容，培养学生概括总结能力。‎ 教师要放开，让学生自己总结所学内容，允许内容的顺序不同，从而构建他们自己的知识框架。‎ ‎（四）作业：“问题与练习”1～4题。 ‎ ‎★教学体会 思维方法是解决问题的灵魂，是物理教学的根本；亲自实践参与知识的发现过程是培养学生能力的关键，离开了思维方法和实践活动，物理教学就成了无源之水、无本之木。学生素质的培养就成了镜中花，水中月。‎ 4‎