【物理】2020届一轮复习人教版能量守恒与可持续发展课时作业
2020届一轮复习人教版 能量守恒与可持续发展 课时作业
一、选择题(本题共10小题,每题5分,共50分)
1.(2018·课标全国Ⅱ)取水平地面为重力势能零点,一物块从某一高度水平抛出,在抛出点其动能与重力势能恰好相等。不计空气阻力。该物块落地时的速度方向与水平方向的夹角为( )
A. B. C. D.
解析:设物块抛出的初速度为v0,落地时速度为v,根据题意知,物块抛出时的机械能为m,由机械能守恒定律,mmv2,得物块落地时的速度v=v0,故物块落地时速度方向与水平方向的夹角为,选项B正确。
答案:B
2.(2018·重庆理综)某车以相同的功率在两种不同的水平路面上行驶,受到的阻力分别为车重的k1和k2倍,最大速率分别为v1和v2,则( )
A.v2=k1v1 B.v2=v1
C.v2=v1 D.v2=k2v1
解析:根据机车的起动规律可知,当牵引力等于阻力时,车速最大,有vm=,又f=kmg,则,B项正确。
答案:B
3.(2018·课标全国Ⅱ)一物体静止在粗糙水平地面上,现用一大小为F1的水平拉力拉动物体,经过一段时间后其速度变为v。若将水平拉力的大小改为F2,物体从静止开始经过同样的时间后速度变为2v。对于上述两个过程,用WF1、WF2分别表示拉力F1、F2所做的功,Wf1、Wf2分别表示前后两次克服摩擦力所做的功,则( )
A.WF2>4WF1,Wf2>2Wf1 B.WF2>4WF1,Wf2=2Wf1
C.WF2<4WF1,Wf2=2Wf1 D.WF2<4WF1,Wf2<2Wf1
解析:由v=at可知,a2=2a1;由x=at2可知,x2=2x1;根据题意,物体受的摩擦力f不变,由Wf=fx可知,Wf2=2Wf1;由a=可知,F2<2F1。由WF=Fx可知,WF2<4WF1,选项C正确。
答案:C
4.(2018·广东理综)如图是安装在列车车厢之间的摩擦缓冲器结构图。图中①和②为楔块,③和④为垫板,楔块与弹簧盒、垫板间均有摩擦。在车厢相互撞击使弹簧压缩的过程中( )
A.缓冲器的机械能守恒
B.摩擦力做功消耗机械能
C.垫板的动能全部转化为内能
D.弹簧的弹性势能全部转化为动能
解析:在弹簧压缩过程中,摩擦力做功,缓冲器的机械能不守恒,A项错误,B项正确;根据能量守恒可知,垫板的动能转化为弹簧的弹性势能以及克服摩擦力做功产生的内能,C、D两项错误。
答案:B
5.(2018·福建理综)如图,两根相同的轻质弹簧,沿足够长的光滑斜面放置,下端固定在斜面底部挡板上,斜面固定不动。质量不同、形状相同的两物块分别置于两弹簧上端。现用外力作用在物块上,使两弹簧具有相同的压缩量,若撤去外力后,两物块由静止沿斜面向上弹出并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块( )
A.最大速度相同
B.最大加速度相同
C.上升的最大高度不同
D.重力势能的变化量不同
解析:当物块达最大速度时,有mgsinθ=kx,由机械能守恒定律得Ep=mgxsinθ+,由上两式可知两物块的最大速度vmax不同,选项A错误;刚撤去F时有最大加速度amax=,所以两物块的最大加速度amax不同,选项B错误;由Ep=mghmax可知上升的最大高度不同,选项C正确;从撤去外力到物块速度第一次为零时,弹性势能全部转化为重力势能,因此重力势能变化量相同,选项D错误。
答案:C
6.
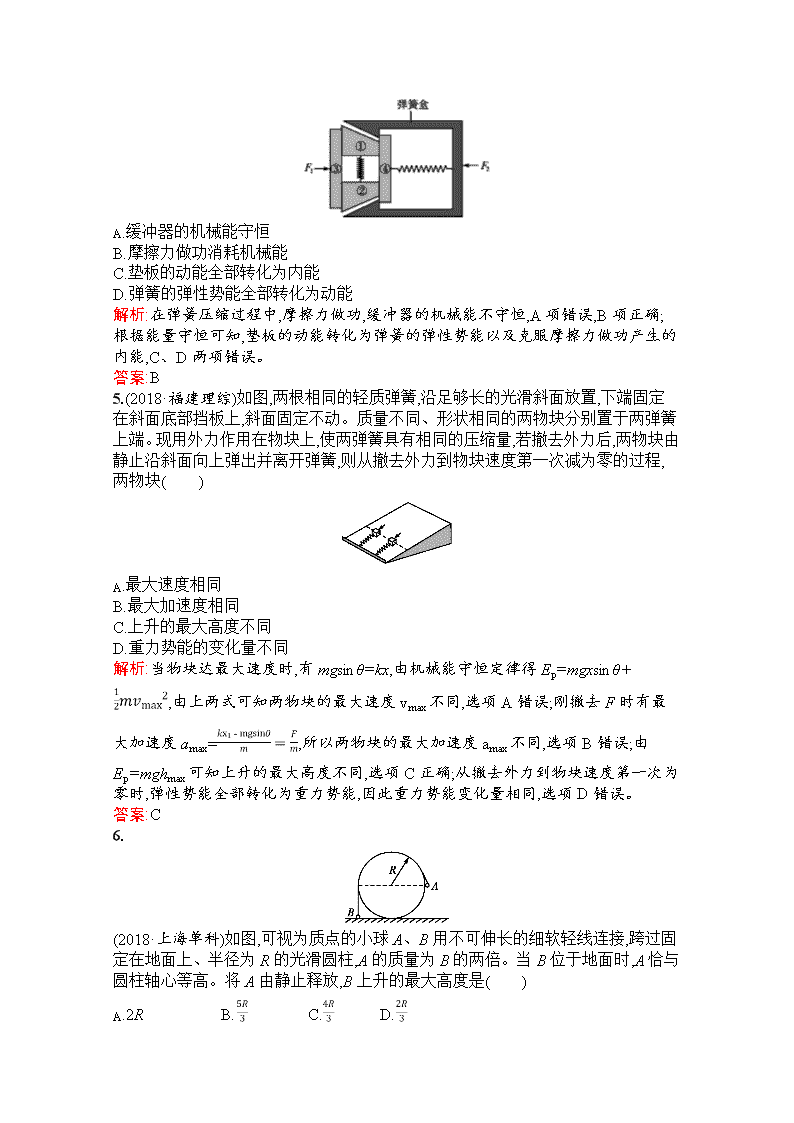
(2018·上海单科)如图,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上、半径为R的光滑圆柱,A的质量为B的两倍。当B位于地面时,A恰与圆柱轴心等高。将A由静止释放,B上升的最大高度是( )
A.2R B. C. D.
解析:设A球刚落地时两球速度大小为v,根据机械能守恒定律:2mgR-mgR=(2m+m)v2得v2=gR,B球继续上升的高度h=,B球上升的最大高度为h+R=R。
答案:C
7.
(2018·山东理综)2018年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程。某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球。设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月。以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=,其中G为引力常量,M为月球质量。若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
A.(h+2R) B.(h+R)
C.(h+R) D.(h+R)
解析:从开始发射到对接完成,“玉兔”重力势能增加量为ΔEp=;又mg月=。解得ΔEp=。“玉兔”在对接轨道上的速度为v,则由万有引力定律及向心力公式得G=m,所以v=;其动能为Ek=mv2=;对“玉兔”做的功等于其机械能增加量为W=ΔEp+ΔEk=(h+R)。故选项D正确。
答案:D
8.(多选)(2018·广东理综)游乐场中,从高处A到水面B处有两条长度相同的光滑轨道。甲、乙两小孩沿不同轨道同时从A处自由滑向B处,下列说法正确的有( )
A.甲的切向加速度始终比乙的大
B.甲、乙在同一高度的速度大小相等
C.甲、乙在同一时刻总能到达同一高度
D.甲比乙先到达B处
解析:切向加速度a=gsin θ,开始甲大于乙后来甲小于乙,选项A错误;由机械能守恒可知,甲、乙在同一高度的速度大小相等,选项B
正确;画出甲、乙的速率图像如图所示,由于两种情况路程相同(即图像与t轴所围的图形的面积相同),最后的速率相同,由图可知甲比乙先到达B处,同一时刻,甲的位置总低于乙,选项C错,D对。
答案:BD
9.(多选)(2018·江苏单科)如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连。弹簧处于自然长度时物块位于O点(图中未标出)。物块的质量为m,AB=a,物块与桌面间的动摩擦因数为μ。现用水平向右的力将物块从O点拉至A点,拉力做的功为W。撤去拉力后物块由静止向左运动,经O点到达B点时速度为零。重力加速度为g。则上述过程中( )
A.物块在A点时,弹簧的弹性势能等于W-μmga
B.物块在B点时,弹簧的弹性势能小于W-μmga
C.经O点时,物块的动能小于W-μmga
D.物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能
解析:因桌面粗糙,分析物块的运动可知,xOA>xOB,则xOA>,xOB<。把物块从O点拉到A点的过程中,根据功能关系有W=EpA+μmgxOA>EpA+μmga,则EpA
m)的滑块,通过不可伸长的轻绳跨过定滑轮连接,轻绳与斜面平行。两滑块由静止释放后,沿斜面做匀加速运动。若不计滑轮的质量和摩擦,在两滑块沿斜面运动的过程中( )
A.两滑块组成系统的机械能守恒
B.重力对M做的功等于M动能的增加
C.轻绳对m做的功等于m机械能的增加
D.两滑块组成系统的机械能损失等于M克服摩擦力做的功
解析:M在滑动时除重力做功外,还要克服摩擦力及绳的拉力做功,这三个功的代数和才等于M动能的增加,选项B错误;轻绳对m做的功用来增加m的动能及重力势能,选项C正确;两滑块组成的系统在运动过程中,由于M要克服摩擦力做功,故机械能不守恒,损失的机械能等于M克服摩擦力做的功,选项A错误,D正确。
答案:CD
二、填空题(本题共2小题,每小题8分,共16分)
11.(2018·课标全国Ⅱ)某同学利用下述装置对轻质弹簧的弹性势能进行探究:一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连;弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示。向左推小球,使弹簧压缩一段距离后由静止释放;小球离开桌面后落到水平地面。通过测量和计算,可求得弹簧被压缩后的弹性势能。
图(a)
回答下列问题:
(1)本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等。已知重力加速度大小为g。为求得Ek,至少需要测量下列物理量中的 (填正确答案标号)。
A.小球的质量m
B.小球抛出点到落地点的水平距离s
C.桌面到地面的高度h
D.弹簧的压缩量Δx
E.弹簧原长l0
(2)用所选取的测量量和已知量表示Ek,得Ek= 。
图(b)
(3)图(b)中的直线是实验测量得到的sΔx图线。从理论上可推出,如果h不变,m增加,sΔx图线的斜率会 (选填“增大”“减小”或“不变”);如果m不变,h增加,sΔx图线的斜率会 (选填“增大”“减小”或“不变”)。由图(b)中给出的直线关系和Ek的表达式可知,Ep与Δx的 次方成正比。
解析:(1)由平抛运动规律得,h=gt2,s=vt,解得,小球抛出时的速度v=s,则小球抛出时的动能Ek=mv2=,所以需要测量的物理量是小球的质量m、小球抛出点到落地点的水平距离s、桌面到地面的高度h,A、B、C三项正确。
(2)由(1)可知,Ek=。
(3)如果h不变,m增加,那么小球平抛运动的时间不变,当Δx为某一值时,小球获得的初速度减小,做平抛运动的水平位移减小,图线的斜率会减小;如果m不变,h增加,那么当Δx为某一值时,小球获得的初速度不变,小球平抛运动的时间增加,做平抛运动的水平位移增加,图线的斜率会增大;根据机械能守恒可得,Ep=Ek=,即Ep与s2成正比,又因为s与Δx成正比,所以Ep与Δx的二次方成正比。
答案:(1)ABC (2) (3)减小 增大 二
12.(2018·海南单科)现要通过实验验证机械能守恒定律。实验装置如图1所示:水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连;遮光片两条长边与导轨垂直;导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t。用d表示A点到导轨底端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A、B两点间的距离,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度。用g表示重力加速度。完成下列填空和作图:
图1
(1)若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为 ,动能的增加量可表示为 。若在运动过程中机械能守恒,与s的关系式为= 。
(2)多次改变光电门的位置,每次均令滑块自同一点(A点)下滑,测量相应的s与t值。结果如下表所示:
1
2
3
4
5
s/m
0.600
0.800
1.000
1.200
1.400
t/ms
8.22
7.17
6.44
5.85
5.43
×104 s-2
1.48
1.95
2.41
2.92
3.39
以s为横坐标,为纵坐标,在对应图2位置的坐标纸中描出第1和第5个数据点;根据5个数据点作直线,求得该直线的斜率k= ×104m-1·s-2(保留三位有效数字)。
图2
由测得的h、d、b、M和m数值可以计算出s直线的斜率k0,将k和k0进行比较,若其差值在实验允许的范围内,则可认为此实验验证了机械能守恒定律。
解析:(1)滑块的重力势能减小Mg·s·,砝码的重力势能增加mg·s,故系统的重力势能的减小量为Mg·s·-mg·s=(M-m)gs。滑块通过B点时的瞬时速度v=,系统动能的增加量为(M+m)v2=(M+m)。若在运动过程中机械能守恒,则有(M-m)gs=(M+m),则s。
(2)第1和第5个数据点及所作直线见下图。
直线的斜率约为k=2.36×104m-1·s-2。
答案:(1)(M-m)gs (M+m)s
(2)作图见解析 2.36(2.32~2.40均正确)
三、计算题(本题共3小题,共34分。解题时要有必要的步骤和文字说明)
13.(10分)(2018·福建理综)如图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切。点A距水面的高度为H,圆弧轨道BC的半径为R,圆心O恰在水面。一质量为m的游客(视为质点)可从轨道AB的任意位置滑下,不计空气阻力。
(1)若游客从A点由静止开始滑下,到B点时沿切线方向滑离轨道落在水面D点,OD=2R,求游客滑到B点时的速度vB大小及运动过程轨道摩擦力对其所做的功Wf;
(2)若游客从AB段某处滑下,恰好停在B点,又因受到微小扰动,继续沿圆弧轨道滑到P点后滑离轨道,求P点离水面的高度h。(提示:在圆周运动过程中任一点,质点所受的向心力与其速率的关系为F向=m)
解析:(1)游客从B点做平抛运动,有
2R=vBt①
R=gt2②
由①②式得
vB=③
从A到B,根据动能定理,有
mg(H-R)+Wf=-0④
由③④式得
Wf=-(mgH-2mgR)⑤
(2)设OP与OB间夹角为θ,游客在P点时的速度为vP,受到的支持力为N,从B到P由机械能守恒定律,有
mg(R-Rcosθ)=-0⑥
过P点时,根据向心力公式,有
mgcosθ-N=m⑦
N=0⑧
cosθ=⑨
由⑥⑦⑧⑨式解得
h=R⑩
答案:(1) -(mgH-2mgR) (2)R
14.(12分)(2018·北京理综)蹦床比赛分成预备运动和比赛动作两个阶段。最初,运动员静止站在蹦床上;在预备运动阶段,他经过若干次蹦跳,逐渐增加上升高度,最终达到完成比赛动作所需的高度;此后,进入比赛动作阶段。
把蹦床简化为一个竖直放置的轻弹簧,弹力大小F=kx(x为床面下沉的距离,k为常量)。质量m=50kg的运动员静止站在蹦床上,床面下沉x0=0.10m
;在预备运动中,假定运动员所做的总功W全部用于增加其机械能;在比赛动作中,把该运动员视作质点,其每次离开床面做竖直上抛运动的腾空时间均为Δt=2.0s,设运动员每次落下使床面压缩的最大深度均为x1。重力加速度g取10m/s2,忽略空气阻力的影响。
(1)求常量k,并在图中画出弹力F随x变化的示意图;
(2)求在比赛动作中,运动员离开床面后上升的最大高度hm;
(3)借助Fx图像可以确定弹力做功的规律,在此基础上,求x1和W的值。
解析:(1)床面下沉x0=0.10m时,运动员受力平衡,mg=kx0
得k==5.0×103N/m
Fx图线示意图如图所示
(2)运动员从x=0处离开床面,开始腾空,其上升、下落时间相等
hm=g()2=5.0 m
(3)参考由速度—时间图像求位移的方法,Fx图线与坐标轴所围的面积等于弹力做的功,从x1处到x=0,弹力做功WT
WT=·x1·kx1=
运动员从x1处上升到最大高度hm的过程,根据动能定理,有
-mg(x1+hm)=0
解得x1≈1.1m
对整个预备运动,由题设条件以及功和能的关系,有
W+=mg(hm+x0)
得W=2525J≈2.5×103J
答案:(1)5.0×103N/m 见解析图
(2)5.0m
(3)1.1m 2.5×103J
15.(12分)(2018·浙江理综)山谷中有三块石头和一根不可伸长的轻质青藤,其示意图如下。图中A、B、C、D均为石头的边缘点,O为青藤的固定点,h1=1.8m,h2=4.0m,x1=4.8 m,x2=8.0m。开始时,质量分别为M=10kg和m=2 kg的大、小两只滇金丝猴分别位于左边和中间的石头上,当大猴发现小猴将受到伤害时,迅速从左边石头的A点水平跳至中间石头。大猴抱起小猴跑到C点,抓住青藤下端,荡到右边石头上的D点,此时速度恰好为零。运动过程中猴子均可看成质点,空气阻力不计,重力加速度g取10m/s2。求:
(1)大猴从A点水平跳离时速度的最小值;
(2)猴子抓住青藤荡起时的速度大小;
(3)猴子荡起时,青藤对猴子的拉力大小。
解析:(1)设猴子从A点水平跳离时速度的最小值为vmin,根据平抛运动规律,有
h1=gt2①
x1=vmint②
联立①②式,得
vmin=8 m/s③
(2)猴子抓住青藤后的运动过程中机械能守恒,设荡起时速度为vC,有
(M+m)gh2=(M+m)④
vC=m/s≈9m/s⑤
(3)设拉力为T,青藤的长度为L,对最低点,由牛顿第二定律得
T-(M+m)g=(M+m)⑥
由几何关系
(L-h2)2+=L2⑦
得:L=10m⑧
综合⑤⑥⑧式并代入数据解得:T=(M+m)g+(M+m)=216N
答案:(1)8m/s (2)9m/s (3)216N