2020-2021上海上海交通大学附属第二中学高中必修三数学上期中模拟试题含答案

2020-2021上海上海交通大学附属第二中学高中必修三数学上期中模拟试题含答案

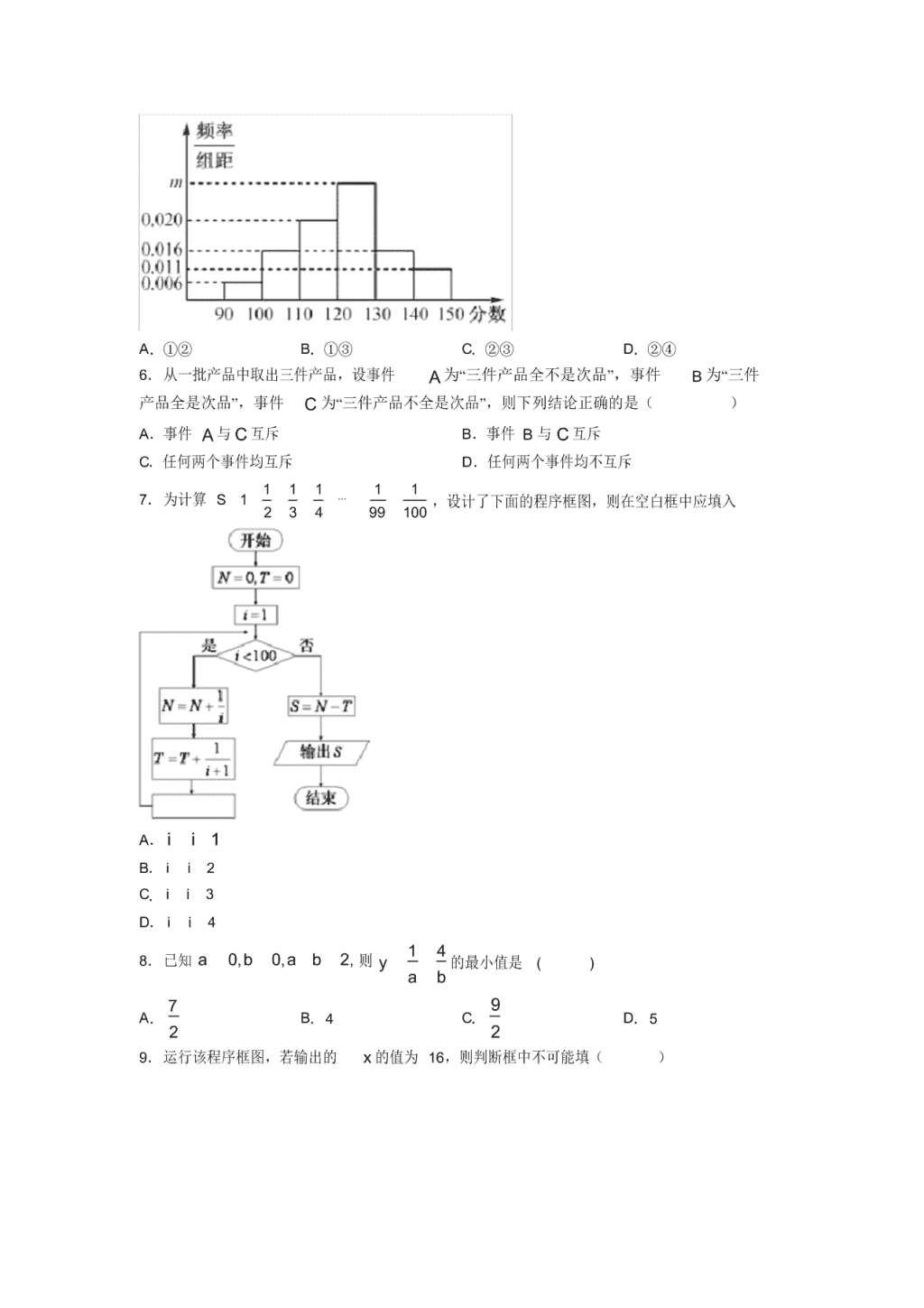
2020-2021 上海上海交通大学附属第二中学高中必修三数学上期中模拟试题含 答案 一、选择题 1．某学校为了解 1 000 名新生的身体素质，将这些学生编号为 1， 2，⋯， 1 000，从这些 新生中用系统抽样方法等距抽取 100 名学生进行体质测验，若 46 号学生被抽到，则下面 4 名学生中被抽到的是 A．8 号学生 B．200 号学生 C．616 号学生 D．815 号学生 2．民间有一种五巧板拼图游戏 . 这种五巧板（图 1）可以说是七巧板的变形，它是由一个 正方形分割而成（图 2），若在图 2 所示的正方形中任取一点，则该点取自标号为③和④ 的巧板的概率为（ ） A． 5 18 B． 1 3 C． 7 18 D． 4 9 3．甲、乙两人各写一张贺年卡随意送给丙、丁两人中的一人，则甲、乙将贺年卡都送给丁 的概率为（ ） A． 1 2 B． 1 3 C． 1 4 D． 1 5 4．设 a 是甲抛掷一枚骰子得到的点数，则方程 2 2 0x ax 有两个不相等的实数根的概 率为（ ） A． 2 3 B． 1 3 C． 1 2 D． 5 12 5．统计某校 n 名学生的某次数学同步练习成绩，根据成绩分数依次分成六组： 90,100 , 100,110 , 110,120 , 120,130 , 130,140 , 140,150 ，得到频率分布直方图 如图所示，若不低于 140 分的人数为 110. ① 0.031m ；② 800n ；③100 分以下的人数 为 60；④分数在区间 120,140 的人数占大半．则说法正确的是（ ） A．①② B．①③ C．②③ D．②④ 6．从一批产品中取出三件产品，设事件 A 为“三件产品全不是次品”，事件 B 为“三件 产品全是次品”，事件 C 为“三件产品不全是次品”，则下列结论正确的是（ ） A．事件 A 与 C 互斥 B．事件 B 与 C 互斥 C．任何两个事件均互斥 D．任何两个事件均不互斥 7．为计算 1 1 1 1 11 2 3 4 99 100 S ⋯ ，设计了下面的程序框图，则在空白框中应填入 A． 1i i B． 2i i C． 3i i D． 4i i 8．已知 0, 0, 2,a b a b 则 1 4y a b 的最小值是 ( ) A． 7 2 B．4 C． 9 2 D．5 9．运行该程序框图，若输出的 x 的值为 16，则判断框中不可能填（ ） A． 5k B． 4k C． 9k D． 7k 10． 若框图所给的程序运行结果为 ，那么判断框中应填入的关于 k 的条件是 A． ？ B． ？ C． ？ D． ？ 11． 某高校大一新生中 , 来自东部地区的学生有 2400 人、中部地区学生有 1600 人、西部地 区学生有 1000 人. 从中选取 100 人作样本调研饮食习惯 , 为保证调研结果相对准确 , 下列判 断正确的有（ ） ①用分层抽样的方法分别抽取东部地区学生 48 人、中部地区学生 32 人、西部地区学生 20 人； ②用简单随机抽样的方法从新生中选出 100 人； ③西部地区学生小刘被选中的概率为 1 50 ； ④中部地区学生小张被选中的概率为 1 5000 A．①④ B．①③ C．②④ D．②③ 12． 为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区 5 户家庭，得到 如下统计数据表： 收入 x （万 元） 8.2 8.6 10.0 11.3 11.9 支出 y （万 元） 6.2 7.5 8.0 8.5 9.8 根据上表可得回归直线方程 ?? ?y bx a ，其中 ? ??0.76,b a y bx ，据此估计，该社区一 户收入为 15 万元家庭年支出为（ ） A．11.4 万元 B．11.8 万元 C．12.0 万元 D．12.2 万元 二、填空题 13． 执行如图所示的程序框图，则输出的 m 的值为 ____. 14． 某中学采用系统抽样方法，从该校高一年级全体 800 名学生中抽 50 名学生做牙齿健康 检查．现将 800 名学生从 1 到 800 进行编号．已知从 33～48 这 16 个数中取的数是 39，则 在第 1 小组 1～16 中随机抽到的数是 ______. 15． 将一枚骰子连续掷两次，点数之积为奇数的概率为 __________． 16． 从分别写有 1，2，3，4，5 的 5 张卡片中随机抽取 1 张，放回后再随机抽取 1 张，则 抽得的第一张卡片上的数大于第二张卡片上的数的概率为 ___________． 17． 某校连续 5 天对同学们穿校服的情况进行统计，没有穿校服的人数用茎叶图表示，如 图，若该组数据的平均数为 18，则 x =_____________. 18． 如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”．执 行该程序框图，若输入的 a，b 分别为 98、63，则输出的 a =_______． 19． 为了对某课题进行研究，用分层抽样方法从三所高校 , ,A B C 的相关人员中，抽取若干 人组成研究小组，有关数据见表（单位：人） 若从高校 ,B C 抽取的人中选 2 人作专题发言，则这 2 人都来自高校 C 的概率 P __________． 20． 为了调查某班学生做数学题的基本能力，随机抽查部分学生某次做一份满分为 100 分 的数学试题，他们所得分数的分组区间为 45,55 ， 55,65 ， 65,75 ， 75,85 ， 85,95 ，由此得到频率分布直方图如下图，则这些学生的平均分为 __________. 三、解答题 21． 中国神舟十一号载人飞船在酒泉卫星发射中心成功发射，引起全国轰动．开学后，某 校高二年级班主任对该班进行了一次调查，发现全班 60 名同学中，对此事关注的占 1 3 ，他 们在本学期期末考试中的物理成绩如下面的频率分布直方图： （1）求“对此事关注”的同学的物理期末平均分（以各区间的中点代表该区间的均值）． （2）若物理成绩不低于 80 分的为优秀，请以是否优秀为分类变量， ①补充下面的 2 2 列联表： 物理成绩优秀 物理成绩不优秀 合计 对此事关注 对此事不关注 合计 ②是否有 95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系？ 参考公式： 2 2 ( ) ( )( )( )( ) n ad bck a b c d a c b d ，其中 n a b c d . 参考数据： 2 0( )P K k 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 22． 某车间为了规定工时额定，需要确定加工零件所花费的时间，为此作了 6次试验，得 到数据如下： 零件数 x /个 10 20 30 40 50 60 加工时间 y /min 64 70 77 82 90 97 （1）试对上述变量 x 与 y 的关系进行相关性检验，如果 x 与 y 具有线性相关关系，求出 y 对 x 的回归直线方程； （2）根据（ 1）的结论，你认为每小时加工零件的数量额定为多少（四舍五入为整数）比 较合理？ 附：相关性检验的临界值表 2n 小概率 0.05 0.01 3 0.878 0.959 4 0.811 0.917 5 0.754 0.874 6 0.707 0.834 1 1 2 2 2 22 2 1 1 1 1 n n i i i i i i n n n n i i i i i i i i x x y y x y nx y r x x y y x nx y ny 1 1 2 22 1 1 n n i i i i i i n n i i i i x x y y x y nx y b x x x nx $ ， $ $y a bx$ 参考数据： 1750 42.0 ； 758 27.5 6 1 i i i x y 6 2 1 i i x 6 2 1 i i y 6 2 1 i i x x 6 2 1 i i y y 17950 9100 39158 1750 758 23． 自由购是一种通过自助结算购物的形式．某大型超市为调查顾客自由购的使用情况， 随机抽取了 100 人，调查结果整理如下： 20 以下 [20 ， 30） [30， 40） [40， 50） [50， 60） [60 ，70] 70 以上 使用人数 3 12 17 6 4 2 0 未使用人数 0 0 3 14 36 3 0 （1）现随机抽取 1 名顾客，试估计该顾客年龄在 [30，50）且未使用自由购的概率； （2）从被抽取的年龄在 [50，70]使用的自由购顾客中，随机抽取 2 人进一步了解情况，求 这 2 人年龄都在 [50，60）的概率； （3）为鼓励顾客使用自由购，该超市拟对使用自由购顾客赠送 1 个环保购物袋．若某日该 超市预计有 5000 人购物，试估计该超市当天至少应准备多少个环保购物袋？ 24． 艾滋病是一种危害性极大的传染病，由感染艾滋病病毒 (HIV 病毒 ) 引起，它把人体 免疫系统中最重要的 CD4T 淋巴细胞作为主要攻击目标，使人体丧失免疫功能 .下表是近八 年来我国艾滋病病毒感染人数统计表： 年份 2011 2012 2013 2014 2015 2016 2017 2018 年份代码 x 1 2 3 4 5 6 7 8 感染者人 数 (y 单 位：万人 ) 34.3 38.3 43.3 53.8 57.7 65.4 71.8 85 1 请根据该统计表，画出这八年我国艾滋病病毒感染人数的折线图； 2 请用相关系数说明：能用线性回归模型拟合 y 与 x 的关系； 3 建立 y 关于 x 的回归方程 ( 系数精确到 0.01) ，预测 2019 年我国艾滋病病毒感染人 数． 参考数据： 42 6.48； 8 1 449.6i i y ， 8 1 2319.5i i i x y ， 8 2 1 ( ) 46.2i i y y ， 参考公式：相关系数 1 2 2 1 1 ( ) ( ) ( ) n i ii n n i ii i x x y y r x x y y ， 回归方程 y bx a$ $ $ 中， b$ 1 2 1 ( ) ( ) n i ii n ii x x y y x x ， a y bx$ $ ． 25． 为提高产品质量，某企业质量管理部门经常不定期地抽查产品进行检测，现在某条生 产线上随机抽取 100 个产品进行相关数据的对比，并对每个产品进行综合评分（满分 100 分），将每个产品所得的综合评分制成如图所示的频率分布直方图 .记综合评分为 80 分及 以上的产品为一等品 . （1）求图中 a 的值，并求综合评分的中位数； （2）用样本估计总体，以频率作为概率，按分层抽样的思想，先在该条生产线中随机抽取 5 个产品，再从这 5 个产品中随机抽取 2 个产品记录有关数据，求这 2 个产品中恰有一个一 等品的概率 . 26． 某地随着经济的发展，居民收入逐年增长该地一建设银行统计连续五年的储蓄存款 （年底余额）得到下表： 年份 x 2014 2015 2016 2017 2018 储蓄存款 y（千亿元） 5 6 7 8 10 为便于计算，工作人员将上表的数据进行了处理（令 2013,t x 5z y ），得到下 表： 时间 t 1 2 3 4 5 储蓄存款 z 0 1 2 3 5 （1）求 z关于 t 的线性回归方程； （2）通过（ 1）中的方程，求出 y 关于 x 的回归方程； （3）用所求回归方程预测到 2020 年年底，该地储蓄存款额可达多少？ 附：线性回归方程 ?? ?y bx a ，其中 1 2 2 1 ? n i i i n i i x y nx y b x nx ， ??a y bx . 【参考答案】 *** 试卷处理标记，请不要删除 一、选择题 1．C 解析： C 【解析】 【分析】 等差数列的性质．渗透了数据分析素养．使用统计思想，逐个选项判断得出答案． 【详解】 详解：由已知将 1000 名学生分成 100 个组，每组 10 名学生，用系统抽样， 46 号学生被抽 到， 所以第一组抽到 6 号，且每组抽到的学生号构成等差数列 { }na ，公差 10d ， 所以 6 10na n ( )n N ， 若 8 6 10n，则 1 5 n ，不合题意；若 200 6 10n，则 19.4n ，不合题意； 若 616 6 10n，则 61n ，符合题意；若 815 6 10n ，则 80.9n ，不合题意．故 选 C． 【点睛】 本题主要考查系统抽样 . 2．C 解析： C 【解析】 【分析】 分别求出③和④的巧板的面积，根据几何概型的概率关系转化为面积比 . 【详解】 设巧板①的边长为 1，则结合图 2 可知大正方形的边长为 3， 其面积 23 9S .其中巧板③是底边长为 2 的等腰直角三角形， 其面积为 1 1 2 1 1 2 S ，巧板④可看作是边长为 2 的正方形 与腰长为 1 的等腰直角三角形的组合图形， 其面积为 2 2 1 51 1 ( 2) 2 2 S ， 故所求的概率 1 2 7 18 S SP S . 故选 :C. 【点睛】 本题考查几何概型的概率求法，转化为面积比，属于中档题 . 3．C 解析： C 【解析】 【分析】 甲、乙两人各写一张贺年卡随意送给丙、丁两人中的一人共有 4 种情况，甲、乙将贺年卡 都送给丁有 1 种情况，利用古典概型求解即可． 【详解】 （甲送给丙、乙送给丁）、（甲送给丁，乙送给丙）、（甲、乙都送给丙）、（甲、乙都 送给丁）共四种情况，其中甲、乙将贺年卡送给同一人的情况有两种， 所以甲、乙将贺年卡送给同一人丁的情况一种，概率是： 1 4 ， 故选 C． 【点睛】 本题主要考查了古典概型的定义及计算，排列，计数原理，属于中档题． 4．A 解析： A 【解析】 分析：可以按照等可能时间的概率来考虑，可以先列举出试验发生包含的事件数，再求出 满足条件的事件数，从而根据概率计算公式求解 . 详解：因为 a 是抛掷一枚骰子得到的点数，所以试验发生包含的事件总数为 6， 方程 2 2 0x ax 有两个不等实根，所以 2 8 0a ， 以为 a 为正整数，所以 3,4,5,6a ， 即满足条件的事件有 4种结果，所以所求的概率为 4 2 6 3 P ，故选 A. 点睛：本题主要考查的是古典概型及其概率计算公式 .，属于基础题．解题时要准确理解题 意，先要判断该概率模型是不是古典概型，利用排列组合有关知识，正确找出随机事件 A 包含的基本事件的个数和试验中基本事件的总数代入公式 n A P n . 5．B 解析： B 【解析】 【分析】 根据频率分布直方图的性质和频率分布直方图中样本估计总体，准确运算，即可求解 . 【详解】 由题意，根据频率分布直方图的性质得 10( 0.020 0.016 0.016 0.011 0.006) 1m ， 解得 0.031m . 故①正确； 因为不低于 140 分的频率为 0.011 10 0.11，所以 110 1000 0.11 n ，故②错误； 由 100 分以下的频率为 0.006 10=0.06 ，所以 100 分以下的人数为 1000 0.06=60 ， 故③正确； 分数在区间 [120,140)的人数占 0.031 10 0.016 10 0.47，占小半 . 故④错误 . 所以说法正确的是①③. 故选 B. 【点睛】 本题主要考查了频率分布直方图的应用，其中解答熟记频率分布直方图的性质，以及在频 率分布直方图中，各小长方形的面积表示相应各组的频率，所有小长方形的面积的和等于 1，着重考查了分析问题和解答问题的能力，属于基础题 . 6．B 解析： B 【解析】 【分析】 根据互斥事件的定义，逐个判断，即可得出正确选项． 【详解】 A为三件产品全不是次品，指的是三件产品都是正品， B 为三件产品全是次品， C 为三件产品不全是次品，它包括一件次品，两件次品，三件全是正品三个事件 由此知： A与 B 是互斥事件； A与 C 是包含关系，不是互斥事件； B 与 C 是互斥事件， 故选 B． 【点睛】 本题主要考查互斥事件定义的应用． 7．B 解析： B 【解析】 分析：根据程序框图可知先对奇数项累加，偶数项累加，最后再相减 . 因此累加量为隔项 . 详解：由 1 1 1 1 11 2 3 4 99 100 S 得程序框图先对奇数项累加，偶数项累加，最 后再相减 . 因此在空白框中应填入 2i i ，选 B. 点睛：算法与流程图的考查，侧重于对流程图循环结构的考查 . 先明晰算法及流程图的相关 概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终 止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项 . 8．C 解析： C 【解析】 【分析】 由题意结合均值不等式的结论即可求得 1 4y a b 的最小值，注意等号成立的条件 . 【详解】 由题意可得： 1 4y a b 1 1 4 1 45 2 2 b aa b a b a b 1 45 2 2 b a a b 9 2 ， 当且仅当 2 4, 3 3 a b 时等号成立 . 即 1 4y a b 的最小值是 9 2 . 故选： C. 【点睛】 在应用基本不等式求最值时，要把握不等式成立的三个条件，就是 “一正 —— 各项均为正； 二定 —— 积或和为定值；三相等 —— 等号能否取得 ”，若忽略了某个条件，就会出现错误． 9．D 解析： D 【解析】 运行该程序，第一次， 1,k 2x , 第二次， 2,k 3x ， 第三次， 4,k 4x ， 第四次， 16,k 5x ， 第五次， 4,k 6x ， 第六次， 16,k 7x ， 第七次， 4,k 8x ， 第八次， 16,k 9x ， 观察可知， 若判断框中为 5k ．，则第四次结束，输出 x 的值为 16，满足； 若判断框中为 4k ．，则第四次结束，输出 x 的值为 16，满足； 若判断框中为 9k ．，则第八次结束，输出 x 的值为 16，满足； 若判断框中为 7k ．，则第七次结束，输出 x 的值为 4，不满足； 故选 D. 10．A 解析： A 【解析】 【分析】 根据所给的程序运行结果为 ，执行循环语句，当计算结果 S 为 20 时，不满足判断框 的条件，退出循环，从而到结论． 【详解】 由题意可知输出结果为 ， 第 1 次循环， ， ， 第 2 次循环， ， ， 此时 S 满足输出结果，退出循环，所以判断框中的条件为 ． 故选： A． 【点睛】 本题主要考查了循环结构，是当型循环，当满足条件，执行循环，同时考查了推理能力， 属于基础题． 11．B 解析： B 【解析】 分析：由题意逐一考查所给的说法是否正确即可 . 详解：逐一考查所给的说法： ①由分层抽样的概念可知，取东部地区学生 2400100 2400 1600 1000 48 人、 中部地区学生 1600100 2400 1600 1000 32 人、 西部地区学生 1000100 2400 1600 1000 20 人，题中的说法正确； ②新生的人数较多，不适合用简单随机抽样的方法抽取人数，题中的说法错误； ③西部地区学生小刘被选中的概率为 100 1 2400 1600 1000 50 ，题中的说法正确； ④中部地区学生小张被选中的概率为 100 1 2400 1600 1000 50 ，题中的说法错误； 综上可得，正确的说法是①③ . 本题选择 B 选项 . 点睛：本题主要考查分层抽样的概念，简单随机抽样的特征，古典概型概率公式等知识， 意在考查学生的转化能力和计算求解能力 . 12．B 解析： B 【解析】 试题分析：由题 ， ，所以 ． 试题解析：由已知 ， 又因为 ?? ?y bx a ， ? ??0.76,b a y bx 所以 ，即该家庭支出为 万元． 考点：线性回归与变量间的关系． 二、填空题 13．【解析】【分析】执行如图所示的程序框图逐次计算根据判断条件即可求 解得到答案【详解】执行如图所示的程序框图可得：第 1 次循环满足判断条 件；第 2 次循环满足判断条件；第 3 次循环满足判断条件；第 4 次循环满足判 解析： 6 【解析】 【分析】 执行如图所示的程序框图，逐次计算，根据判断条件，即可求解，得到答案 . 【详解】 执行如图所示的程序框图，可得： 0, 1S m ， 第 1 次循环，满足判断条件， 10 1 2 2, 2S m ； 第 2 次循环，满足判断条件， 22 2 2 10, 3S m ； 第 3 次循环，满足判断条件， 310 3 2 34, 4S m ； 第 4 次循环，满足判断条件， 434 4 2 98, 5S m ； 第 5 次循环，满足判断条件， 598 5 2 258, 6S m ； 不满足判断条件，此时输出 6m . 故答案为 6. 【点睛】 本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中根据给定的程序框 图，逐次计算，结合判断条件求解是解答的关键，着重考查了推理与运算能力，属于基础 题. 14．7【解析】【分析】根据系统抽样的定义和抽取方法求得样本间隔进行抽取 即可求解得到答案【详解】由题意从该校高一年级全体 800名学生中抽 50名学生 其样本间隔为因为在 33～48这 16个数中取的数是 39所以从 解析： 7 【解析】 【分析】 根据系统抽样的定义和抽取方法，求得样本间隔，进行抽取，即可求解，得到答案． 【详解】 由题意，从该校高一年级全体 800 名学生中抽 50 名学生，其样本间隔为 800 16 50 ， 因为在 33～48 这 16 个数中取的数是 39， 所以从 33～48 这 16 个数中取的数是第 3 个数， 所以第 1 组 1～16 中随机抽到的数是 39 2 16 7 ． 【点睛】 本题主要考查了系统抽样的应用，其中解答中熟记系统抽样的概念和抽取的方法，准确计 算是解答的关键，着重考查了运算与求解能力，属于基础题． 15．【解析】【分析】先求出总的基本事件的总数再求出点数之积为奇数的基 本事件的总数再利用古典概型的概率公式求解【详解】由题得总的基本事件个 数为两次点数之积为奇数的基本事件的个数为由古典概型的概率公式得故答 解析： 1 4 【解析】 【分析】 先求出总的基本事件的总数，再求出点数之积为奇数的基本事件的总数，再利用古典概型 的概率公式求解 . 【详解】 由题得总的基本事件个数为 6 6=36 ，两次点数之积为奇数的基本事件的个数为 3 3=9 ， 由古典概型的概率公式得 9 1 36 4 P . 故答案为： 1 4 【点睛】 本题主要考查古典概型的概率公式的计算，意在考查学生对这些知识的理解掌握水平和分 析推理能力 . 16．【解析】从分别写有 12345 的 5 张卡片中随机抽取 1 张放回后再随机抽取 1 张 基本事件总数 n=5×5=25 抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有： （21）（ 31）（ 32）（41） 解析： 2 5 【解析】 从分别写有 1，2，3，4，5 的 5 张卡片中随机抽取 1 张，放回后再随机抽取 1 张， 基本事件总数 n=5×5=25， 抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有： （2，1），（ 3，1），（ 3，2），（ 4，1），（ 4，2），（ 4，3），（ 5， 1），（ 5， 2），（ 5，3），（ 5，4）， 共有 m=10 个基本事件， ∴抽得的第一张卡片上的数大于第二张卡片上的数的概率 p= 2 . 5 故答案为 2 5 . 17．8【解析】【分析】根据茎叶图计算平均数【详解】由茎叶图得【点睛】本 题考查茎叶图以及平均数考查基本运算能力属基础题 解析： 8 【解析】 【分析】 根据茎叶图计算平均数 . 【详解】 由茎叶图得 16 17 10 19 2018 8. 5 x x 【点睛】 本题考查茎叶图以及平均数，考查基本运算能力，属基础题 . 18．7【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐 次计算直到达到输出条件即可得到输出的值【详解】由程序框图可知：则因此 输出的为故答案为 7【点睛】本题主要考查程序框图的循环结构流程图属 解析： 7 【解析】 【分析】 模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 得到输出 a 的值 . 【详解】 由程序框图可知： 98 63a b ， 35 98 63, 28 63 35a b ， 7 35 28, 21 28 7a b ， 14 21 7, 7 21 14a b ， 7 14 7a ，则 7a b ，因此输出的 a 为 7 ，故答案为 7. 【点睛】 本题主要考查程序框图的循环结构流程图，属于中档题 . 解决程序框图问题时一定注意以下 几点： (1) 不要混淆处理框和输入框； (2) 注意区分程序框图是条件分支结构还是循环结 构； (3) 注意区分当型循环结构和直到型循环结构； (4) 处理循环结构的问题时一定要正确 控制循环次数； (5) 要注意各个框的顺序 ,（6）在给出程序框图求解输出结果的试题中只要 按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 . 19．【解析】根据分层抽样的方法可得解得所以若从高校抽取的人中选人作专 题发言共有种情况则这二人都来自高校共有种情况所以概率为点睛：本题主要 考查了分层抽样和古典概型及其概率的计算问题其中解答中涉及分层抽样的 解析： 3 10 【解析】 根据分层抽样的方法，可得 2 36 18 54 x y ，解得 1, 3x y ， 所以若从高校 ,B C 抽取的人中选 2 人作专题发言，共有 10种情况， 则这二人都来自高校 C 共有 3 种情况，所以概率为 3( ) 10 P C ． 点睛：本题主要考查了分层抽样和古典概型及其概率的计算问题，其中解答中涉及分层抽 样的方法的计算，古典概型及其概率计算的公式的应用，试题比较基础，属于基础题，解 答中牢记古典概型及其概率的求解是解答的关键． 20．64【解析】结合频率分布直方图可得平均分为：即这些学生的平均分为 64 分点睛：利用频率分布直方图求众数中位数和平均数时应注意三点： ① 最高的 小长方形底边中点的横坐标即是众数； ② 中位数左边和右边的小长方形 解析： 64 【解析】 结合频率分布直方图可得，平均分为： 50 0.020 10 60 0.040 10 70 0.025 10 80 0.010 10 90 0.005 10 64 ， 即这些学生的平均分为 64 分 . 点睛：利用频率分布直方图求众数、中位数和平均数时，应注意三点：①最高的小长方形 底边中点的横坐标即是众数；②中位数左边和右边的小长方形的面积和是相等的；③平均 数是频率分布直方图的 “重心 ”，等于频率分布直方图中每个小长方形的面积乘以小长方形 底边中点的横坐标之和 . 三、解答题 21． （1） 75.5；（ 2）列联表见解析，没有 . 【解析】 试题分析：（ 1）各小矩形中点横坐标与纵坐标的乘积的和即是对此事关注的同学的物理期 末平均分；（ 2）根据直方图求出列联表所需数据，即可完成 2 2 列联表，利用公式 2 2 n ad bc k a b c d a c b d 求得 2K ，与邻界值比较，即可得到结论 . 试题解析：（ 1）对此事关注的同学的物理期末平均分为 (45 0.005 55 0.005 65 0.020 75 0.030 85 0.030 95 0.010) 10 75.5 （分）． （2）①补充的 2 2列联表如下： 物理成绩优秀 物理成绩不优秀 合计 对此事关注 8 12 20 对此事不关注 8 32 40 合计 16 44 60 ②由①中的列联表可得 2 2 n ad bc k a b c d a c b d 2 60 8 32 8 12 16 44 20 40 30 2.73 3.841 11 ， 所以没有 95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系． 【方法点睛】本题主要考查频率分布直方图的应用以及独立性检验，属于中档题 . 独立性检 验的一般步骤：（ 1）根据样本数据制成 2 2 列联表；（ 2）根据公式 2 2 n ad bc K a b a d a c b d 计算 2K 的值； (3) 查表比较 2K 与临界值的大小关 系，作统计判断 . （注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到 的结论也可能犯错误 . ） 22． （1）答案见解析 .（ 2） 96 【解析】 【分析】 （1）根据表中所给数据，计算出 | |r ，即可求得答案 . （2）每小时加工零件的数量，即 60x ，将 60x 代入 ? 0.657 57y x ，即可求得答案 . 【详解】 （1）由表中数据得： 6 1 17950i i i x y ， 6 2 1 9100i i x ， 6 2 1 39158i i y ， 35, 80x y 0.052 2 17950 6 35 80| | 0.997 9100 6 35 39158 6 80 r r 从而有 95%的把握认为 x 与 y 之间具有线性相关关系， 此求回归直线方程是有意义的． 计算得： ? ?0.657, 57b a ? 0.657 57y x （2）Q 每小时加工零件的数量，即 60x 将 60x 代入 ? 0.657 57y x ? 96.42y 故每小时加工零件的数量额定为 96 比较合理 【点睛】 本题考查回归直线方程以及应用，考查基本分析与求解能力，属基本题 . 23． （1） 17 100 ．（ 2） 2 5 ；（ 3） 2200个 【解析】 【分析】 （1）直接计算概率得到答案 . （2）列出所有情况，包含 15 个基本事件，满足条件的共有 6 个基本事件，计算得到概率 . （3）按照比例关系计算得到答案 . 【详解】 （1）随机抽取的 100 名顾客中，年龄在 [30，50）且未使用自由购的有 3+14＝17 人， 所以随机抽取一名顾客，该顾客年龄在 [30，50）且未参加自由购的概率估计为 17 100 P ． （2）设事件 A 为“这 2 人年龄都在 [50，60）”. 被抽取的年龄在 [50，60）的 4 人分别记为 a1，a2，a3，a4， 被抽取的年龄在 [60，70]的 2 人分别记为 b1，b2， 从被抽取的年龄在 [50，70]的自由购顾客中随机抽取 2 人 共包含 15 个基本事件， 分别为 a1a2，a1a3，a1a4，a1b1，a1b2，a2a3，a2a4，a2b1， a2b2， a3a4， a3b1，a3b2，a4b1， a4b2， b1b2， 事件 A 包含 6 个基本事件， 分别为 a1a2，a1a3，a1a4，a2a3，a2a4，a3a4， 则 6 2 15 5 P A ； （3）随机抽取的 100 名顾客中，使用自由购的有 3+12+17+6+4+2 ＝44 人， 所以该超市当天至少应准备环保购物袋的个数估计为 44 5000 2200 100 ． 【点睛】 本题考查了概率的计算，总体估计，意在考查学生的计算能力和应用能力 . 24． （1）见解析；（ 2）见解析；（ 3）预测 2019 年我国艾滋病感染累积人数为 87.93万 人 【解析】 【分析】 （1）由所给的数据绘制折线图即可；（ 2）由题意计算相关系数来说明变量之间的相关关 系即可；（ 3）首先求得回归方程，然后利用回归方程的预测作用进行预测即可． 【详解】 解：（ 1）我国艾滋病病毒感染人数的折线图如图所示 92 , 56.2 2 x yQ ， 1 1 8 8 ( ) 8 296.3 i i i i i ix x y y x y xy ， 1 1 2 2 8 8 ( ) ( ) 42 46.2 299.376 i i i ix x y y ， 1 2 2 1 1 ( ) 0.99 ( ) ( ) n i i i n n i i i i x x y y r x x y y ． 故具有强线性相关关系． 1 2 1 ( ) 296.33 7.05 ( ) 42 n i i i n i i x x y y b x x $ Q ， 56.2 7.05 4.5 24.48a y b x $ $ ， 7.05 24.48y x $ ． 当 9x 时， 7.05 9 24.48 87.93y ． 故预测 2019 年我国艾滋病感染累积人数为 87.93万人． 【点睛】 本题主要考查线性回归方程的求解与预测作用，相关系数的计算与含义等知识，意在考查 学生的转化能力和计算求解能力． 25． (1) 0.040a ；中位数为 82.5. (2) 3 5 【解析】 【分析】 （1）根据频率之和为 1，结合频率分布直方图对应矩形区域面积求解即可；先结合数值预 判中位数所在组距应在 80 到 90 之间，设综合评分的中位数为 x ，结合频率计算公式求解 即可； （2）先结合分层抽样计算出一等品所占比例，再采用列举法表示出所有基本事件，结合古 典概率公式求解即可 【详解】 （1）由频率和为 1，得 (0.005 0.010 0.025 0.020) 10 1a ， 0.040a ； 设综合评分的中位数为 x ，则 (0.005 0.010 0.025) 10 0.040 ( 80) 0.5x ，解得 82.5x ， 所以综合评分的中位数为 82.5. （2）由频率分布直方图知，一等品的频率为 (0.040 0.020) 10 0.6 ，即概率为 0.6； 所以 100 个产品中一等品有 60 个，非一等品有 40 个，则一等品与非一等品的抽样比为 3：2； 所以现抽取 5 个产品，一等品有 3 个，记为 a 、 b 、 c ，非一等品 2 个，记为 D 、 E ； 从这 5 个产品中随机抽取 2 个，基本事件为： ab 、 ac 、 aD 、 aE 、 bc 、 bD 、 bE 、 cD 、 cE 、 DE 共 10 种； 抽取的这 2 个产品中恰有一个一等品的事件为： aD 、 aE 、 bD 、 bE 、 cD 、 cE 共 6 种， 所以所求的概率为 6 3 10 5 P . 【点睛】 本题考查频率分布直方图中具体数值的求解，中位数的计算，求解具体事件对应的概率， 属于中档题 26． （1） 1.2 1.4z t$ （ 2） $ 1.2 2412y x （3） 12 千亿元 【解析】 【分析】 （1）求出 t 、 z、 1 5 i i i t z 、 5 2 1 i i t 后代入公式即可得解； （2）由题意可得 $ 5 1.2 2013 1.4y x ，化简即可得解； （3）把 2020x 代入线性回归方程即可得解 . 【详解】 （1）由题意 1 1 2 3 4 5 3 5 t ， 1 0 1 2 3 5 2.2 5 z ， 则 5 1 1 0 2 1 3 2 4 3 5 5 45i i i t z ， 5 2 1 1 4 9 16 25 55i i t ， 5 5 1 22 1 5 45 5 3 2.2? 1.2 55 5 9 i i i i i t z t z b t nt ， ?? 2.2 1.2 3 1.4a z bt ， 1.2 1.4z t$ . （2）由令 2013,t x 5z y ，结合（ 1）中结论可得 $ 5 1.2 2013 1.4y x 即 $ 1.2 2412y x （3）由题意，当 2020x 时， $ 1.2 2020 2412 12y ， 所以可预测到 2020 年年底，该地储蓄存款额可达 12 千亿元 . 【点睛】 本题考查了线性回归方程的求解和应用，考查了计算能力，属于中档题 .