2018届二轮复习　带电粒子在磁场中的运动课件(共32张)

2018届二轮复习　带电粒子在磁场中的运动课件(共32张)

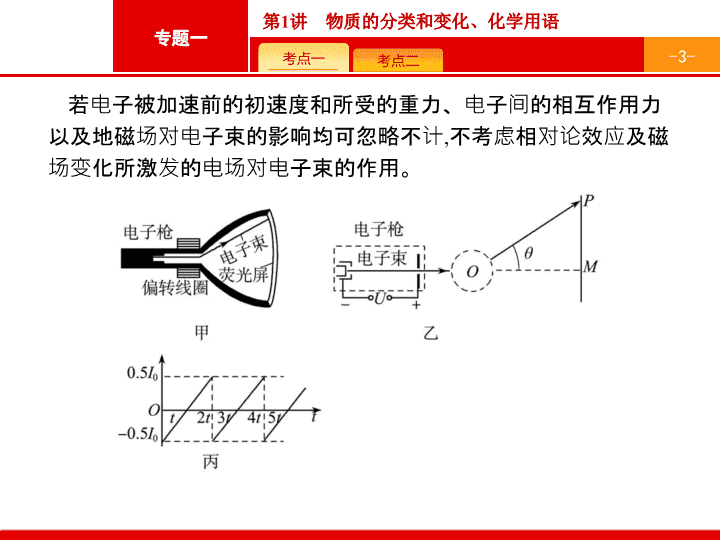
第 11 讲　带电粒子在磁场中的运动 - 2 - 带电粒子在有界磁场中运动问题 【典题 1 】 电视机中显像管 ( 抽成真空玻璃管 ) 的成像原理主要是靠电子枪产生高速电子束 , 并在变化的磁场作用下发生偏转 , 打在荧光屏不同位置上发出荧光而形成像。显像管的原理示意图 ( 俯视图 ) 如图甲所示 , 在电子枪右侧的偏转线圈可以产生使电子束沿纸面发生偏转的磁场 , 偏转的磁场可简化为由通电螺线管产生的与纸面垂直的磁场 , 该磁场分布的区域为圆形 ( 如图乙所示 ), 其磁感应强度 B= μ NI , 式中 μ 为磁常量 , N 为螺线管线圈的匝数 , I 为线圈中电流的大小。由于电子的速度极大 , 同一电子穿过磁场过程中可认为磁场没有变化 , 是稳定的匀强磁场。已知电子质量为 m , 电荷量为 e , 电子枪加速电压为 U , 磁常量为 μ , 螺线管线圈的匝数为 N , 偏转磁场区域的半径为 r , 其圆心为 O 点。当没有磁场时 , 电子束通过 O 点 , 打在荧光屏正中的 M 点 , O 点到荧光屏中心的距离 OM=L 。 - 3 - 若电子被加速前的初速度和所受的重力、电子间的相互作用力以及地磁场对电子束的影响均可忽略不计 , 不考虑相对论效应及磁场变化所激发的电场对电子束的作用。 - 4 - (1) 求电子束经偏转磁场后打到荧光屏上 P 点时的速率 ; (2) 若电子束经偏转磁场后速度的偏转角 θ = 60 ° , 求此种情况下电子穿过磁场时 , 螺线管线圈中电流 I 0 的大小 ; (3) 当线圈中通入如图丙所示的电流 , 其最大值为第 (2) 问中电流 的 。 求电子束打在荧光屏上发光所形成 “ 亮线 ” 的长度。 - 5 - (2) 设电子在磁场中运动的半径为 R , 运动轨迹如图所示 。 (3) 设线圈中电流为 0 . 5 I 0 时偏转角为 θ 1 , 此时电子在屏幕上落点距 M 点最远。 - 6 - 解题技法 1 . 圆心的 确定 (1) 已知入射点、入射方向和出射点、出射方向时 , 可通过入射点和出射点作垂直于入射方向和出射方向的直线 , 两条直线的交点就是圆弧轨道的圆心 ( 图甲所示 ) 。 (2) 已知入射方向和入射点、出射点的位置时 , 可以通过入射点作入射方向的垂线 , 连接入射点和出射点 , 作其中垂线 , 这两条垂线的交点就是圆弧轨道的圆心 ( 图乙所示 ) 。 - 7 - (3) 带电粒子在不同边界磁场中的运动 : ① 直线边界 ( 进出磁场具有对称性 , 如图所示 ) 。 ② 平行边界 ( 存在临界条件 , 如图所示 ) 。 - 8 - ③ 圆形边界 ( 沿径向射入必沿径向射出 , 如图所示 ) 。 - 9 - 2 . 半径的确定和计算 利用平面几何关系 , 求出该圆的可能半径 ( 或圆心角 ), 求解时注意以下几个重要的几何特点 : (1) 粒子速度的偏向角 ( φ ) 等于圆心角 ( α ), 并等于 AB 弦与切线的夹角 ( 弦切角 θ ) 的 2 倍 ( 如图所示 ), 即 φ = α = 2 θ 。 (2) 直角三角形的应用 ( 勾股定理 ): 找到 AB 的中点 C , 连接 OC , 则 △ AOC 、 △ BOC 都是直角三角形。 - 10 - 3 . 运动时间的确定 粒子在磁场中运动一周的时间为 T , 当粒子运动的圆弧所对应的圆心角为 α 时 , 其运动时间可由下式表示 : - 11 - 当堂练 1 　 如图 , 直角坐标系在一真空区域里 , y 轴的左方有一匀强电场 , 电场强度方向跟 y 轴负方向成 θ = 30 ° , y 轴右方有一垂直于坐标系平面的匀强磁场 , 在 x 轴上的 A 点有一质子发射器 , 它向 x 轴的正方向发射速度大小为 v= 2 . 0 × 10 6 m/s 的质子 , 质子经磁场在 y 轴的 P 点射出磁场 , 射出方向恰垂直于电场的方向 , 质子在电场中经过一段时间 , 运动到 x 轴的 Q 点。已知 A 点与原点 O 的距离为 10 cm, Q 点 与 - 12 - 求 :(1) 磁感应强度的大小和方向 ; (2) 质子在磁场中运动的时间 ; (3) 电场强度的大小。 答案 : (1)0 . 1 T, 方向垂直于纸面向里 　 (2 ) × 10 - 7 s 　 (3)1 . 0 × 10 5 N/C 解析 : (1) 设质子在磁场中做圆周运动的半径为 r 。 如图 , 由几何关系得 α = θ = 30 ° , 所以 r= 2 OA= 20 cm - 13 - (3) 由 P 到 Q , 质子做类平抛运动 , 图中 , 由几何关系得 β = 30 ° , 则 2 r=vt - 14 - 带电粒子在磁场中运动的临界、极值问题 【典题 2 】 (2017 浙江选考 10 月 ,23) 如图所示 , x 轴上方存在垂直纸面向外的匀强磁场 , 坐标原点处有一正离子源 , 单位时间在 xOy 平面内发射 n 0 个速率均为 v 的离子 , 分布在 y 轴两侧各为 θ 的范围内。在 x 轴上放置长度为 L 的离子收集板 , 其右端点距坐标原点的距离为 2 L , 当磁感应强度为 B 0 时 , 沿 y 轴正方向入射的离子 , 恰好打在收集板的右端点。整个装置处于真空中 , 不计重力 , 不考虑离子间的碰撞 , 忽略离子间相互作用。 - 15 - (1) 求离子的 比荷 ; (2) 若发射的离子被收集板全部收集 , 求 θ 的最大值 ; (3) 假设离子到达 x 轴时沿 x 轴均匀分布。当 θ = 37 ° , 磁感应强度在 B 0 ≤ B ≤ 3 B 0 的区间取不同值时 , 求单位时间内收集板收集到的离子数 n 与磁感应强度 B 之间的关系。 ( 不计离子在磁场中运动的时间 ) - 16 - (2) 如图 1 所示 , 以最大值 θ m 入射时 , 有 Δ x= 2 R (1 - cos θ m ) =L 或 2 R cos θ m =L - 17 - (3) B>B 0 , 全部收集到离子时的最小半径为 R 1 , 如图 2, 有 2 R 1 cos 37 ° =L 当 2 B 0 1 . 6 B 0 , 恰好收集不到离子时的半径为 R 2 , 有 R 2 = 0 . 5 L 得 B 2 = 2 B 0 当 1 . 6 B 0

查看更多