2014届高三物理(教科版)第一轮复习自主学习训练 2-2
2 匀速圆周运动的向心力和向心加速度
(时间:60分钟)
知识点
基础
中档
稍难
对向心力的
理解和应用
2、3、4、5
1
对向心加速度的
理解及应用
6、7
8
综合提升
9、10、11
12
知识点一 对向心力的理解和应用
1.如图2-2-8所示,A、B、C三个物体放在旋转圆台上,动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴为R,C离轴为2R.当圆台旋转时,则
( ).
图2-2-8
A.若A、B、C均未滑动,则C的向心加速度最大
B.若A、B、C均未滑动,则B的摩擦力最小
C.当圆台转速增大时,B比A先滑动
D.圆台转速增大时,C比B先滑动
解析 三个物体在圆台上,以相同的角速度做圆周运动,其向心力是由f静提供的,F=ma=mω2R,静摩擦力的大小由m、ω、R三者决定,其中ω相同.
而RA=RC,mA=2mC,所以FA=FC,mB=mC,RB
FB,故FB最小,B选项正确.
当圆台转速增大时,f静都随之增大,当增大至刚好要滑动时,达到最大静摩擦力.
μmg=mω2R,而ωA=ωB,RA=RB,mA=2mB
FA=2FB,而fmaxA=2fmaxB,所以B与A将同时滑动,C错.
RC=2RB,mB=mC,而FC>FB,而fmaxC=fmaxB,所以C比B先滑动,故选项A、B、D正确.
答案 ABD
2.如图2-2-9所示,一小球用细绳悬挂于O点,将其拉离竖直位置一个角度后释放,则小球以O点为圆心做圆周运动,运动中小球所需的向心力是 ( ).
A.绳的拉力
图2-2-9
B.重力和绳拉力的合力
C.重力和绳拉力的合力沿绳方向的分力
D.绳的拉力和重力沿绳方向分力的合力
解析 对小球受力分析如右图所示,小球受重力和绳子拉力作用,向心力是指向圆心方向的合外力,它可以是小球所受合力沿绳子方向的分力,也可以是各力沿绳方向的分力的合力,正确选项为C、D.
答案 CD
图2-2-10
3.如图2-2-10所示,长为L的悬线固定在O点,在O点正下方处有一钉子C,把悬线另一端的小球m拉到跟悬点在同一水平面上无初速度释放,小球运动到悬点正下方时悬线碰到钉子,则小球的 ( ).
A.线速度突然增大 B.角速度突然增大
C.向心加速度突然增大 D.悬线拉力突然增大
解析 悬线与钉子碰撞前后,线的拉力始终与球运动方向垂直,故小球的线速度不变.当半径减小时,由ω=知ω变大,再由F向=m知向心加速度突然增大.而在最低点F向=F-mg,故悬线拉力变大.由此可知,B、C、D选项正确.
答案 BCD
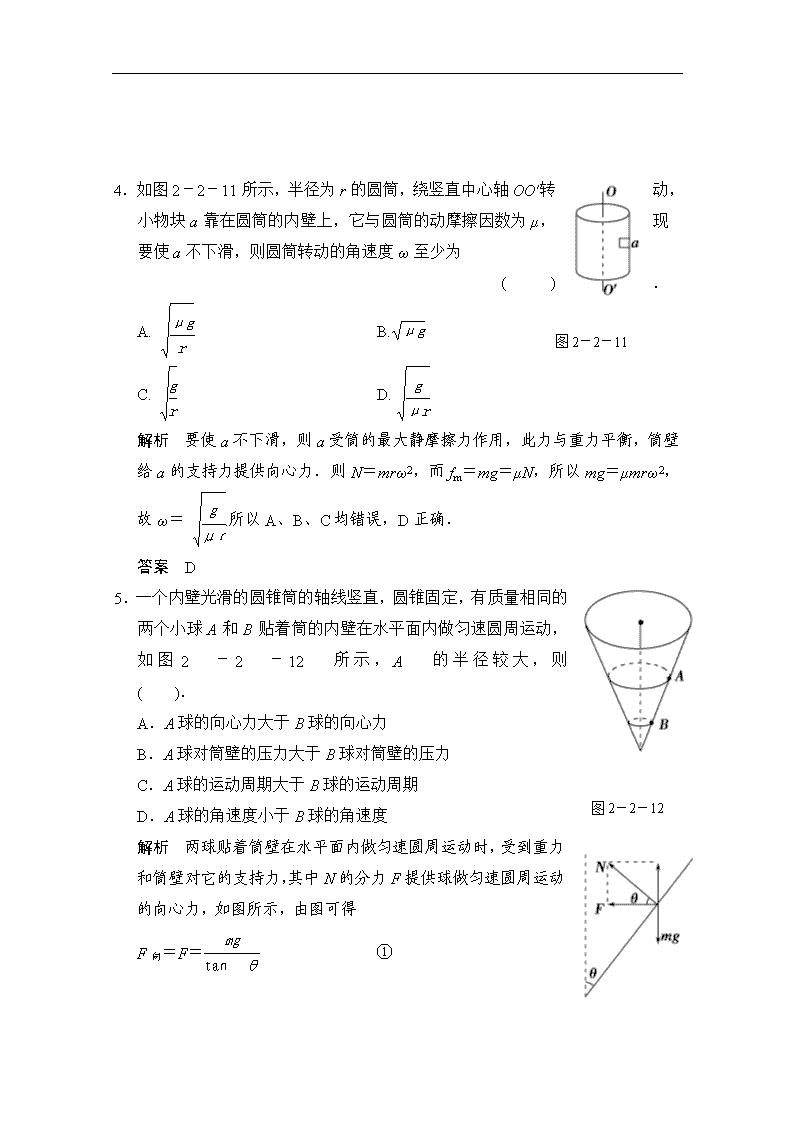
4.如图2-2-11所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为
( ).
图2-2-11
A. B.
C. D.
解析 要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力.则N=mrω2,而fm=mg=μN,所以mg=μmrω2,故ω= .所以A、B、C均错误,D正确.
答案 D
5.一个内壁光滑的圆锥筒的轴线竖直,圆锥固定,有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动,如图2-2-12所示,A的半径较大,则 ( ).
A.A球的向心力大于B球的向心力
B.A球对筒壁的压力大于B球对筒壁的压力
图2-2-12
C.A球的运动周期大于B球的运动周期
D.A球的角速度小于B球的角速度
解析 两球贴着筒壁在水平面内做匀速圆周运动时,受到重力和筒壁对它的支持力,其中N的分力F提供球做匀速圆周运动的向心力,如图所示,由图可得
F向=F= ①
N= ②
由上述两式可以看出,由于两个小球的质量相同,θ为定值,故A、B两球所受的向心力和它们对筒壁的压力大小是相等的,选项A
、B错误.由向心力的计算公式F=mrω2和F=
mr得
=mrω2,ω= ③
=mr,T=2π ④
由④可知TA>TB,所以C正确.
由③可知ωA<ωB,所以D正确.
答案 CD
知识点二 对向心加速度的理解及应用
6.一小球被细线拴着做匀速圆周运动,其半径为R,向心加速度为a,则 ( ).
A.小球相对于圆心的位移不变
B.小球的线速度为
C.小球在时间t内通过的路程s=
D.小球做圆周运动的周期T=2π
解析 小球做匀速圆周运动,各时刻相对圆心的位移大小不变,但方向时刻在变.
由a=得v2=Ra,所以v=,在时间t内通过的路程s=vt=t,做圆周运动的周期T====2π .
答案 BD
7.下列说法正确的是 ( ).
A.匀速圆周运动不是匀速运动而是匀变速运动
B.圆周运动的加速度一定指向圆心
C.向心加速度越大,物体速度的方向变化越快
D.因为a=,所以a与v2成正比
解析 匀速圆周运动,不是匀速也不是匀变速,因为其加速度的方向时刻改变,是变加速运动,故A不对;对变速圆周运动,不但速度方向改变,具有向心加速度,并且速度大小也发生改变,具有与速度在一条直线上的加速度,故其合加速度(实际加速度)不指向圆心,向心加速度就是描述速度方向发生改变的快慢,故B不对、C对.对公式a=只有当半径一定时才有关系a∝v2,D不对.
答案 C
8.关于地球上的物体随地球自转的向心加速度的大小,下列说法正确的是
( ).
A.在赤道上向心加速度最大
B.在两极向心加速度最大
C.在地球上各处,向心加速度一样大
D.随着纬度的升高,向心加速度的值逐渐减小
解析 地球上的物体随地球一起转动,在任何位置处转动的角速度都与地球自转的角速度相等.
由公式a=rω2可以知道,在角速度一定的情况下,向心加速度大小与转动半径成正比关系.所以,在赤道处,物体转动半径即地球半径,故其向心加速度最大;在两极,其转动半径为零,所以其向心加速度也为零;随着纬度的升高,其转动半径减小,故其向心加速度也减小.正确选项为A、D.
答案 AD
图2-2-13
9.在光滑的水平面上相距40 cm的两个钉子A和B,如图2-2-13所示,长1 m的细绳一端系着质量为0.4 kg的小球,另一端固定在钉子A上,开始时,小球和钉子A、B在同一直线上,小球始终以2 m/s的速率在水平面上做匀速圆周运动.若细绳能承受的最大拉力是4 N,那么,从开始到细绳断开所经历的时间是 ( ).
A.0.9π s B.0.8π s
C.1.2π s D.1.6π s
解析 当小球绕A以1 m的半径转半圈的过程中,拉力F1=m=0.4× N=1.6 N,绳不断;
当小球继续绕B以0.6 m的半径转半圈的过程中,拉力F2=m=2.67 N,绳不断
当小球再碰到钉子A,将以半径0.2 m做圆周运动,拉力F3=m=8 N,绳断;
所以,在绳断之前小球转过两个半圈,时间分别为
t1=== s=0.5π s,
t2=== s=0.3π s
所以,断开前总时间是t=t1+t2=0.8π s.
答案 B
图2-2-14
10.如图2-2-14所示,质量相等的小球A、B分别固定在轻杆的中点及端点,当杆在光滑的水平面上绕O点匀速转动时,求杆的OA段及AB段对球的拉力大小之比.
解析 隔离A、B受力分析,如下图所示.由于A、B放在水平面上,故G=N,又由A、B固定在同一根轻杆上,所以A、B的角速度相同,设角速度为ω,则由向心力公式可得:
对A:FOA-FBA=mrω2
对B:FAB=m·2rω2,而FBA=FAB
联立以上三式得FOA∶FAB=3∶2.
答案 3∶2
图2-2-15
11.如图2-2-15所示,有一质量为m
的小球在光滑的半球形碗内做匀速圆周运动,轨道平面在水平面内.已知小球与半球形碗的球心O的连线跟竖直方向的夹角为θ,半球形碗的半径为R,求小球做圆周运动的速度及碗壁对小球的弹力各多大.
解析 根据小球做圆周运动的轨迹找圆心,定半径,由题图可知,圆周运动的圆心为O′,运动半径为r=Rsin θ.小球受重力mg及碗对小球弹力N的作用,向心力为弹力的水平分力.受力分析如右图所示.
由向心力公式Fn=m得Nsin θ=m ①
竖直方向上小球的加速度为零,所以竖直方向上所受的合力为零,即Ncos θ=mg,解得N= ②
联立①②两式,可解得物体做匀速圆周运动的速度为
v=.
答案
12.如图2-2-16所示,细绳一端系着质量为M=0.6 kg的物体,静止在水平盘面上,另一端通过光滑小孔吊着质量m=0.3 kg的物体,M的中心与小孔距离为0.2 m,并知M和水平盘面的最大静摩擦力为2 N.现使此水平盘绕中心轴转动,
图2-2-16
问角速度ω在什么范围内m处于静止状态?(g取10 m/s2)
解析 设物体M和水平盘面保持相对静止,当ω具有最小值时,M有向着圆心O运动的趋势,故水平盘面对M的摩擦力方向背向圆心,且等于最大静摩擦力fmax=2 N.
对于M:F-fmax=Mrω,则ω1= =
= rad/s≈2.9 rad/s.
当ω具有最大值时,M有离开圆心O的趋势,水平盘面对M摩擦力的方向指向圆心,fmax=2 N.
对M有:F+fmax=Mrω
则ω2= = ≈6.5 rad/s,
故ω的范围是2.9 rad/s≤ω≤6.5 rad/s.
答案 2.9 rad/s≤ω≤6.5 rad/s