- 2021-05-26 发布 |
- 37.5 KB |
- 55页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021高考物理二轮复习专题一力和运动第2讲力与直线运动课件
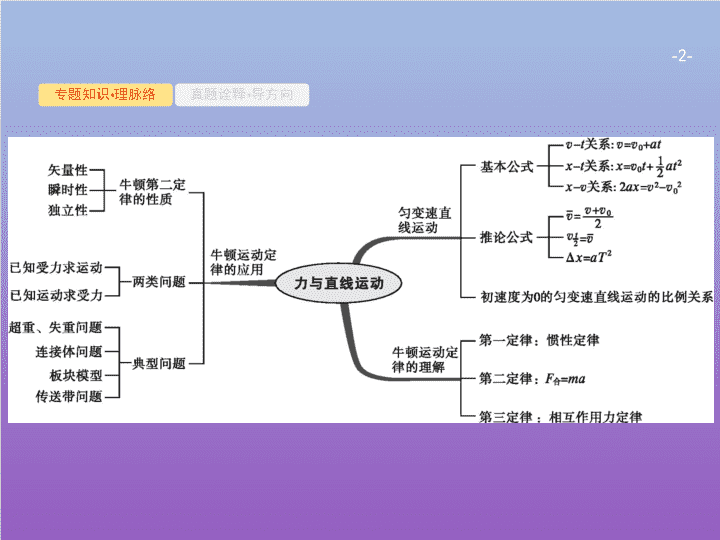
第 2 讲 力与直线运动 - 2 - 专题知识 • 理脉络 真题诠释 • 导方向 - 3 - 专题知识 • 理脉络 真题诠释 • 导方向 1 . (2019· 浙江卷 ) 甲、乙两物体零时刻开始从同一地点向同一方向做直线运动 , 位移 — 时间图像如图所示 , 则在 0 ~t 1 时间内 ( ) A. 甲的速度总比乙大 B. 甲、乙位移相同 C. 甲经过的路程比乙小 D. 甲、乙均做加速运动 B 解析 : 在位移 — 时间图像中 , 斜率表示速度 , 在 t 1 时刻 , 乙的斜率大于甲的斜率 , 乙的速度大于甲的速度 ,A 错误 ; 在位移 — 时间图像中 , 位移就是两时刻的坐标差 ,0 ~t 1 时间内 , 甲和乙的坐标差相等 ,B 正确 ; 斜率始终为正数 , 表明速度始终沿着正方向做直线运动 , 位移等于路程 , 甲和乙的路程相等 ,C 错误 ; 甲的斜率不变 , 甲做匀速运动 ,D 错误。 - 4 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 匀变速直线运动的图像。 能力要求 本题考查对位移图像的物理意义的理解 , 只要抓住纵坐标表示物体的位置 , 纵坐标的变化量等于物体的位移 , 斜率等于速度 , 就能 分析两 物体的运动情况。 - 5 - 专题知识 • 理脉络 真题诠释 • 导方向 2 . ( 多选 )(2016· 天津卷 ) 我国高铁技术处于世界领先水平。和谐号动车组是由动车和拖车编组而成 , 提供动力的车厢叫动车 , 不提供动力的车厢叫拖车。假设动车组各车厢质量均相等 , 动车的额定功率都相同 , 动车组在水平直轨道上运行过程中阻力与车重成正比。某列动车组由 8 节车厢组成 , 其中第 1 、 5 节车厢为动车 , 其余为拖车 , 则该动车组 ( ) A. 启动时乘客受到车厢作用力的 方向 与 车运动的方向相反 B. 做匀加速运动时 , 第 5 、 6 节与第 6 、 7 节 车厢间的作用力之比为 3 ∶ 2 C. 进站时从关闭发动机到停下来滑行的距离与关闭发动机时的速度成正比 D. 与改为 4 节动车带 4 节拖车的动车组最大速度之比为 1 ∶ 2 BD - 6 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : 设每节车厢质量为 m , 由题意可知 , 动车组所受阻力 F f =k· 8 mg , k 为比例系数。启动时 , 乘客随车一起向前做加速运动 , 水平方向由 F=m 人 a 知乘客所受到车厢作用力的方向与车运动方向相同 , 竖直方向受到重力和支持力 , 则乘客受到车厢作用力应沿前进方向斜向上 , 选项 A 错误 ; 做匀加速运动时 , 设总动力为 F , 则 F-k· 8 mg= 8 ma , 设第 5 、 6 节车厢之间的作用力为 F 1 , 以 “6 、 7 、 8” 三节车厢为研究对象 , 得 确 ; 进站时从关闭发动机到停下来 , 水平方向上只受阻力 , a'=kg , 由 0 -v 2 =- 2 ·a'·x 知 , 滑行距离与速度的二次方成正比 , 选项 C 错误 ;2 节动车 ,2 P=k· 8 mg·v m1 ,4 节动车 ,4 P=k· 8 mg·v m2 , 解得 v m1 ∶ v m2 = 1 ∶ 2, 故选项 D 正确。 - 7 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 牛顿运动定律、功率、动能定理。 能力要求 能应用整体法与隔离法 分析连接体 问题 , 恰当选取研究 对象 分析 动力学 与能量问题。 - 8 - 专题知识 • 理脉络 真题诠释 • 导方向 3 . ( 多选 )(2019· 全国卷 3) 如图甲所示 , 物块和木板叠放在实验台上 , 物块用一不可伸长的细绳与固定在实验台上的力传感器相连 , 细绳水平。 t= 0 时 , 木板开始受到水平外力 F 的作用 , 在 t= 4 s 时撤去外力。细绳对物块的拉力 F' 随时间 t 变化的关系如图乙所示 , 木板的速度 v 与时间 t 的关系如图丙所示。木板与实验台之间的摩擦可以忽略。重力加速度取 10 m/s 2 。由题给数据可以得出 ( ) - 9 - 专题知识 • 理脉络 真题诠释 • 导方向 A. 木板的质量为 1 kg B.2 ~ 4 s 内 , 力 F 的大小为 0 . 4 N C.0 ~ 2 s 内 , 力 F 的大小保持不变 D. 物块与木板之间的动摩擦因数为 0 . 2 答案 : AB 解析 : 对物块受力分析可知 , 细绳对物块的拉力 F' 等于木板与物块间的摩擦力。由题图乙可知 , 滑动摩擦力 F f = 0 . 2 N, 设木板质量为 m 木 , m 木 = 1 kg,A 正确。对木板 :2 ~ 4 s 内 , F-F f =m 木 a 1 , a 1 = 0 . 2 m/s 2 , 求得 F= 0 . 4 N,B 正确。对木板 :0 ~ 2 s, 拉力 F 与静摩擦力 F f 静 平衡 , F=F f 静 =kt ,C 错误。物块质量未知 , 无法求正压力 , 无法求动摩擦因数 μ ,D 错误。 - 10 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 牛顿运动定律的综合应用。 能力要求 关键是弄清楚物体的运动过程和受力情况 , 利用牛顿第二定律或运动学的计算公式求解加速度 , 再根据题目要求进行 解答。 - 11 - 专题知识 • 理脉络 真题诠释 • 导方向 4 . (2018· 天津卷 ) 我国自行研制、具有完全自主知识产权的新一代大型喷气式客机 C919 首飞成功后 , 拉开了全面试验试飞的新征程。假设飞机在水平跑道上的滑跑是初速度为零的匀加速直线运动 , 当位移 x= 1 . 6×10 3 m 时才能达到起飞所要求的速度 v= 80 m/s 。已知飞机质量 m= 7 . 0×10 4 kg, 滑跑时受到的阻力为自身重力 的 , 重力加速度 g 取 10 m/s 2 。求飞机滑跑过程中 : (1) 加速度 a 的大小 ; (2) 牵引力的平均功率 P 。 - 12 - 专题知识 • 理脉络 真题诠释 • 导方向 答案 : (1)2 m/s 2 (2)8 . 4×10 6 W 解析 : (1) 飞机滑跑过程中做初速度为零的匀加速直线运动 , 有 v 2 = 2 ax ① 代入数据解 得 a= 2 m/s 2 。 ② (2) 设飞机滑跑受到的阻力为 F 阻 , 依题意有 F 阻 = 0 . 1 mg ③ 设发动机的牵引力为 F , 根据牛顿第二定律有 F-F 阻 =ma ④ 联立 ②③④⑤⑥ 式得 P= 8 . 4×10 6 W 。 ⑦ - 13 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 牛顿运动定律 , 匀变速直线运动。 能力要求 分析运动 过程与受力情况 , 根据运动规律与牛顿运动 定律 分析 。 - 14 - 突破点一 突破点二 突破点三 突破点四 突破点五 匀变速直线运动规律的应用 考查方向 常以选择题或计算题的形式考查。 突破方略 1 . 牢记解决匀变速直线运动问题的五种常用方法 逆向思维法 → 匀减速直线运动可视为反方向的匀加速直线运动 比例法 → 适用于初速度为 0 或末速度为 0 的匀变速直线运动 - 15 - 突破点一 突破点二 突破点三 突破点四 突破点五 2 . 处理刹车类问题的思路 先判断刹车时间 , 再进行 分析计算 。 - 16 - 突破点一 突破点二 突破点三 突破点四 突破点五 模型构建 【例 1 】 (2019· 山东六校联考 ) 某高速公路同一直线车道上同向匀速行驶的轿车和货车 , 其速度大小分别为 v 1 = 30 m/s 、 v 2 = 20 m/s, 轿车与前方货车间距离 x 0 = 12 m 时轿车司机才发现货车 , 若此时轿车立即刹车 , 则轿车要经过 x= 112 . 5 m 的匀减速直线运动才能停下来。两车均可视为质点 , 忽略轿车司机的反应时间。 (1) 若轿车刹车时货车以速度 v 2 匀速行驶 , 通过计算 分析两 车是否会相撞 ; (2) 若轿车在刹车的同时给货车发信号 , 货车司机经 t 0 = 1 s 收到信号并立即以大小 a 0 = 2 m/s 2 的加速度匀加速行驶 , 通过 计算 分析 两 车是否会相撞。 - 17 - 突破点一 突破点二 突破点三 突破点四 突破点五 分析推理 (1) 匀减速直线运动追匀速直线运动 , 速度相等时若未相撞 , 以后还会相撞吗 ? (2) 货车司机在反应时间内做什么运动 ? (1) 提示 : 不会。 (2) 提示 : 仍以原来速度做匀速直线运动 。 - 18 - 突破点一 突破点二 突破点三 突破点四 突破点五 答案 : (1) 会相撞 (2) 不会相撞 解析 : (1) 轿车经过 x= 112 . 5 m 才能停下来 , 可得轿车刹车过程的加速度大小 a 1 = 4 m/s 2 恰好不相撞时两车速度相等 , 即 v 1 -a 1 t=v 2 货车前进的距离 x 2 =v 2 t= 50 m 因为 x 1 >x 2 +x 0 , 所以两车相撞。 - 19 - 突破点一 突破点二 突破点三 突破点四 突破点五 (2) 设经历时间 t' 两车的速度相等 则 v 1 -a 1 t'=v 2 +a 0 ( t'-t 0 ) 此过程中轿车前进的距离 解得 x 1 '= 52 m, x 2 '= 41 m 因 x 1 '-x 2 '= 11 m查看更多