【物理】2019届一轮复习人教版 　机械振动 学案

【物理】2019届一轮复习人教版 　机械振动 学案

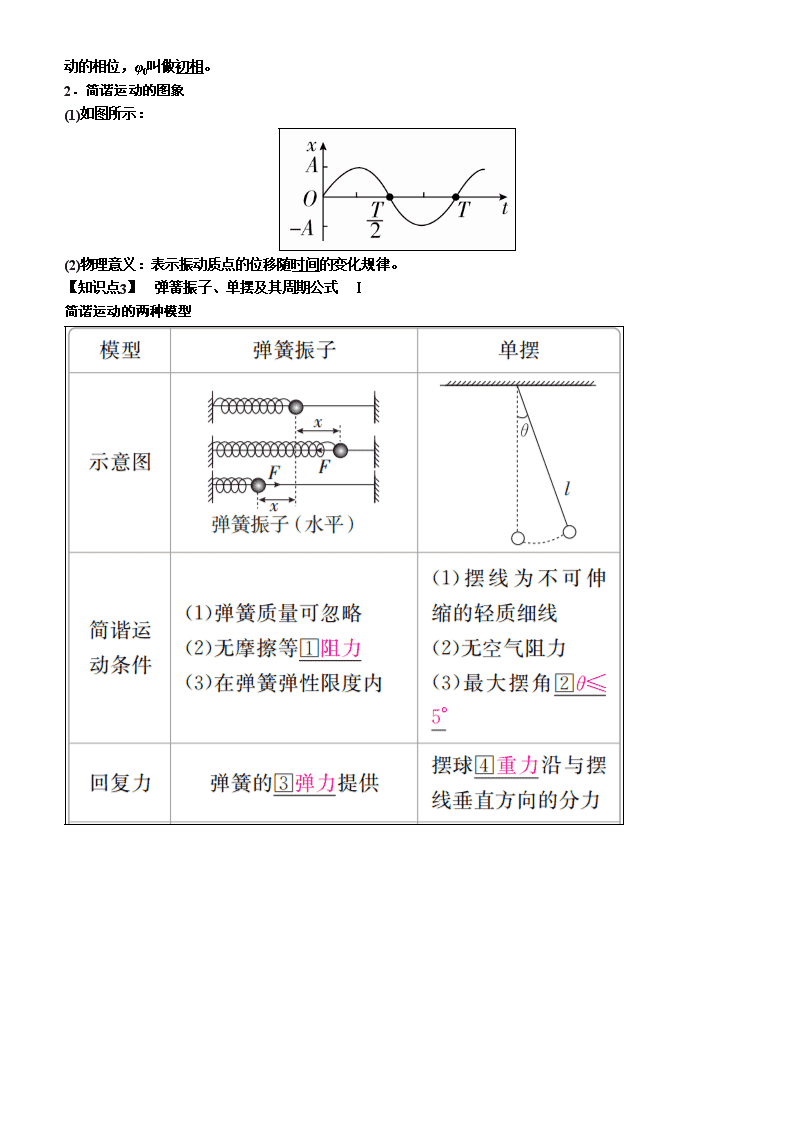
第 1 讲　机械振动 板块一　主干梳理·夯实基础 【知识点 1】　简谐运动　Ⅰ 1．简谐运动的概念 质点的位移与时间的关系遵从正弦函数的规律，即它的振动图象(x­t 图象)是一条正弦曲线。 2．平衡位置 物体在振动过程中回复力为零的位置。 3．回复力 (1)定义：使物体返回到平衡位置的力。 (2)方向：总是指向平衡位置。 (3)来源：属于效果力，可以是某一个力，也可以是几个力的合力或某个力的分力。 4．描述简谐运动的物理量 【知识点 2】　简谐运动的公式和图象　Ⅱ 1．表达式 (1)动力学表达式：F＝－kx，其中“－”表示回复力与位移的方向相反。 (2)运动学表达式：x＝Asin(ωt＋φ0)，其中 A 代表振幅，ω＝2π T ＝2πf 表示简谐运动的快慢，ωt＋φ0 代表简谐运 动的相位，φ0 叫做初相。 2．简谐运动的图象 (1)如图所示： (2)物理意义：表示振动质点的位移随时间的变化规律。 【知识点 3】　弹簧振子、单摆及其周期公式　Ⅰ 简谐运动的两种模型 【知识点 4】　受迫振动和共振　Ⅰ 1．自由振动、受迫振动和共振的比较 2．共振曲线 如图所示的共振曲线，曲线表示受迫振动的振幅 A(纵坐标)随驱动力频率 f(横坐标)的变化而变化。驱动力的 频率 f 跟振动系统的固有频率 f0 相差越小，振幅越大；驱动力的频率 f 等于振动系统的固有频率 f0 时，振幅最 大。 【知识点 5】　实验：用单摆测定重力加速度 1.实验原理 由单摆的周期公式 T＝2π l g，可得出 g＝4π2 T2 l，测出单摆的摆长 l 和振动周期 T，就可求出当地的重力加速度 g。 2．实验器材 带中心孔的小钢球、约 1 m 长的细线、带有铁夹的铁架台、游标卡尺、毫米刻度尺、停表。 3．实验步骤 (1)做单摆 取约 1 m 长的细线穿过带中心孔的小钢球，并打一个比小孔大一些的结，然后把线的另一端用铁夹固定在铁 架台上，让摆球自然下垂，如图所示。 (2)测摆长 用毫米刻度尺量出摆线长 L(精确到毫米)，用游标卡尺测出小球直径 D，则单摆的摆长 l＝L＋D 2。 (3)测周期 将单摆从平衡位置拉开一个角度(小于 5°)，然后释放小球，记下单摆摆动 30～50 次全振动的总时间，算出平 均每摆动一次的时间，即为单摆的振动周期。 (4)改变摆长，重做几次实验。 (5)数据处理 ①公式法：g＝4π2l T2 。 ②图象法：画 l­T2 图象。 g＝4π2k，k＝ l T2＝ Δl ΔT2。 4．注意事项 (1)悬线顶端不能晃动，需用夹子夹住，保证悬点固定。 (2)单摆必须在同一平面内振动，且摆角小于 10°。 (3)选择在摆球摆到平衡位置处时开始计时，并数准全振动的次数。 (4)小球自然下垂时，用毫米刻度尺量出悬线长 L，用游标卡尺测量小球的直径，然后算出摆球的半径 r，则摆 长 l＝L＋r。 (5)选用 1 m 左右难以伸缩的细线。 板块二　考点细研·悟法培优　　　　　　　　　　　　　　　　　 考点 1 简谐运动的五个特征[深化理解] 1．动力学特征 F＝－kx，“－”表示回复力的方向与位移方向相反，k 是比例系数，不一定是弹簧的劲度系数。 2．运动学特征 做简谐运动的物体加速度与物体偏离平衡位置的位移大小成正比而方向相反，为变加速运动，远离平衡位置 时，x、F、a、Ep 均增大，v、Ek 均减小，靠近平衡位置时则相反。 3．运动的周期性特征 相隔 T 或 nT 的两个时刻，物体处于同一位置且振动状态相同。 4．对称性特征 (1)时间对称性：相隔T 2或 (2n＋1)T 2 (n 为正整数)的两个时刻，物体位置关于平衡位置对称，位移、速度、加速 度大小相等，方向相反。如图所示： O 为平衡位置，A、B 为振子偏离平衡位置最大位移处，振子 t 时刻在 C 点，t＋ (2n＋1)T 2 时刻运动到 D 点，则 位移 xD＝－xC，速度 vD＝－vC，aD＝－aC。 (2)空间对称性：如图所示，振子经过关于平衡位置 O 对称的两点 P、P′(OP＝OP′)时，速度的大小、动能、 势能相等，相对于平衡位置的位移大小相等。 此外，振子由 P 到 O 所用时间等于由 O 到 P′所用时间，即 tPO＝tOP′。振子往复过程中通过同一段路程(如 OP 段)所用时间相等，即 tOP＝tPO。 5．能量特征 振动的能量包括动能 Ek 和势能 Ep，简谐运动过程中，系统动能与势能相互转化，系统的机械能守恒。 例 1　(多选)如图所示，一个质点在平衡位置 O 点附近做机械振动。若从 O 点开始计时，经过 3 s 质点第一次 经过 M 点，继续运动，又经过 2 s 它第二次经过 M 点，则该质点第三次经过 M 点还需要的时间是(　　) A．8 s B．4 s C．14 s D.10 3 s (1)连续经过相同位置时的两个不同时刻，相同的量是什么？不同的量是什么？ 提示：相同的量：位移、回复力、加速度、动能、弹性势能； 不同的量：速度(大小相等，方向相反)。 (2)从第一次经过 M 点到第三次经过 M 点是多长时间？ 提示：一个周期。 尝试解答　选 CD。 如图所示，设 a、b 两点为质点振动过程的最大位移处，若开始计时时刻，质点从 O 点向右运动，O→M 过程 历时 3 s，M→b→M 运动过程历时 2 s，显然，T 4＝4 s，T＝16 s。质点第三次经过 M 点还需要的时间 Δt3＝T－ 2 s＝14 s，C 正确。若开始计时时刻，质点从 O 点向左运动，O→a→O→M 运动过程历时 3 s，M→b→M 运动 过程历时 2 s，显然，T′ 2 ＋T′ 4 ＝4 s，T′＝16 3 s。质点第三次经过 M 点还需要的时间 Δt3′＝T－2 s＝10 3 s， D 正确。 总结升华 分析简谐运动的技巧 (1)分析简谐运动中各物理量的变化情况时，要以位移为桥梁，位移增大时，振动质点的回复力、加速度、势 能均增大，速度、动能均减小；反之，则产生相反的变化。另外，各矢量均在其值为零时改变方向。 (2)分析过程中要特别注意简谐运动的周期性和对称性。 (3)如上例，若没有给出开始时刻质点的振动方向，还须分情况讨论，以防丢解。 [跟踪训练]　如图所示，弹簧振子在 BC 间振动，O 为平衡位置，BO＝OC＝5 cm，若振子从 B 到 C 的运动时 间是 1 s，则下列说法中正确的是 (　　) A．振子从 B 经 O 到 C 完成一次全振动 B．振动周期是 1 s，振幅是 10 cm C．经过两次全振动，振子通过的路程是 20 cm D．从 B 开始经过 3 s，振子通过的路程是 30 cm 答案　D 解析　振子从 B→O→C 仅完成了半次全振动，所以周期 T＝2×1 s＝2 s，振幅 A＝BO＝5 cm，A、B 错误； 振子在一次全振动中通过的路程为 4A＝20 cm，所以两次全振动中通过的路程为 40 cm，C 错误；3 s 的时间 为 1.5T，振子通过的路程为 30 cm，D 正确。 考点 2 简谐运动的图象[拓展延伸] 1．图象特征 (1)简谐运动的图象是一条正弦或余弦曲线，是正弦曲线还是余弦曲线取决于质点初始时刻的位置。 (2)图象反映的是位移随时间的变化规律，随时间的增加而延伸，图象不代表质点运动的轨迹。 (3)任一时刻在图线上对应点的切线的斜率，大小表示该时刻振子的速度大小，正负表示速度的方向，为正时， 表示振子的速度沿 x 轴正方向；为负时，表示振子的速度沿 x 轴负方向。 2.图象信息 (1)由图象可以看出质点振动的振幅、周期。 (2)可以确定某时刻质点离开平衡位置的位移。 (3)可以确定某时刻质点的回复力、加速度和速度的方向。 ①回复力和加速度的方向：因回复力总是指向平衡位置，故回复力和加速度的方向在图象上总是指向 t 轴。 ②速度的方向：某时刻速度的方向既可以通过该时刻在图象上对应点的切线的斜率来判断，还可以通过下一 时刻位移的变化来判断，若下一时刻位移增加，速度方向就是远离 t 轴；若下一时刻位移减小，速度方向就是 指向 t 轴。 (4)可以确定某段时间质点的位移、回复力、加速度、速度、动能、势能等的变化情况。 例 2　一质点做简谐运动，其位移和时间的关系如图所示。 (1)求 t＝0.25×10－2 s 时质点偏离平衡位置的位移； (2)在 t＝1.5×10－2 s 到 t＝2×10－2 s 这段时间，质点的位移、回复力、速度、动能、势能如何变化？ (3)在 t＝0 到 t＝8.5×10－2 s 这段时间，质点运动的路程、位移各是多少？ (1)如何确定图象上某一时刻质点的速度、加速度？ 提示：下一时刻位移增加，速度方向远离时间轴，质点向背离平衡位置方向运动；反之，向朝向平衡位置方向 运动。加速度方向永远指向时间轴，指向平衡位置。 (2)从 t＝0 到 t＝1×10－2 s 时间内，质点速度大小如何变化？图象上斜率表示什么？ 提示：速度先增大后减小；图象上斜率表示速度。 尝试解答　(1)x＝－ 2 cm　(2)位移变大，回复力变大，速度变小，动能变小，势能变大　(3)s 路程＝34 cm　x 位移＝2 cm，方向沿正方向。 (1)由题图可知 A＝2 cm，T＝2×10 －2 s，振动方程为 x＝Asin(ωt－π 2)＝－Acosωt＝－2cos 2π 2 × 10－2t cm＝－ 2cos100πt cm，当 t＝0.25×10－2 s 时，x＝－ 2 cm。 (2)由题图可知在 1.5×10－2 s 到 2×10－2 s 这段时间，质点的位移变大，回复力变大，速度变小，动能变小， 势能变大。 (3)从 t＝0 到 t＝8.5×10－2 s 这段时间等于质点做简谐运动的17 4 个周期，质点运动的路程为 s 路程＝17A＝34 cm， 位移为 x 位移＝2 cm，方向沿正方向。 总结升华 对振动图象的理解 (1)可确定振动质点在任一时刻的位移。如图所示，t1、t2 时刻质点偏离平衡位置的位移分别为 x1＝7 cm，x2＝－ 5 cm。 (2)可确定质点振动的振幅，图象中最大位移的绝对值就是质点振动的振幅。如图所示，质点振动的振幅是 10 cm。 (3)可确定质点振动的周期和频率，振动图象上一个完整的正弦(或余弦)图形在时间轴上拉开的“长度”表示周 期，频率的大小等于周期的倒数。如图所示，OD、AE、BF 的间隔都等于质点振动的周期，T＝0.2 s，频率 f＝ 1 T＝5 Hz。 (4)可确定质点的振动方向。如图所示，在 t1 时刻，质点正远离平衡位置向正方向运动；在 t3 时刻，质点正朝 向平衡位置运动。 (5)可比较各时刻质点加速度的大小和方向。例如在图中 t1 时刻，质点偏离平衡位置的位移 x1 为正，则加速度 a1 为负；在 t2 时刻，质点偏离平衡位置的位移 x2 为负，则加速度 a2 为正，因为|x1|>|x2|，所以|a1|>|a2|。 [跟踪训练]　[2017·茂名模拟](多选)简谐运动的振动图象可用下述方法画出：如图甲所示，在弹簧振子的小球 上安装一支绘图笔 P，让一条纸带在与小球振动方向垂直的方向上匀速运动，笔 P 在纸带上画出的就是小球 的振动图象。取水平向右为小球离开平衡位置位移的正方向，纸带运动的距离代表时间，得到的弹簧振子振 动图象如图乙所示。则下列说法正确的是(　　) A．弹簧振子的周期为 4 s B．弹簧振子的振幅为 10 cm C．t＝17 s 时振子相对平衡位置的位移是 10 cm D．若纸带运动的速度为 2 cm/s，振动图线上 1、3 两点间的距离是 4 cm E．t＝2.5 s 时振子正在向 x 轴正方向运动 答案　ABD 解析　由题图知，弹簧振子的周期为 T＝4 s，振幅为 10 cm，选项 A、B 正确；由简谐运动的周期性知，t＝17 s 时振子相对平衡位置的位移与 t＝1 s 时振子相对平衡位置的位移相同，均为 0，选项 C 错误；若纸带运动的 速度为 2 cm/s，振动图线上 1、3 两点间的距离 s＝vt＝2 cm/s×2 s＝4 cm，选项 D 正确；x­t 图象的斜率表示 速度，斜率的正负表示速度的方向，由题图可知，t＝2.5 s 时振子的速度为负值，故振子正在向 x 轴负方向运 动，选项 E 错误。 考点 3 用单摆测重力加速度[解题技巧] 1．对单摆的理解 单摆是一个理想化模型，摆角 θ≤5°时，单摆的周期为 T＝2π l g，与单摆的振幅 A、摆球质量 m 无关，式中 的 g 由单摆所处的位置决定。 2．等效摆长及等效重力加速度 (1)l′——等效摆长：摆动圆弧的圆心到摆球重心的距离。如图甲所示的双线摆的摆长 l′＝r＋Lcosα。乙图 中小球(可看作质点)在半径为 R 的光滑圆槽中靠近 A 点的附近振动，其等效摆长为 l′＝R。 (2)g′——等效重力加速度：与单摆所处物理环境有关。 ①在不同星球表面：g′＝GM R2 ，M 为星球的质量，R 为星球的半径； ②单摆处于超重或失重状态下的等效重力加速度分别为 g′＝g＋a 和 g′＝g－a，a 为超重或失重时单摆系统 整体竖直向上或竖直向下的加速度大小。 3．用单摆测重力加速度实验 数据处理的两种方法： 方法一：公式法。 根据公式 T＝2π l g，g＝4π2l T2 。将测得的几组周期 T 和摆长 l 分别代入公式 g＝4π2l T2 中算出多组重力加速度 g 的值，再求出 g 的平均值，即为当地重力加速度的值。 方法二：图象法。 由单摆的周期公式 T＝2π l g可得 l＝ g 4π2T2，因此以摆长 l 为纵轴，以 T2 为横轴描点、作图，作出的 l­T2 图象 理论上是一条过原点的直线，如图所示，求出图象的斜率 k，即可求出 g 值。g＝4π2k，k＝ l T2＝ Δl ΔT2。 例 3　根据单摆周期公式 T＝2π l g，可以通过实验测量当地的重力加速度。如图甲所示，将细线的上端固定 在铁架台上，下端系一小钢球，就做成了单摆。 (1)用游标卡尺测量小钢球直径，示数如图乙所示，读数为________mm。 (2)以下是实验过程中的一些做法，其中正确的有________。 a．摆线要选择较细、伸缩性较小，并且尽可能长一些的 b．摆球尽量选择质量较大、体积较小的 c．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆线相对平衡位置时有较大的偏角 d．拉开摆球，使摆线偏离平衡位置的夹角不大于 5°，在释放摆球的同时开始计时，当摆球回到起始位置时停 止计时，此时间间隔 Δt 即为单摆周期 T e．拉开摆球，使摆线偏离平衡位置的夹角不大于 5°，释放摆球，当摆球振动稳定后，从平衡位置开始计时， 记下摆球做 50 次全振动所用的时间 Δt，则单摆周期 T＝Δt 50 (1)关于单摆摆线的长度及悬点有何要求？ 提示：单摆摆线的长度应远大于摆球的直径；悬点必须固定。 (2)游标卡尺应当怎样读数？ 提示：游标卡尺的读数 L＝L0＋kn，其中 L0 为主尺上对应的刻度，即副尺“0”刻度线以左的刻度，k 为副尺的 精确度，n 为与主尺上刻线对齐的副尺上的刻线对应的刻度数。 (3)单摆的摆角及计时有何要求？ 提示：单摆的摆角即摆线与竖直方向的夹角应不大于 5°；为减小误差，当摆球经过平衡位置时开始计时。 尝试解答　(1)18.5__(2)abe。 (1)如题中图乙所示，主尺上对应的刻度为 18 mm，副尺的精度为 1 10 mm＝0.1 mm，与主尺上刻线对齐的副尺 上的刻线对应的刻度数是 5，所以游标卡尺读数为 18 mm＋5×0.1 mm＝18.5 mm。 (2)摆线细一些有助于减小空气阻力，伸缩性小一些可使摆线长度较稳定，尽可能长一些可使单摆周期较大， 方便周期的测量，故 a 正确。摆球质量大一些，体积小一些能减小空气阻力对实验的影响，故 b 正确。根据 T ＝2π l g可知，单摆周期 T 与振幅无关，且摆角太大时，单摆的运动不能看作简谐运动，不符合实验要求，故 c 错误。测量周期时应从小球经过平衡位置即最低点位置时开始计时，而且应记录 n 次全振动的时间 Δt，则 T ＝Δt n ，故 d 错误，e 正确。 总结升华 用单摆测重力加速度实验的误差分析 (1)本实验的系统误差主要来源于单摆模型本身是否符合要求，即：悬点固定，小球质量大、体积小，细线轻 质非弹性，振动是在同一竖直平面内的振动，这些要求是否符合。 (2)本实验的偶然误差主要来自时间的测量，因此，要从摆球通过平衡位置时开始计时，不能多计或漏计摆球 全振动次数。此外，使用刻度尺测量摆线长度读数时也会产生偶然误差。 (3)利用图象法处理数据具有形象、直观的特点，同时也能减小实验误差。利用图象法分析处理时要特别注意 图象的斜率及截距的物理意义。 [跟踪训练]　某同学在“用单摆测定重力加速度”的实验中进行了如下的操作： (1)用游标尺上有 10 个小格的游标卡尺测量摆球的直径，得到如图甲所示结果，则可读出摆球的直径为 ________cm。把摆球用细线悬挂在铁架台上，测量摆线长，通过计算得到摆长 L。 (2)用秒表测量单摆的周期，当单摆摆动稳定且到达最低点时开始计时并记为 n＝1，单摆每经过最低点计一次 数，当数到 n＝60 时秒表的示数如图乙所示，该单摆的周期是 T＝________s(结果保留三位有效数字)。 (3)测量出多组周期 T、摆长 L 的数值后，画出 T2­L 图象如图丙所示，此图象斜率的物理意义是 (　　) A．g B.1 g C.4π2 g D. g 4π2 (4)在(3)中，描点时若误将摆线长当作摆长，那么画出的直线将不通过原点，由图象斜率得到的重力加速度与 原来相比，其大小 (　　) A．偏大 B．偏小 C．不变 D．都有可能 (5)该小组的另一同学没有使用游标卡尺也测出了重力加速度，他采用的方法是：先测出一摆线较长的单摆的 振动周期 T1，然后把摆线缩短适当的长度 ΔL，再测出其振动周期 T2。用该同学测出的物理量表示重力加速 度，则 g＝________。 答案　(1)2.06　(2)2.28　(3)C　(4)C　(5) 4π2ΔL T21－T22 解析　(1)摆球的直径为 d＝20 mm＋6× 1 10 mm＝20.6 mm＝2.06 cm。 (2)秒表的读数为 t＝60 s＋7.4 s＝67.4 s，根据题意 t＝60－1 2 T＝59 2 T，所以周期 T＝2t 59≈2.28 s。 (3)根据单摆周期公式 T＝2π L g，可得T2 L ＝4π2 g ＝k(常数)，所以选项 C 正确。 (4)因为T2 L ＝4π2 g ＝k，(常数)，所以ΔT2 ΔL ＝4π2 g ＝k，若误将摆线长当作摆长，画出的直线将不通过原点，但图象 的斜率仍然满足T21－T22 L1－L2＝ΔT2 ΔL ＝4π2 g ＝k，所以由图象的斜率得到的重力加速度不变。 (5)根据(4)的分析，ΔT2 ΔL ＝4π2 g ，所以 g＝4π2ΔL ΔT2 ＝4π2ΔL T21－T22。