- 2021-05-26 发布 |
- 37.5 KB |
- 32页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2019届二轮磁场学案(全国通用)
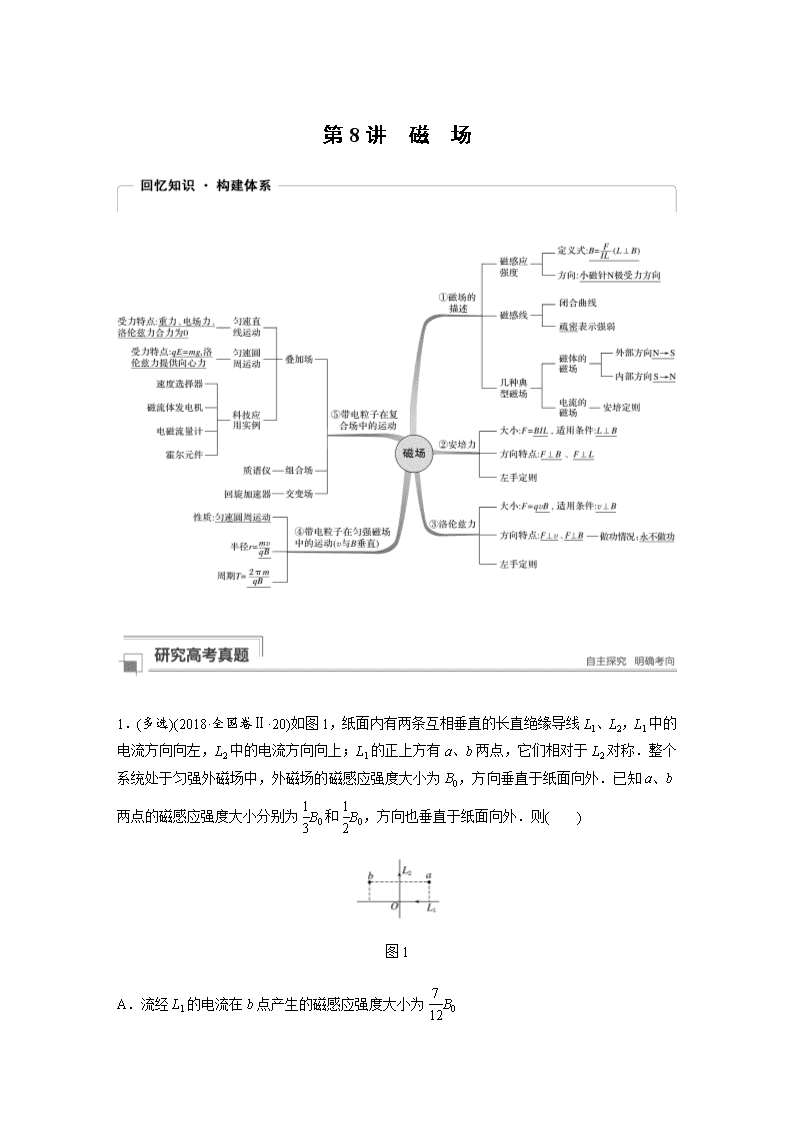
第8讲 磁 场 1.(多选)(2018·全国卷Ⅱ·20)如图1,纸面内有两条互相垂直的长直绝缘导线L1、L2,L1中的电流方向向左,L2中的电流方向向上;L1的正上方有a、b两点,它们相对于L2对称.整个系统处于匀强外磁场中,外磁场的磁感应强度大小为B0,方向垂直于纸面向外.已知a、b两点的磁感应强度大小分别为B0和B0,方向也垂直于纸面向外.则( ) 图1 A.流经L1的电流在b点产生的磁感应强度大小为B0 B.流经L1的电流在a点产生的磁感应强度大小为B0 C.流经L2的电流在b点产生的磁感应强度大小为B0 D.流经L2的电流在a点产生的磁感应强度大小为B0 【考点定位】 磁场的叠加、安培定则 【点评】 2017、2018这两年对磁场叠加连续考察,但难度不大,主要考查安培定则、平行四边形定则及电流的磁场、磁感线分布特点 【难度】 较易 答案 AC 解析 原磁场、电流的磁场方向如图所示, 由题意知在b点: B0=B0-B1+B2 在a点:B0=B0-B1-B2 由上述两式解得B1=B0,B2=B0,A、C项正确. 2.(2017·全国卷Ⅰ·16)如图2所示,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向里,三个带正电的微粒a、b、c电荷量相等,质量分别为ma、mb、mc,已知在该区域内,a在纸面内做匀速圆周运动,b在纸面内向右做匀速直线运动,c在纸面内向左做匀速直线运动.下列选项正确的是( ) 图2 A.ma>mb>mc B.mb>ma>mc C.mc>ma>mb D.mc>mb>ma 【考点定位】 带电物体在复合场中的运动、受力分析 【难度】 中等 答案 B 解析 设三个微粒的电荷量均为q, a在纸面内做匀速圆周运动,说明洛伦兹力提供向心力,重力与电场力平衡,即 mag=qE① b在纸面内向右做匀速直线运动,三力平衡,则 mbg=qE+qvB② c在纸面内向左做匀速直线运动,三力平衡,则 mcg+qvB=qE③ 比较①②③式得:mb>ma>mc,选项B正确. 3.(2017·全国卷Ⅱ·18)如图3所示,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同的方向射入磁场,若粒子射入速率为v1,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为v2,相应的出射点分布在三分之一圆周上,不计重力及带电粒子之间的相互作用,则v2∶v1 为( ) 图3 A.∶2 B.∶1 C.∶1 D.3∶ 【考点定位】 带电粒子在有界磁场中的运动 【点评】 全国卷中带电粒子在匀强磁场中的运动一般在选择题中考察,情景一般较新,有一定难度. 【难度】 较难 答案 C 解析 当粒子在磁场中运动半个圆周时,打到圆形磁场边界的位置距P点最远,若粒子射入的速率为v1,轨迹如图甲所示, 甲 乙 设圆形磁场半径为R,由几何知识可知,粒子运动的轨道半径为r1=Rcos 60°=R;若粒子射入的速率为v2,轨迹如图乙所示,由几何知识可知,粒子运动的轨道半径为r2=Rcos 30°=R;根据Bqv=得r=,故v2∶v1=r2∶r1=∶1,故选项C正确. 4.(2018·全国卷Ⅰ·25)如图4,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E;在y<0的区域存在方向垂直于xOy平面向外的匀强磁场.一个氕核H和一个氘核H先后从y轴上y=h点以相同的动能射出,速度方向沿x轴正方向.已知H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场.H的质量为m,电荷量为q.不计重力.求: 图4 (1)H第一次进入磁场的位置到原点O的距离; (2)磁场的磁感应强度大小; (3)H第一次离开磁场的位置到原点O的距离. 【考点定位】 带电粒子在复合场中的运动、类平抛运动、圆周运动 【点评】 全国Ⅰ卷计算题中多年未考,这次还稍涉及原子核的知识,难度适中. 【难度】 中等 答案 (1)h (2) (3)(-1)h 解析 (1)H在电场中做类平抛运动,在磁场中做匀速圆周运动,运动轨迹如图所示. 设H在电场中的加速度大小为a1,初速度大小为v1,它在电场中的运动时间为t1,第一次进入磁场的位置到原点O的距离为s1,由运动学公式有s1=v1t1① h=a1t② 由题给条件,H进入磁场时速度的方向与x轴正方向夹角θ1=60°.H进入磁场时速度的竖直分量的大小为 a1t1=v1tan θ1③ 联立以上各式得s1=h④ (2)H在电场中运动时,由牛顿第二定律有 qE=ma1⑤ 设H进入磁场时速度的大小为v1′,由速度合成法则有 v1′=⑥ 设磁感应强度大小为B,H在磁场中运动的圆轨道半径为R1,由洛伦兹力公式和牛顿第二定律有 qv1′B=⑦ 由几何关系得s1=2R1sin θ1⑧ 联立以上各式得B=⑨ (3)设H在电场中沿x轴正方向射出的速度大小为v2,在电场中的加速度大小为a2,由题给条件得 (2m)v=mv⑩ 由牛顿第二定律有qE=2ma2⑪ 设H第一次射入磁场时的速度大小为v2′,速度的方向与x轴正方向夹角为θ2,入射点到原点的距离为s2,在电场中运动的时间为t2.由运动学公式有s2=v2t2⑫ h=a2t⑬ v2′=⑭ sin θ2=⑮ 联立以上各式得s2=s1,θ2=θ1,v2′=v1′⑯ 设H在磁场中做圆周运动的半径为R2,由⑦⑯式及粒子在匀强磁场中做圆周运动的半径公式得 R2==R1⑰ 所以出射点在原点左侧.设H进入磁场的入射点到第一次离开磁场的出射点的距离为s2′,由几何关系有 s2′=2R2sin θ2⑱ 联立④⑧⑯⑰⑱式得,H第一次离开磁场时的位置到原点O的距离为s2′-s2=(-1)h⑲ 5.(2018·全国卷Ⅲ·24)如图5,从离子源产生的甲、乙两种离子,由静止经加速电压U加速后在纸面内水平向右运动,自M点垂直于磁场边界射入匀强磁场,磁场方向垂直于纸面向里,磁场左边界竖直.已知甲种离子射入磁场的速度大小为v1,并在磁场边界的N点射出;乙种离子在MN的中点射出;MN长为l.不计重力影响和离子间的相互作用.求: 图5 (1)磁场的磁感应强度大小; (2)甲、乙两种离子的比荷之比. 【考点定位】 带电粒子在组合场中的运动、匀变速直线运动、圆周运动. 【难度】 中等 答案 (1) (2)1∶4 解析 (1)设甲种离子所带电荷量为q1、质量为m1,在磁场中做匀速圆周运动的半径为R1,磁场的磁感应强度大小为B,由动能定理有q1U=m1v① 由洛伦兹力公式和牛顿第二定律有 q1v1B=m1② 由几何关系知2R1=l③ 由①②③式得B=④ (2)设乙种离子所带电荷量为q2、质量为m2,射入磁场的速度为v2,在磁场中做匀速圆周运动的半径为R2.同理有q2U=m2v⑤ q2v2B=m2⑥ 由题给条件有2R2=⑦ 由①②③④⑤⑥⑦式得,甲、乙两种离子的比荷之比为 ∶=1∶4. 带电粒子在匀强磁场中的运动综合了洛伦兹力、牛顿运动定律、匀速圆周运动等知识,是高考命题的热点和重点,磁场叠加、安培力近年来也频繁考查,难度一般不大.,高考对于带电粒子在磁场中的运动的考查,近年多为选择题,难度适中,2018年在全国Ⅰ、Ⅱ、Ⅲ卷中出现在了计算题中,2017年全国Ⅲ卷也有复合场的计算题,但难度适中,所以复习时要重点复习,但不要过于繁、难. 考点1 磁场的基本性质与安培力 1.对磁场的理解 (1)磁感应强度是矢量,其方向与通电导线在磁场中所受力的方向垂直; (2)电流元必须垂直于磁场方向放置,公式B=才成立; (3)磁场中某点的磁感应强度是由磁场本身决定的,与通电导线受力的大小及方向都无关. 2.安培力大小的计算公式:F=BILsin θ(其中θ为B与I之间的夹角). (1)若磁场方向和电流方向垂直:F=BIL. (2)若磁场方向和电流方向平行:F=0. 3.安培力方向的判断:左手定则. 方向特点:垂直于磁感线和通电导线确定的平面. 4.两个常用的等效模型 (1)变曲为直:图6甲所示通电导线,在计算安培力的大小和判断方向时均可等效为ac直线电流. 图6 (2)化电为磁:环形电流可等效为小磁针,通电螺线管可等效为条形磁铁,如图乙. 5.求解磁场中导体棒运动趋势的方法 (1)分析:正确对导体棒进行受力分析,应特别注意通电导体棒受到的安培力的方向,安培力与导体棒和磁感应强度组成的平面垂直. (2)作图:必要时将立体的受力分析图转化为平面受力分析图,即画出与导体棒垂直的平面内的受力分析图. (3)求解:根据平衡条件或牛顿第二定律或动能定理列式求解. 命题热点1 磁场的叠加 (多选)(2018·河南省周口市期末)如图7甲所示,一长直导线沿南北方向水平放置,在导线下方有一静止的灵敏小磁针.现在导线中通以图甲所示的恒定电流,测得小磁针偏离南北方向的角度θ的正切值tan θ与小磁针离开导线的距离之间的关系如图乙所示.若该处地磁场的水平分量为B0,则下列判断中正确的是( ) 图7 A.通电后,小磁针的N极向纸里偏转 B.通电后,小磁针静止时N极所指的方向即为电流在小磁针处产生的磁场方向 C.电流在x0处产生的磁场的磁感应强度大小为B0 D.x0处合磁场的磁感应强度大小为2B0 答案 AC 解析 根据安培定则可知,通电后,小磁针的N极向纸里偏转,故A正确;磁场的磁感应强度是矢量,通电后,小磁针静止时N极所指的方向即为电流在小磁针处产生的磁场与地球的磁场的合磁场的方向,故B错误;电流在x0处产生的磁场的磁感应强度大小为B1,则tan θ=,所以B1=B0,故C正确;由矢量的合成可知,x0处合磁场的磁感应强度大小为B0,故D错误. 1.(多选)(2018·湖北省宜昌市调研)如图8所示,圆圈中的“×”表示电流方向垂直纸面向里,圆圈中的“·”表示电流方向垂直纸面向外.两根通电长直导线a、b平行水平放置,a、b 中的电流强度均为I,此时a受到的磁场力大小为F.当在a、b的上方再放置一根与a、b平行的通电长直导线c后,a受到的磁场力大小仍为F,图中abc正好构成一个等边三角形,则此时( ) 图8 A.b受到的磁场力大小为F B.b受到的磁场力大小为F C.c受到的磁场力大小为F D.c受到的磁场力大小为F 答案 BC 命题热点2 安培力作用下的平衡与运动 (2018·河北省“名校联盟”质量监测一)如图9所示,边长为l、质量为m的等边三角形导线框用绝缘细线悬挂于天花板,导线框中通一逆时针方向的电流,图中虚线过ab边中点和ac边中点,在虚线的下方有一垂直于导线框向里的匀强磁场,其磁感应强度大小为B,此时导线框处于静止状态,细线中的拉力为F1;保持其他条件不变,现将虚线下方的磁场移至虚线上方,此时细线中拉力为F2.导线框中的电流大小为( ) 图9 A. B. C. D. 答案 A 解析 当磁场在虚线下方时,通电导线的等效长度为l,受到的安培力方向竖直向上,故F1+BIl=mg,当磁场在虚线上方时,通电导线的等效长度为l,受到的安培力方向竖直向下,故F2=BIl+mg,联立可得I=,A正确. 2.(多选)(2017·全国卷Ⅱ·21)某同学自制的简易电动机示意图如图10所示.矩形线圈由一根漆包线绕制而成,漆包线的两端分别从线圈的一组对边的中间位置引出,并作为线圈的转轴.将线圈架在两个金属支架之间,线圈平面位于竖直面内,永磁铁置于线圈下方.为了使电池与两金属支架连接后线圈能连续转动起来,该同学应将( ) 图10 A.左、右转轴下侧的绝缘漆都刮掉 B.左、右转轴上下两侧的绝缘漆都刮掉 C.左转轴上侧的绝缘漆刮掉,右转轴下侧的绝缘漆刮掉 D.左转轴上下两侧的绝缘漆都刮掉,右转轴下侧的绝缘漆刮掉 答案 AD 解析 装置平面示意图如图所示. 如图所示的状态,磁感线方向向上,若形成通路,线圈下边导线中电流方向向左,受垂直纸面向里的安培力,同理, 上边导线中电流受安培力垂直纸面向外,使线圈转动.当线圈上边导线转到下边时,若仍通路,线圈上、下边中电流方向与图示方向相比均反向,受安培力反向,阻碍线圈转动.若要线圈连续转动,则要求左、右转轴只能上一侧或下一侧形成通路,另一侧断路.故选A、D. 考点2 带电粒子在有界磁场中的运动 1.基本公式:qvB=m,T= 重要结论:r=,T= 2.基本步骤:(1)画轨迹:依题意画出粒子运动轨迹,或可能的轨迹,找到临界情况的轨迹. (2)定圆心:入射点与出射点所受洛伦兹力方向的交点. (3)求半径或圆心角:由图中几何关系求半径从而可求出速度,求圆心角从而可求出时间. 3.基本“语言翻译”:运动语言→几何语言 速度→半径(m、q、B一定时r∝v) 时间→圆心角(t=T) 时间→弦长(圆心角θ<π时,圆心角越大,弧长越长,弦长越长,代表时间越长) 时间→弧长 4.圆的几个基本特点: (1)粒子从同一直线边界射入磁场和射出磁场时,入射角等于出射角.如图11,θ1=θ2=θ3. (2)粒子经过磁场时速度方向的偏转角等于其轨迹的圆心角(如图,α1=α2). 图11 (3)沿半径方向射入圆形磁场的粒子,出射时亦沿半径方向,如图12. 图12 图13 (4)磁场圆与轨迹圆半径相同时,以相同速率从同一点沿各个方向射入的粒子,出射速度方向相互平行.反之,以相互平行的相同速率射入时,会从同一点射出(即磁聚焦现象),如图13. (多选)(2018·山西省太原市二模)如图14,有理想边界的正方形匀强磁场区域abcd边长为L,磁场方向垂直纸面向里,磁感应强度大小为B.一群质量为m、带电荷量为+q的粒子(不计重力),在纸面内从b点沿各个方向以大小为的速率射入磁场,不考虑粒子间的相互作用,下列判断正确的是( ) 图14 A.从a点射出的粒子在磁场中运动的时间最短 B.从d点射出的粒子在磁场中运动的时间最长 C.从cd边射出的粒子与c的最小距离为(-1)L D.从cd边射出的粒子在磁场中运动的最短时间为 答案 ABD 解析 根据Bqv=m可得,r=2L,在磁场中运动的时间t=T,θ为轨迹对应的圆心角,由题中条件可知在磁场的轨迹为劣弧,所以弦长越长,圆心角越大,bd为最长的弦,所以从d 点射出的粒子在磁场中运动的时间最长,ba为最短的弦,从a点射出的粒子在磁场中运动的时间最短,故A、B正确;沿bc方向进入磁场的粒子在从cd边射出的粒子中与c点距离最近,在磁场中运动的时间最短,轨迹如图所示. 根据几何关系可求ec=(2-)L,所以C错误;轨迹圆心角为30°,所以运动时间t==,所以D正确. 3.(2018·山西省太原市三模)如图15,直角三角形abc内有方向垂直纸面向外的匀强磁场,磁感应强度的大小为B,∠a=30°,ac=2L,P为ac的中点.在P点有一粒子源可沿平行cb方向发出动能不同的同种正粒子,粒子的电荷量为q、质量为m,且粒子动能最大时,恰好垂直打在ab上.不考虑粒子重力及粒子间的相互作用力,下列判断正确的是( ) 图15 A.粒子动能的最大值为 B.ab上可能被粒子打中区域的长度为L C.粒子在磁场中运动的最长时间为 D.ac上可能被粒子打中区域的长度为L 答案 B 解析 动能最大,垂直打在d点,半径R1=L, 根据洛伦兹力提供向心力:qvB=m Ek=mv2=,A错误; 轨迹与ab相切时,打的位置最靠近a点: 由几何关系知(L-R2)sin 30°=R2, R2=, ae=(L-R2)cos 30°=×=L, ab上可能被粒子打中区域为de,长度为L,B正确; 粒子在磁场中运动半个圆周时,所用的时间最长:t==,C错误;ac上可能被粒子打中区域为Pf,区域的长度为,D错误. 4.(多选)(2018·福建省厦门大学附中第二次模拟)如图16所示,半径为R的圆形区域内有方向垂直于纸面向里的匀强磁场(图中未画出).两个质量、电荷量都相同的带负电的粒子,以相同的速率v从a点先后沿直径ac和弦ab的方向射入磁场区域,ab和ac的夹角为30°.已知沿ac方向射入的粒子在磁场中运动的时间为其圆周运动周期的,不计粒子重力.则( ) 图16 A.粒子在磁场中运动的轨道半径为R B.粒子在磁场中运动的轨道半径为2R C.沿ab方向射入的粒子在磁场中运动的时间为 D.沿ab方向射入的粒子在磁场中运动的时间为 答案 AD 解析 由于沿ac方向射入的粒子偏转90°,粒子从O点正下方的A点射出,如图轨迹1, 由几何关系知其运动半径为R,所以A正确,B错误; 沿ab方向入射的粒子其半径也为R,其轨迹只是将1顺时针旋转30°,其圆心为O′,由几何关系知四边形aOBO′为菱形,且∠aO′B=60°,所以沿ab方向入射的粒子在磁场中的运动时间为t=T=×=,所以C错误,D正确. 考点3 带电粒子在复合场中的运动 1.叠加场 明确粒子受几个力,结合运动情况,分析各力方向. (1)电场与磁场叠加:常见模型有速度选择器、磁流体发电机、电磁流量计、霍尔效应等. (2)电场、磁场、重力场叠加:无约束带电体在叠加场做直线运动时必为匀速直线运动;做圆周运动时必为匀速圆周运动,重力与电场力平衡,洛伦兹力提供向心力. 2.组合场 带电粒子依次经过各场,运动过程由各阶段不同性质的运动(圆周、类平抛、变速直线、匀速直线等)组合而成.(1)分别研究带电粒子在不同场区的运动. (2)分析与计算各阶段运动间的连接点的速度方向与大小是解题关键. (3)画出全过程运动示意图很重要. 3.交变场 带电粒子进入周期性变化的电场或磁场,其运动随之做周期性变化. (1)分析清楚复合场一个周期内的粒子运动过程,找到粒子运动时间、位移、速度等的周期性变化规律. (2)画出运动过程的示意图,有助于分析. 命题热点1 叠加场的应用实例 (多选)(2018·河北省衡水中学模拟)如图17所示,一对间距可变的平行金属板C、D水平放置,两板间有垂直于纸面向里的匀强磁场B.两板通过滑动变阻器与铅蓄电池相连,这种铅蓄电池能快速转换到“逆变”状态,即外界电压过低时能向外界提供一定的供电电压,当外界电压超过某一限定值时可转换为充电状态,闭合开关S后,有一束不计重力的带正电粒子从左侧以一定的速度v0射入两板间恰能做直线运动,现对入射粒子或对装置进行调整,则下列有关描述正确的是( ) 图17 A.若仅将带正电的粒子换成带负电的粒子,也能直线通过 B.若只增大两板间距到一定程度时可使铅蓄电池处于充电状态 C.若将滑动变阻器滑动触头P向a端滑动,可提高C板的电势 D.若只减小入射粒子的速度,可使铅蓄电池处于充电状态 答案 AB 解析 带正电的粒子恰好做直线运动,其电场力和洛伦兹力相平衡,由q=qv0B可知v0= ,若换成带负电的粒子,电场力和洛伦兹力都反向,仍平衡,能直线通过,故选项A正确;若增大两板间距到一定程度,电场力减小,正电粒子射入后受电场力和洛伦兹力作用堆积在极板上,将提高两板间电压,若此电压超过蓄电池的“逆变”电压就会使之处于“逆变”状态而被充电,故选项B正确;由于电容器C、D两板是彼此绝缘的,调节滑动触头P不起任何作用,故选项C错误;若减小入射粒子的速度,粒子所受洛伦兹力减小,有部分粒子会落在下极板上,将减小两板间电压,达不到“逆变”电压,故选项D错误. 5.(多选)(2018·广东省华南师大附中三模)利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图18所示是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,当元件中通入图示方向的电流I时,C、D两侧面会形成一定的电势差U.下列说法中正确的是( ) 图18 A.若C侧面电势高于D侧面,则元件中形成电流的载流子带负电 B.若C侧面电势高于D侧面,则元件中形成电流的载流子带正电 C.在地球南、北极上方测地磁场强弱时,元件工作面竖直放置时U最大 D.在地球赤道上方测地磁场强弱时,元件工作面竖直放置且与地球经线垂直时U最大 答案 AD 解析 若元件的载流子带负电,由左手定则可知,载流子受到的洛伦兹力方向向D侧面偏,则C侧面的电势高于D侧面的电势,故A正确;若元件的载流子带正电,由左手定则可知,载流子受到的洛伦兹力方向向D侧面偏,则D侧面的电势高于C侧面的电势,故B错误;在地球南、北极上方测地磁场强弱时,因磁场方向竖直,则元件的工作面水平放置时U最大,故C错误;地球赤道上方的地磁场方向水平,在地球赤道上方测地磁场强弱时,元件的工作面应保持竖直,当与地球经线垂直时U最大,故D正确. 命题热点2 带电粒子在组合场中的运动 (2018·山东省菏泽市上学期期末)如图19所示,在直角坐标系xOy 中的第一象限存在沿y轴负方向的匀强电场,在第二、三、四象限存在垂直纸面向外的匀强磁场.电场强度和磁感应强度都未知.第一象限中在坐标为(l,l)的P点由静止释放质量为m、带电荷量为q(q>0)的粒子(不计重力),该粒子第一次经过x轴时速度为v0,第二次经过x轴时的位置坐标为(-l,0),求: 图19 (1)电场强度E和磁感应强度B的大小; (2)粒子第三次经过x轴时的速度大小及方向. (3)粒子第四次经过x轴时的位置坐标. 答案 (1) (2)v0 方向与x轴正方向夹角为45° (3)(0,0) 解析 (1)粒子在P点静止释放,到达x轴过程中运用动能定理; Eql=mv 解得E= 粒子在匀强磁场中做匀速圆周运动,轨道半径设为r1,由洛伦兹力提供向心力: qBv0=m,解得r1= 粒子第二次经过x轴时的位置坐标为(-l,0), 故其轨道半径r1=l, 得B= (2)如图所示,粒子从y轴上的(0,l)处以平行x轴的速度v0进入电场,做匀变速曲线运动,加速度为a== 设经过时间t射出电场,水平位移为x,竖直位移为l, 则x=v0t,l=at2, 解得t=,x=2l 设水平分速度为vx,竖直分速度为vy, 则vx=v0,vy=at=v0 得粒子第三次经过x轴时的速度大小 v==v0,方向与x轴正方向夹角为45°. (3)由上面分析可知粒子第三次过x轴时坐标为(2l,0),再次进入磁场中做圆周运动的半径: r2==l 由几何关系得,粒子第四次过x轴时刚好过原点,即坐标为(0,0). 6.(2018·湖北省黄冈中学模拟)如图20甲所示,直角坐标系xOy中,第二象限内有沿x轴正方向的匀强电场,场强E=1 N/C,第一象限内有垂直坐标平面的交变磁场,磁场方向垂直纸面向外为正方向.在x轴上的点A(-2 m,0)处有一发射装置(没有画出)沿y轴正方向射出一个比荷=100 C/kg的带正电的粒子(可视为质点且不计重力),该粒子以v0 的速度进入第二象限,从y轴上的点C(0,4 m)进入第一象限.取粒子刚进入第一象限的时刻为t=0时刻,第一象限内磁场的磁感应强度按图乙所示规律变化.g=10 m/s2,求: 图20 (1)初速度v0大小; (2)粒子出磁场时的位置坐标; (3)粒子在磁场中运动的时间. 答案 (1)20 m/s (2)(9 m,0) (3) s 解析 (1)粒子在第二象限内做类平抛运动,设从A到C的时间为t,则|xA|=at2,yC=v0t,a= 联立解得v0=20 m/s (2)设粒子在C点的运动方向与y轴正方向的夹角为θ,在C点的速度为vC, 则tan θ=,得θ=30° cos θ=,得vC=40 m/s 粒子在第一象限的磁场中有:qvCB=m 解得r= m 粒子做圆周运动的周期T== s 故粒子在磁场中运动的轨迹如图所示, CE==8 m,则粒子在运动的第四个半圆的过程中从D点出磁场, OE=yC,DE=2rcos 30°,OD=OE-DE=9 m 粒子出磁场时的位置坐标为(9 m,0). (3)粒子在磁场中运动的时间t1=+= s. 1.(多选)(2018·广东省广州市4月模拟)如图1所示,在同一平面内有①、②、③三根等间距平行放置的长直导线,通入的电流强度分别为1 A、2 A、1 A,②的电流方向为c→d且受到安培力的合力方向水平向右,则( ) 图1 A.①的电流方向为a→b B.③的电流方向为e→f C.①受到安培力的合力方向水平向左 D.③受到安培力的合力方向水平向左 答案 BCD 解析 根据“同向电流相互吸引,异向电流相互排斥”,因②的电流方向为c→d且受到安培力的合力方向水平向右,可知①的电流方向为b→a,③的电流方向为e→f,选项A错误,B正确;①受到②③的排斥力,故安培力的合力方向水平向左,选项C正确;③受到② 的吸引力和①的排斥力,因②的吸引力大于①的排斥力,故③受到安培力的合力方向水平向左,选项D正确. 2.(2018·山西省晋城市二模)一正方形导体框abcd,其单位长度的电阻值为r,现将该正方形导体框置于如图2所示的匀强磁场中,磁感应强度的大小为B,用不计电阻的导线将导体框连接在电动势为E、不计内阻的电源两端,则关于导体框所受的安培力,下列描述正确的是( ) 图2 A.安培力的大小为,方向竖直向上 B.安培力的大小为,方向竖直向下 C.安培力的大小为,方向竖直向下 D.安培力的大小为,方向竖直向上 答案 B 解析 由题图可知,电路接通后流过导体框的电流方向为ad及abcd,假设导体框的边长为L,由欧姆定律可得ad边的电流大小为I1=,流过bc边的电流大小为I2=;又由左手定则可知ab、cd两边所受安培力大小相等、方向相反,ad、bc两边所受的安培力方向均竖直向下,则导体框所受的安培力大小为F=BI1L+BI2L=,故选项B正确. 3.(2018·福建省三明市上学期期末)如图3所示,质量为m、长为l的铜棒ab,用长度也为l的两根轻导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻导线静止在竖直方向,通入恒定电流后,棒向外偏转的最大角度为θ,重力加速度为g,则( ) 图3 A.棒中电流的方向为b→a B.棒中电流的大小为 C.棒中电流的大小为 D.若只增大轻导线的长度,则θ角变大 答案 C 解析 根据铜棒受到的安培力方向可知,电流的方向由a到b,故A错误;根据动能定理可知,BIl2sin θ-mgl(1-cos θ)=0-0,解得I=,故B错误,C正确;由I=可知,最大偏转角与导线的长度无关(公式中l为铜棒的长度),故D错误. 4.场强为E的匀强电场和磁感应强度为B的匀强磁场正交.如图4所示,质量为m的带电粒子在垂直于磁场方向的竖直平面内做半径为R的匀速圆周运动,设重力加速度为g,则下列结论不正确的是( ) 图4 A.粒子带负电,且q= B.粒子顺时针方向转动 C.粒子速度大小v= D.粒子的机械能守恒 答案 D 5.(多选)质量为m、带电荷量为q的小物块,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,磁感应强度为B,如图5所示,若带电小物块下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( ) 图5 A.小物块一定带正电荷 B.小物块在斜面上运动时做匀加速直线运动 C.小物块在斜面上运动时做加速度增大,而速度也增大的变加速直线运动 D.小物块在斜面下滑过程中,当小球对斜面压力为零时的速度为 答案 ABD 6.(多选)(2018·广东省惠州市模拟)如图6所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P以速度v垂直磁场正对着圆心O射入带正电的粒子,且粒子所带电荷量为q、质量为m,不考虑粒子重力,关于粒子的运动,以下说法正确的是( ) 图6 A.粒子在磁场中通过的弧长越长,时间也越长 B.出磁场的粒子其出射方向的反向延长线也一定过圆心O C.出磁场的粒子一定能垂直打在MN上 D.只要速度满足v=,入射的粒子出射后一定垂直打在MN上 答案 BD 解析 速度不同的同种带电粒子在磁场中做匀速圆周运动的周期相等,对着圆心入射的粒子,速度越大,在磁场中轨迹半径越大,弧长越长,轨迹对应的圆心角越小,由t=T知,运动时间t越小,故A错误;带电粒子的运动轨迹是圆弧,根据几何知识可知,对着圆心入射的粒子,其出射方向的反向延长线也一定过圆心,故B正确;速度不同,半径不同,轨迹对应的圆心角不同,对着圆心入射的粒子,出射后不一定垂直打在MN上,与粒子的速度大小有关,故C错误;速度满足v=时,粒子的轨迹半径为r==R,入射点、出射点、O点与轨迹的圆心构成正方形,入射的粒子出射后一定垂直打在MN上,故D正确. 7.(多选)(2018·广东省深圳市一调)如图7所示,竖直平行线MN、PQ间距离为a,其间存在垂直纸面向里的匀强磁场(含边界PQ),磁感应强度为B,MN上O处的粒子源能沿不同方向释放比荷为的带负电粒子,速度大小相等,方向均垂直磁场,粒子间的相互作用及重力不计,设粒子速度方向与射线OM夹角为θ,当粒子沿θ=60°入射时,恰好垂直PQ射出,则( ) 图7 A.从PQ边界射出的粒子在磁场中运动的最短时间为 B.沿θ=120°射入的粒子,在磁场中运动的时间最长 C.粒子的速率为 D.PQ边界上有粒子射出的长度为2a 答案 BD 8.(2018·河南省鹤壁市调研)如图8所示,一个He粒子从平行板电容器的左极板由静止释放后,经过一段时间恰好从右极板的小孔进入复合场且沿水平虚线ab向右运动到b点.不计粒子重力,下列说法正确的是( ) 图8 A.如果将He换成H,粒子在复合场中不能沿直线运动 B.如果将He换成H,粒子在复合场中不能沿直线运动 C.无论换成什么样的带电粒子,带电粒子都能沿直线运动 D.如果增大平行板电容器两板的电压,He粒子仍能沿直线运动 答案 B 解析 带电粒子在电场中加速时,根据动能定理得qU=mv2,可得v=,He粒子和H粒子的比荷相同,故两粒子进入复合场的速度相同,粒子进入复合场后,对粒子受力分析,满足qE=qvB,故粒子在复合场中沿直线运动,选项A错误;如果将He换成H,H粒子的速度大,故受到的洛伦兹力大,不能沿直线运动,选项B正确,C错误;增大平行板电容器两板的电压,粒子的速度增大,粒子受到的洛伦兹力增大,He粒子不能沿直线运动,选项D错误. 9.(2018·山西省长治、运城、大同、朔州、阳泉五地市联考)如图9所示的金属导体,长l、宽d、高h,导体中通有沿x正方向的恒定电流I,空间存在沿z轴负方向的匀强磁场,磁感应强度为B,已知金属导体中单位体积内自由电子个数为n,电子电荷量为e,则下列说法正确的是( ) 图9 A.金属导体的M面带正电 B.金属导体中电荷定向移动速率为 C.增加导体高度h,M、M′两面间的电压将增大 D.M、M′两面间的电势差为UMM′= 答案 B 解析 根据左手定则知,电子向上侧偏转,则M面带负电,故A错误;由电流的微观表达式I=neSv得金属导体中电荷定向移动速率为,故B正确;电子做定向移动,视为匀速运动,速度为v=,电子受电场力和洛伦兹力平衡,有e=evB得:U=Bhv=Bh=,即电压的大小和导体高度h无关,故C错误;由上式可知,由于M面带负电,所以M、M′两面间的电势差为UMM′=-,故D错误. 10.(2018·山东省烟台市上学期期末)如图10所示,在xOy坐标系中第一象限内存在垂直纸面向里的匀强磁场,第二象限内的部分区域存在匀强电场.一电荷量为+q、质量为m的带电粒子,从P(a,0)点沿与x轴成45°角的方向以初速度v0射入磁场中,通过y轴上的N(0,a)点进入第二象限后,依次通过一个非电场区域和一个匀强电场区域,到达x轴上某点时速度恰好为零.已知从粒子第一次通过N点到第二次通过N点所用时间为t0.求:(粒子重力不计) 图10 (1)磁场的磁感应强度大小; (2)带电粒子自P点开始到第一次通过N点所用的时间; (3)匀强电场的电场强度大小. 答案 (1) (2) (3) 解析 (1)带电粒子运动轨迹及电场方向如图所示 由几何关系可知R=a. 根据:qv0B=得:B= (2)由周期公式T==得时间t== (3)设粒子在非电场区域飞行时间为t1,位移为x1,在电场中飞行时间为t2,位移为x2, 则有t1+t2=,x1+x2=a 又x1=v0t1,x2=t2 解得x2=-a 从进入电场到减速为零,根据动能定理: -qEx2=0-mv 得E=. 11.(2018·河北省邯郸市第一次模拟)如图11所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,在边长为2L的正方形abcd区域(包括边界)内有方向垂直纸面向外的匀强磁场.一电子从y轴上的A(0,)点以大小为v0的速度沿x轴正方向射入电场,已知电子的质量为m、电荷量为e,正方形abcd的中心坐标为(3L,0),且ab边与x轴平行,匀强电场的电场强度大小E=. 图11 (1)求电子进入磁场时的位置坐标; (2)若要使电子在磁场中从ab边射出,求匀强磁场的磁感应强度大小B满足的条件. 答案 (1)(2L,0) (2)≤B< 解析 (1)电子在电场中做类平抛运动,轨迹如图所示:则有: 竖直方向有:y=at 加速度为:a= 水平方向为:t1= 竖直速度:vy=at1解得:y1=,vy=v0 所以电子射出电场时的速度方向与x轴成45°角,电子在电场中沿x轴正方向和沿y轴负方向运动的距离分别为L和,又因为A点的坐标是,电子在无电、磁场的区域内做匀速直线运动,则电子射入磁场区的位置坐标为(2L,0)且射入磁场区的速度大小v=v0,方向与x轴成45°角. (2)要使电子从ab边界射出,其运动轨迹的临界状态分别与ab和bc相切,当运动轨迹与ab相切时, 有r1+r1sin 45°=L 电子在磁场中运动,由洛伦兹力提供向心力, 有:evB1= 解得:B1= 当运动轨迹与bc相切时,有:r2+r2sin 45°=2L 电子在磁场中运动,由洛伦兹力提供向心力, 有:evB2=解得:B2= 匀强磁场的磁感应强度大小B满足的条件: ≤B<.查看更多