浙江省2020高考物理二轮复习专题一第四讲曲线运动讲义含解析

浙江省2020高考物理二轮复习专题一第四讲曲线运动讲义含解析

- 1 - 第四讲　曲线运动 知识内容 考试要求 备考指津 1.曲线运动 b 2.运动的合成与分解 c 3.平抛运动 d 4.圆周运动 d 5.向心加速度 d 6.向心力 d 7.生活中的圆周运动 c 1.平抛运动的规律及其研究方法， 圆周运动的角速度、线速度和向心 加速度是近几年命题的热点，且多 数与电场力、洛伦兹力联系起来考 查. 2.生活中的圆周运动命题范围很 大，需灵活运用. 　运动的合成与分解 【题组过关】 1．(2019·宁波检测)一轻杆两端分别固定质量为 mA 和 mB 的两个小球 A 和 B(可视为质 点)．将其放在一个光滑球形容器中从位置 1 开始下滑，如图所示，当轻杆到达位置 2 时球 A 与球形容器球心等高，其速度大小为 v1，已知此时轻杆与水平方向成 θ＝30°角，B 球的速 度大小为 v2，则(　　) A．v2＝ 1 2v1　　　　　　　　 B．v2＝2v1 C．v2＝v1 D．v2＝ 3v1 解析：选 C.球 A 与球形容器球心等高，速度 v1 方向竖直向下，速 度分解如图所示，有 v11＝v1sin 30°＝ 1 2v1，球 B 此时速度方向与杆 成 α＝60°角，因此 v21＝v2cos 60°＝ 1 2v2，沿杆方向两球速度相等， 即 v21＝v11，解得 v2＝v1，选项 C 正确． 2.如图所示，河的宽度为 L ，河水流速为 u ，甲、乙两船均以静水 中的速度 v 同时渡河．出发时两船相距 2L，甲、乙船头均与岸边成 60 °角，且乙船恰好能直达正对岸的 A 点．则下列判断正确的是(　　) A．甲船正好也在 A 点靠岸 B．甲船在 A 点下游靠岸 C．甲、乙两船到达对岸的时间相等 D．甲、乙两船可能在未到达对岸前相遇 - 2 - 解析：选 C.甲、乙两船在垂直河岸方向的分速度均为 vsin 60°，过河时间均为 t＝ L vsin 60°，故 C 正确．由乙恰好到达 A 点知，u＝vsin 30°＝ 1 2v，则甲沿河岸方向的速 度为 u＋ 1 2v＝v，沿河岸方向的位移为 v·t＝ L sin 60°<2L，故 A、B、D 错误． 3．(多选)如图所示，将质量为 2m 的重物悬挂在轻绳的一端，轻绳的另一端系一质量为 m 的小环，小环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为 d.现将小环从与定滑 轮等高的 A 处由静止释放，当小环沿直杆下滑距离也为 d 时(图中 B 处)，下列说法正确的是 (　　) A．小环刚释放时轻绳中的张力一定大于 2mg B．小环到达 B 处时，重物上升的高度也为 d C．小环在 B 处的速度与重物上升的速度大小之比等于 2 D．小环在 B 处的速度与重物上升的速度大小之比等于 2 2 解析：选 AC.由题意，释放时小环向下加速运动，则重物将加速上升，对重物由牛顿第二 定律可知绳中张力一定大于重力 2mg，所以 A 正确；小环到达 B 处时，重物上升的高度应为绳 子竖直部分缩短的长度，即Δh＝ 2d－d，所以 B 错误；根据题意，沿绳子方向的速度大小 相等，将小环在 B 处的速度沿绳子方向与垂直于绳子方向正交分解有 vBcos θ＝v 重，即 vB v重＝ 1 cos θ＝ 2，所以 C 正确，D 错误． 1．合运动性质和轨迹的判断方法：若加速度与初速度的方向在同一直线上，则为直线运 动，否则为曲线运动，加速度恒定则为匀变速，加速度不恒定则为非匀变速． 2．三种过河情景分析 (1)过河时间最短：船头正对河岸时，渡河时间最短，tmin＝ d v1(d 为河宽)． (2)过河路径最短(v2v1 时)：合速度不可能垂直于河岸，无法垂直渡河．最短航程 s 短＝ d cos α＝ v2 v1d. 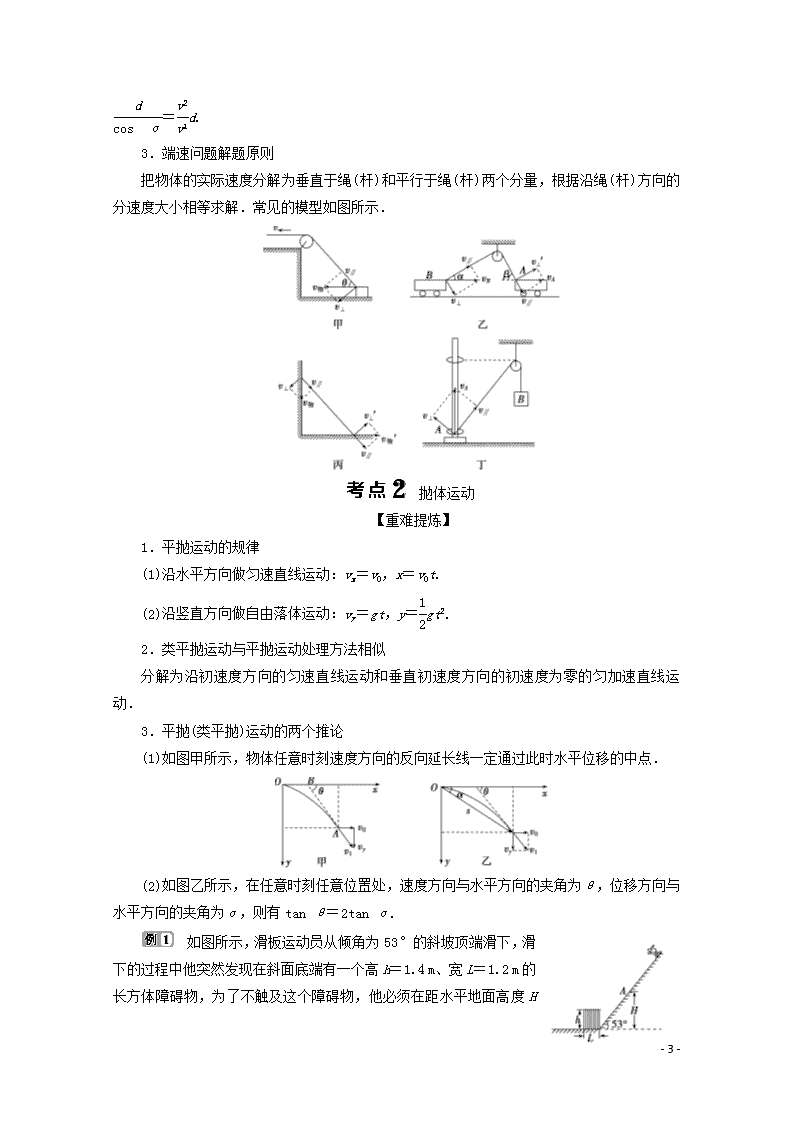- 3 - 3．端速问题解题原则 把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的 分速度大小相等求解．常见的模型如图所示． 　 　抛体运动 【重难提炼】 1．平抛运动的规律 (1)沿水平方向做匀速直线运动：vx＝v0，x＝v0t. (2)沿竖直方向做自由落体运动：vy＝gt，y＝ 1 2gt2. 2．类平抛运动与平抛运动处理方法相似 分解为沿初速度方向的匀速直线运动和垂直初速度方向的初速度为零的匀加速直线运 动． 3．平抛(类平抛)运动的两个推论 (1)如图甲所示，物体任意时刻速度方向的反向延长线一定通过此时水平位移的中点． (2)如图乙所示，在任意时刻任意位置处，速度方向与水平方向的夹角为θ，位移方向与 水平方向的夹角为α，则有 tan θ＝2tan α. 　如图所示，滑板运动员从倾角为 53°的斜坡顶端滑下，滑 下的过程中他突然发现在斜面底端有一个高 h＝1.4 m、宽 L＝1.2 m 的 长方体障碍物，为了不触及这个障碍物，他必须在距水平地面高度 H ＝3.2 m 的 A 点沿水平方向跳起离开斜面．已知运动员的滑板与斜面 间的动摩擦因数 μ＝0.1，忽略空气阻力，重力加速度 g 取 10 m/s2.(已 - 4 - 知 sin 53°＝0.8，cos 53°＝0.6)求： (1)运动员在斜面上滑行的加速度的大小； (2)若运动员不触及障碍物，他从 A 点起跳后落至水平面的过程所经历的时间； (3)运动员为了不触及障碍物，他从 A 点沿水平方向起跳的最小速度． [审题突破]　(1)题干中“不触及这个障碍物”说明：运动员在A 点起跳后下落高度 H－h 时的水平位移至少为________． (2)题干中“沿水平方向跳起离开斜面”说明：运动员在 A 点起跳后做________运动． [解析]　(1)设运动员连同滑板的质量为 m，运动员在斜面滑行的过程中，由牛顿第二定 律得 mgsin 53°－μmgcos 53°＝ma 解得 a＝gsin 53°－μgcos 53°＝7.4 m/s2. (2)运动员从斜面上起跳后沿竖直方向做自由落体运动，根据自由落体公式 H＝ 1 2gt2 解得：t＝ 2H g ＝0.8 s. (3)为了不触及障碍物，运动员以速度 v 沿水平方向起跳后竖直下落高度为 H－h 时，他 沿水平方向运动的距离为 H tan 53°＋L 设他在这段时间内运动的时间为 t′ 则：H－h＝ 1 2gt′2 H tan 53°＋L＝vt′ 解得 v＝6.0 m/s. [答案]　(1)7.4 m/s2　(2)0.8 s　(3)6.0 m/s 【题组过关】 考向一　平抛运动与斜面体的综合问题 1．如图所示，A、D 分别是斜面的顶端、底端，B、C 是斜面上的两个 点，AB＝BC＝CD，E 点在 D 点的正上方，与 A 等高．从 E 点以一定的水平速 度抛出质量相等的两个小球，球 1 落在 B 点，球 2 落在 C 点，关于球 1 和 球 2 从抛出到落在斜面上的运动过程(　　) A．球 1 和球 2 运动的时间之比为 2∶1 B．球 1 和球 2 动能增加量之比为 2∶1 C．球 1 和球 2 抛出时初速度之比为 2 2∶1 D．球 1 和球 2 运动时的加速度之比为 1∶2 - 5 - 解析：选 C. 因为 AC＝2AB，则 AC 的高度差是 AB 高度差的 2 倍，根据 h＝ 1 2gt2 得 t＝ 2h g ，解得运动的时间比为 1∶ 2，故 A 错误；根据动能定理得 mgh＝ΔEk，知球 1 和球 2 动 能增加量之比为 1∶2，故 B 错误；球 1 在水平方向上的位移是球 2 在水平方向上的位移的 2 倍，结合 x＝v0t，解得初速度之比为 2 2∶1，故 C 正确；平抛运动的加速度均为 g，两球的 加速度相同，故 D 错误． 2.如图所示，在斜面顶点以大小相同的速度 v0 同时水平向左与水 平向右抛出两个小球 A 和 B，两侧斜坡的倾角分别为 37°和 53°，小球 均落在坡面上，若不计空气阻力，则 A 和 B 两小球的运动时间之比为 (　　) A．16∶9　　　　　　　　　　 B．9∶16 C．3∶4 D．4∶3 解析：选 B.对于 A 球有 tan 37°＝ h x＝ gtA 2v0，解得 tA＝ 2v0tan 37° g ；同理对 B 有 tB＝ 2v0tan 53° g ，由此解得 tA tB＝ 9 16，故选项 B 正确，A、C、D 错误． 考向二　平抛运动中的临界问题 3．套圈游戏是一项很受欢迎的群众运动，要求每次从同一位置水平抛出圆环，套住与圆 环前端水平距离为 3 m 的 20 cm 高的竖直细杆，即为获胜．一身高 1.4 m 儿童从距地面 1 m 高 度，水平抛出圆环，圆环半径为 10 cm，要想套住细杆，他水平抛出的速度可能为(g＝10 m/s2)(　　) A．7.4 m/s B．9.0 m/s C．7.8 m/s D．8.2 m/s 解析：选 C.圆环做平抛运动，圆环距杆上端的竖直距离为 H＝0.8 m，又知圆环在竖直方 向做自由落体运动，则有 H＝ 1 2gt2，解得 t＝0.4 s，圆环后端与杆的水平距离为 3.2 m＝ v1·t，得 v1＝8 m/s，圆环前端与杆的水平距离为 3 m＝v2·t，得 v2＝7.5 m/s，所以要想套 住杆，圆环水平抛出的速度范围为 7.5 m/s＜v＜8 m/s，故选 C. 4．一带有乒乓球发射机的乒乓球台如图所示．水平台面的长和宽分别为 L1 和 L2，中间球 网高度为 h.发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓 球，发射点距台面高度为 3h.不计空气的作用，重力加速度大小为 g.若乒乓球的发射速率 v 在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则 v 的最大取值范 围是(　　) - 6 - A. L1 2 g 6h gR时，轨道对小 球的作用力方向向下，根据牛顿第二定律得，mg＋N＝m v2 R ，当 v 由 gR值逐渐增大时，轨道对 小球的弹力也逐渐增大，故 C 正确，B、D 错误． [答案]　C - 8 - 【题组过关】 考向一　水平面内的圆周运动 1．(2018·浙江选考 4 月)A、B 两艘快艇在湖面上做匀速圆周运动(如图)，在相同时间内， 它们通过的路程之比是 4∶3，运动方向改变的角度之比是 3∶2，则它们(　　) A．线速度大小之比为 4∶3 B．角速度大小之比为 3∶4 C．圆周运动的半径之比为 2∶1 D．向心加速度大小之比为 1∶2 解析：选 A.匀速圆周运动中线速度定义为单位时间内通过的圆弧长，即 v＝ l t，所以线速 度之比为 4∶3，A 正确；角速度定义为单位时间内转过的弧度角，即 ω＝ θ t ，且运动方向改 变角度等于圆心角，所以角速度之比为 3∶2，B 错误，半径 R＝ v ω，即半径之比为 8∶9，C 错 误，向心加速度 a＝vω，即向心加速度之比为 2∶1，D 错误． 2.(多选)如图所示，匀速转动的水平圆盘上放有质量分别为 2 kg 和 3 kg 的小物体 A、B，A、B 间用细线沿半径方向相连．它们到转轴的距离分别 为 rA＝0.2 m、rB＝0.3 m．A、B 与盘面间的最大静摩擦力均为重力的 0.4. g 取 10 m/s2，现极其缓慢地增大圆盘的角速度，则下列说法正确的是(　　) A．当 A 达到最大静摩擦力时，B 受到的摩擦力大小为 12 N B．当 A 恰好达到最大静摩擦力时，圆盘的角速度约为 4 rad/s　 C．当细线上开始有弹力时，圆盘的角速度为 2 30 3 rad/s D．在细线上有弹力后的某时刻剪断细线，A 将做向心运动，B 将做离心运动 解析：选 AC.增大圆盘的角速度，由于 B 的半径较大，B 先达到最大静摩擦力，所以 A 达 到最大静摩擦力时，B 受到的摩擦力大小为 FB＝kmBg＝12 N，选项 A 正确；设小物体 A 达到最 大静摩擦力时，圆盘的角速度为 ω1，此时细线的拉力为 T，则对 A：kmAg－T＝mAω21rA，对 B：T ＋kmBg＝mBω21rB，得 ω1＝10 2 13rad/s，选项 B 错误；设当细线上开始有弹力时，圆盘角速度 为 ω2，对 B：kmBg＝mBω22rB，解得 ω2＝ 2 30 3 rad/s，选项 C 正确；剪断细线，A 随圆盘做圆 - 9 - 周运动，B 将做离心运动，选项 D 错误． 考向二　竖直平面内的圆周运动 3.如图所示，质量为 m 的物体，沿着半径为 R 的半球形金属壳内 壁滑下，半球形金属壳竖直固定放置，开口向上，滑到最低点时速度大 小为 v，若物体与球壳之间的动摩擦因数为 μ，则物体在最低点时，下列说法不正确的是(　　) A．受到的向心力为 m v2 R B．受到的摩擦力为 μm v2 R C．受到的摩擦力为 μ(mg＋m v2 R ) D．受到的合力方向斜向左上方 解析：选 B.物体在最低点做圆周运动，则有 FN－mg＝m v2 R ，解得 FN＝mg＋m v2 R ，故物体受 到的滑动摩擦力 Ff＝μFN＝μ(mg＋m v2 R )，故 A、C 正确，B 错误．物体受到重力、水平向左的 摩擦力和竖直向上的支持力，故物体所受的合力斜向左上方，D 正确． 4.如图所示，过山车的轨道可视为竖直平面内半径为 R 的圆 轨道．质量为 m 的游客随过山车一起运动，当游客以速度 v 经过 圆轨道的最高点时(　　) A．处于超重状态 B．向心加速度方向竖直向下 C．速度 v 的大小一定为 gR D．座位对游客的作用力为 m v2 R 解析：选 B.游客做圆周运动，在最高点，受重力和轨道的压力，合外力提供向心力，合 外力向下，加速度竖直向下，游客处于失重状态，故 A 错误，B 正确；在最高点，根据向心力 公式得 mg＋N＝m v2 R ，只有当 N＝0 时，v＝ gR，故 C 错误；在最高点，根据向心力公式得 mg＋ N＝m v2 R ，解得 N＝m v2 R －mg，故 D 错误． 5．小球 P 和 Q 用不可伸长的轻绳悬挂在天花板上，P 球的质量大于 Q 球的质量，悬挂 P 球的绳比悬挂 Q 球的绳短．将两球拉起，使两绳均被水平拉直，如图所示．将两球由静止释 放．在各自轨迹的最低点，(　　) A．P 球的速度一定大于 Q 球的速度 B．P 球的动能一定小于 Q 球的动能 - 10 - C．P 球所受绳的拉力一定大于 Q 球所受绳的拉力 D．P 球的向心加速度一定小于 Q 球的向心加速度 解析：选 C.小球从释放到最低点的过程中，只有重力做功，由机械能守恒定律可知，mgL ＝ 1 2mv2，v＝ 2gL，绳长 L 越长，小球到最低点时的速度越大，A 项错误；由于 P 球的质量大 于 Q 球的质量，由 Ek＝ 1 2mv2 可知，不能确定两球动能的大小关系，B 项错误；在最低点，根据 牛顿第二定律可知，F－mg＝m v2 L ，求得 F＝3mg，由于 P 球的质量大于 Q 球的质量，因此 C 项 正确；由 a＝ v2 L ＝2g 可知，两球在最低点的向心加速度相等，D 项错误． 求解水平面、竖直面内圆周运动问题的思路 　 [课后作业(六)] (建议用时：40 分钟) 一、选择题 1.A、B 两艘快艇在湖面上做匀速圆周运动(如图)，在相同时间 内，它们通过的路程之比是4∶3，运动方向改变的角度之比是3∶2， 则它们(　　) A．线速度大小之比为 4∶3 B．角速度大小之比为 3∶4 C．圆周运动的半径之比为 2∶1 D．向心加速度大小之比为 1∶2 解析：选 A.因为相同时间内他们通过的路程之比是 4∶3，根据 v＝ s t，则 A、B 的线速度 之比为 4∶3，选项 A 正确；运动方向改变的角度之比为 3∶2，根据 ω＝ Δθ t ，则角速度之比 为 3∶2，选项 B 错误；根据 v＝rω 可得圆周运动的半径之比为 r1∶r2＝8∶9，选项 C 错误； 根据 a＝vω 得，向心加速度之比为 a1∶a2＝2∶1，选项 D 错误． - 11 - 2．(多选)(2019·湖州一模)如图所示，人在岸上拉船，已知船的质量为 m，水的阻力恒 为 f，当轻绳与水平面的夹角为 θ 时，船的速度为 v，此时人的拉力大小为 F，则(　　) A．人拉绳行走的速度为 vcos θ B．人拉绳行走的速度为 v cos θ C．船的加速度为 Fcos θ－f m D．船的加速度为 F－f m 解析：选 AC.人拉船时，绳对船的拉力的功率等于人拉绳的力的功率，F v 人＝F v 船 cos θ，所以人拉绳行走的速度 v 人＝v cos θ，选项 A 正确，B 错误；由于绳对船的拉力等于人拉 绳的力，即绳的拉力大小为 F，与水平方向成 θ 角，因此水平方向有 Fcos θ－f＝ma，得 a＝ Fcos θ－f m ，选项 C 正确，D 错误． 3.如图所示，光滑水平面上，小球 m 在拉力 F 作用下做匀速圆周运 动．若小球运动到 P 点时，拉力 F 发生变化，关于小球运动情况的说法正 确的是(　　) A．若拉力突然消失，小球将沿轨迹 Pa 做离心运动 B．若拉力突然变小，小球将沿轨迹 Pa 做离心运动 C．若拉力突然变大，小球将沿轨迹 Pb 做离心运动 D．若拉力突然变小，小球将沿轨迹 Pc 运动 答案：A 4．(多选)(2019·舟山模拟)如图所示，一固定斜面倾角为 θ， 将小球 A 从斜面顶端以速率 v0 水平向右抛出，击中了斜面上的 P 点； 将小球 B 从空中某点以相同速率 v0 水平向左抛出，恰好垂直斜面击中 Q 点．不计空气阻力，重力加速度为 g，下列说法正确的是(　　) A．若小球 A 在击中 P 点时速度方向与水平方向所夹锐角为φ，则 tan θ＝2tan φ B．若小球 A 在击中 P 点时速度方向与水平方向所夹锐角为 φ，则 tan φ＝2tan θ C．小球 A、B 在空中运动的时间比为 2tan 2θ∶1 D．小球 A、B 在空中运动的时间比为 tan 2θ∶1 解析：选 BC.由题图可知，斜面的倾角 θ 等于小球 A 落在斜面上时的位移与水平方向的 - 12 - 夹角，由 tan φ＝ gt v0，tan θ＝ 1 2gt2 v0t 可知：tan φ＝2tan θ，选项 A 错误，B 正确；设小球 A 在空中运动的时间为 t1，小球 B 在空中运动的时间为 t2，则由平抛运动的规律可得：tan θ＝ 1 2gt v0t1，tan θ＝ v0 gt2，则 t1 t2＝ 2tan 2θ 1 ，选项 C 正确，D 错误． 5．质量为 2 kg 的质点在 xOy 平面上做曲线运动，在 x 方向的速度图象和 y 方向的位移图 象如图所示，下列说法不正确的是(　　) A．质点的初速度为 5 m/s B．质点所受的合外力为 3 N，做匀加速曲线运动 C．2 s 末质点速度大小为 6 m/s D．2 s 内质点的位移大小约为 12 m 解析：选 C.由 x 方向的速度图象可知，在 x 方向的加速度为 1.5 m/s2，受力 Fx＝3 N，由 y 方向的位移图象可知在 y 方向做匀速直线运动，速度为 vy＝4 m/s，受力 Fy＝0.因此质点的 初速度为 5 m/s，A 选项正确；受到的合外力为 3 N，显然，质点初速度方向与合外力方向不在 同一条直线上，B 选项正确；2s 末质点速度应该为 v＝ 62＋42m/s＝2 13m/s，C 选项错误； 2 s 内水平方向上位移大小 x＝vxt＋ 1 2at2＝9 m，竖直方向上位移大小 y＝8 m，合位移大小 l＝ x2＋y2＝ 145 m≈12 m，D 选项正确． 6.如图所示，当汽车静止时，车内乘客看到窗外雨滴沿竖直方向 OE 匀速运动．现从 t＝0 时汽车由静止开始做甲、乙两种匀加速启动，甲启 动后 t1 时刻，乘客看到雨滴从 B 处离开车窗，乙启动后 t2 时刻，乘客 看到雨滴从 F 处离开车窗，F 为 AB 中点，则 t1∶t2 为(　　) A．2∶1　　　　　　　　　　 B．1∶ 2 C．1∶ 3 D．1∶( 2－1) 解析：选 A.由题意可知，在乘客看来，雨滴在竖直方向上做匀速直线运动，在水平方向 做匀加速直线运动，因分运动与合运动具有等时性，则 t1∶t2＝ AB v ∶ AF v ＝2∶1. 7.有 A、B 两小球，B 的质量为 A 的两倍．现将它们以相同速率沿 同一方向抛出，不计空气阻力．图中①为 A 的运动轨迹，则 B 的运动 轨迹是(　　) - 13 - A．① B．② C．③ D．④ 解析：选 A.由于不计空气阻力，因此小球以相同的速率沿相同的方向抛出，在竖直方向 做竖直上抛运动，水平方向做匀速直线运动，竖直方向的初速度相同，加速度为重力加速度， 水平方向的初速度相同，因此两小球的运动情况相同，即 B 球的运动轨迹与 A 球的一样，A 项 正确． 8.距地面高 5 m 的水平直轨道上 A、B 两点相距 2 m，在 B 点用细线 悬挂一小球，离地高度为 h，如图．小车始终以 4 m/s 的速度沿轨道匀 速运动，经过 A 点时将随车携带的小球由轨道高度自由卸下，小车运动 至 B 点时细线被轧断，最后两球同时落地．不计空气阻力，取重力加 速度的大小 g＝10 m/s2.可求得 h 等于(　　) A．1.25 m B．2.25 m C．3.75 m D．4.75 m 解析：选 A.根据两球同时落地可得 2H g ＝ dAB v ＋ 2h g ，代入数据得 h＝1.25 m，选项 A 正 确． 9.如图所示，在同一竖直平面内，小球 a、b 从高度不同的两点 (ha>hb)分别以初速度 va 和 vb 沿水平方向抛出，经时间 ta 和 tb 后落到 与两抛出点水平距离相等的 P 点，若不计空气阻力，则(　　) A．ta＞tb，va＜vb B．ta＞tb，va＞vb C．ta＜tb，va＜vb D．ta＜tb，va＞vb 解析：选 A.由平抛运动规律可知：h＝ 1 2gt2，x＝v0t，根据题中条件，因为 ha＞hb，所以 ta ＞tb，又因为 xa＝xb，故 va＜vb，所以 A 选项正确． 10.如图所示，做匀速直线运动的小车 A 通过一根绕过定滑轮的 长绳吊起一重物 B，设重物和小车速度的大小分别为 vB、vA，则(　　) A．vA＞vB B．vA＜vB C．绳的拉力等于 B 的重力 D．绳的拉力小于 B 的重力 解析：选 A.小车 A 向左运动的过程中，小车的速度是合速度，可 分解为沿绳方向与垂直于绳方向的速度，如图所示，由图可知 vB ＝ vAcosθ，则 vB＜vA，小车向左运动的过程中 θ 角减小，vB 增大，B 向上 做加速运动，故绳的拉力大于 B 的重力． 二、非选择题 - 14 - 11．一物体在光滑水平面上运动，它在 x 轴方向和 y 轴方向上的两个分运动的速度—时 间图象如图所示． (1)判断物体的运动性质； (2)计算物体的初速度大小； (3)计算物体在前 3 s 内和前 6 s 内的位移大小． 解析：(1)由题图可知，物体在 x 轴方向做匀速直线运动，在 y 轴方向做匀变速运动，先 减速再反向加速，所以物体做匀变速曲线运动． (2)vx0＝30 m/s，vy0＝－40 m/s v0＝ v＋v＝50 m/s. (3)x3＝vxt＝90 m |y3|＝|vy0 2 |t＝60 m 则 l1＝ x＋y＝30 13 m. x6＝vxt′＝180 m y6＝vyt′＝ 40－40 2 ×6 m＝0 则 l2＝x6＝180 m. 答案：(1)匀变速曲线运动　(2)50 m/s (3)30 13 m　180 m 12.如图所示，半径为 r1＝1.8 m 的 1 4光滑圆弧轨道末端水平， 固定在水平地面上，与竖直截面为半圆形的坑平滑连接，bd 为坑 沿水平方向的直径．现将质量为 m＝1.0 kg 的小球从圆弧顶端a 点 由静止释放，小球离开 b 点后击中坑壁上的 c 点．测得 c 点与水 平地面的竖直距离为 h＝1.8 m，重力加速度 g 取 10 m/s2.求： (1)小球刚到达轨道末端 b 点时对轨道的压力 FN； (2)半圆形坑的半径 r2. 解析：(1)小球沿光滑轨道滑下． 由机械能守恒定律得 mgr1＝ 1 2mv2 - 15 - 到达 b 点时，支持力与重力的合力提供向心力 F 支－mg＝ mv2 r1 根据牛顿第三定律，FN＝F 支 联立解得 FN＝3mg＝30 N. (2)小球从 b 点做平抛运动， 竖直方向上 h＝ 1 2gt2 水平方向上 x＝vt 故小球从 b 到 c 过程的水平位移 x＝v 2h g ＝3.6 m 由几何关系得，r22＝(x－r2)2＋h2 解得 r2＝2.25 m. 答案：(1)30 N　(2)2.25 m