高中物理竞赛模拟试题1及解析

高中物理竞赛模拟试题1及解析

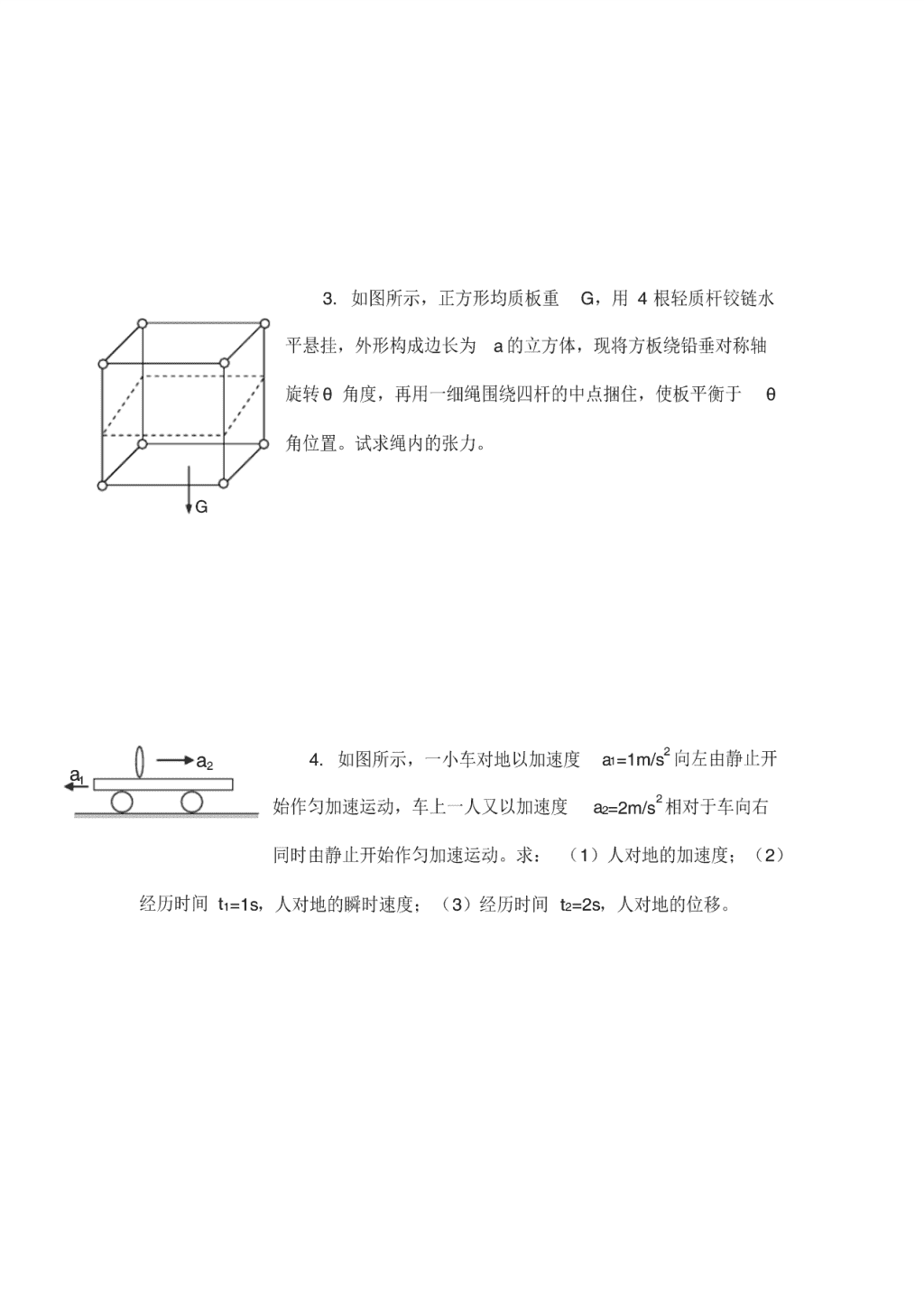
物理竞赛复赛模拟卷 1. 光子火箭从地球起程时初始静止质量 （包括燃料） 为 M 0，向相距为 R=1.8 ×1061.y.（光年）的远方仙女座星飞行。要求火箭在 25 年（火箭时间）后到达 目的地。引力影响不计。 1）、忽略火箭加速和减速所需时间， 试问火箭的速度应为多大？ 2）、设到达 目的地时火箭静止质量为 M 0ˊ，试问 M 0/ M 0ˊ的最小值是多少？ 2. 如图所示，地面上的观察者认为在地面上同时 发生的两个事件 A 和 B，在相对地面以速度 u （ u 平 行于 x 轴，且与正方向同向）运动的火箭上的观察者 的判断正确的是（ ） A、A 早于 B B、B 早于 A C、A、B 同时发生 D、无法判断 x y z O u A B 3. 如图所示，正方形均质板重 G，用 4 根轻质杆铰链水 平悬挂，外形构成边长为 a 的立方体，现将方板绕铅垂对称轴 旋转 θ角度，再用一细绳围绕四杆的中点捆住，使板平衡于 θ 角位置。试求绳内的张力。 4. 如图所示，一小车对地以加速度 a1=1m/s2 向左由静止开 始作匀加速运动，车上一人又以加速度 a2=2m/s2 相对于车向右 同时由静止开始作匀加速运动。求： （1）人对地的加速度； （2） 经历时间 t1=1s，人对地的瞬时速度； （3）经历时间 t2=2s，人对地的位移。 G 1a 2a 5．有一小直径为 d 的试管，管内装有理想气体，其中有一段质量 m=2g 的 水银将理想气体和空气隔开。 当试管口向上时， 气体在试管中的长为 L 1（图 24-30 （a）中的（ a）），当将管口向下时，气体在试管中长为 L 2（图 24-30（b）中的 （b）），试求 L 2/L 1 为多少？ 6．有一个两端开口、 粗细均匀的 U 型玻璃细管， 放置在竖直平 面内，处在压强为 0p 的大气中，两个竖直支管的高度均为 h，水平 管的长度为 2h，玻璃细管的半径为 r,r?h，今将水平管内灌满密度为 ρ的水银，如图所示。 1．如将 U 型管两个竖直支管的开口分别封闭起来，使其管内空气压强均等 于大气压强，问当 U 型管向右作匀加速移动时，加速度应多大才能使水平管内 水银柱长度稳定为 h 3 5 。 2．如将其中一个竖直支管的开口封闭起来，使其管内气体压强为 1atm，问 当 U 型管绕以另一个竖直支管（开口的）为轴作匀速转动时，转数 n 应为多大 才能使水平管内水银柱长度稳定为 h 3 5 。 （U 型管作以上运动时，均不考虑管内水银液面的 h h2 A h 3 1 B a 倾斜） 7. 有一块透明光学材料，由折射率略有不同的许多相互平行 的，厚度 d=0.1mm 的薄层紧密连接构成，图 33-40 表示各薄层互 相垂直的一个截面， 若最下面一层的折射率为 n0，从它往上数第 K 层的折射率为 nK=n0-K v，其中 n0=1.4,v=0.025，今有一光线以入射 角 i=60°射向 O 点，求此光线在这块材料内能达到的最大深度？ 8. （1）所示为一凹球面镜，球心为 C，内盛透明液体，已知 C 至液面高度 CE 为 40.0cm，主轴 CO 上有一物 A，物离液面高度 AE 恰好为 30.0cm 时，物 A 的实像和物处于同一高度。 实验时光圈直径很小， 可以保证近轴光线成像。 试求该透明液体的折射率 n。 （2）体温计横截面如图所示，已知细水银柱 A 离圆柱面 顶点 O 的距离为 2R，R 为该圆柱面半径， C 为圆柱 r i O 0 1 2 1n 0n 2n 4n 3n 5n R2 OC E R 面中心轴位置。玻璃的折射率 n=3/2，E 代表人眼，求图示横截面上人眼所 见水银柱像的位置、虚实、正倒和放大倍数。 9．如图所示，两个固定的均匀带电球面 A 和 B 分别带电 4Q 和 Q（Q>0）。 两球心之间的距离 d 远大于两球的半径，两球心的连线 MN 与两球面的相交处 都开有足够小的孔， 因小孔而损失的电量可以忽略不计。 一带负电的质点静止地 放置在 A 球左侧某处 P 点，且在 MN 直线上。设质点从 P 点释放后刚好能穿越 三个小孔，并通过 B 球的球心。试求质点开始时所在的 P 点与 A 球球心的距离 x 应为多少？ 10．如图所示，在真空中有 4 个半径为 a 的不带电的相同导体球，球心分别 位于边长为 r（r?a）的正方形的 四个顶点上。首先，让球 1 带电 荷 Q（Q?0），然后取一细金属丝， 其一端固定于球 1 上，另一端分 别依次与球 2、3、4、大地接触， 每次接触时间都足以使它们达到 静电平衡。 设分布在细金属丝上的电荷可忽略不计。 试求流入大地的电量的表达 式。 x d M N A B QQ4 P 1. 光子火箭从地球起程时初始静止质量 （包括燃料） 为 M 0，向相距为 R=1.8 ×1061.y.（光年）的远方仙女座星飞行。要求火箭在 25 年（火箭时间）后到达 目的地。引力影响不计。 1）、忽略火箭加速和减速所需时间， 试问火箭的速度应为多大？ 2）、设到达 目的地时火箭静止质量为 M 0ˊ，试问 M 0/ M 0ˊ的最小值是多少？ 分析： 光子火箭是一种设想的飞行器，它利用“燃料”物质向后辐射定向光 束，使火箭获得向前的动量。求解第 1 问，可先将火箭时间 a250 （年）变换 成地球时间 ，然后由距离 R 求出所需的火箭速度。 火箭到达目的地时， 比值 0 0 M M 是不定的，所谓最小比值是指火箭刚好能到达目的地，亦即火箭的终速度为零， 所需“燃料”量最少。利用上题（本章题 11）的结果即可求解第 2 问。 解： 1）火箭加速和减速所需时间可略，故火箭以恒定速度 飞越全程，走 完全程所需火箭时间（本征时间）为 a250 （年）。利用时间膨胀公式，相应 的地球时间为 2 2 0 1 c 因 R 故 2 2 0 1 c R 解出 10 2 2 0 2 2 2 0 2 1096.011 1 c R cc R c c 可见，火箭几乎应以光速飞行。 （2）、火箭从静止开始加速至上述速度 ，火箭的静止质量从 M 0 变为 M ， 然后作匀速运动，火箭质量不变。最后火箭作减速运动，比值 0 0 M M 最小时，到达 目的地时的终速刚好为零，火箭质量从 M 变为最终质量 0M 。加速阶段的质量 变化可应用上题（本章题 11）的（ 3）式求出。因光子火箭喷射的是光子，以光 速 c 离开火箭，即 u=c，于是有 2 1 0 1 1 M M （1） c 为加速阶段的终速度，也是减速阶段性的初速度。对减速阶段，可 应用上题（本章题 11）的（ 4）式，式中的 m0 以减速阶段的初质量 M 代入。又 因减速时必须向前辐射光子，故 u=-c，即有 2 1 0 1 1 M M （2） 由（ 1）、（2）式，得 10 2 0 2 2 2 0 2 2 0 104414 1 1 c R c R M M 2. 如图 52-1 所示，地面上的观察者认为在地面上同时发生的两个事件 A 和 B，在相对地面以速度 u （ u 平行于 x 轴，且与正方 向同向）运动的火箭上的观察者的判断正确的是 （ ） A、A 早于 B B、B 早于 A C、A、B 同时发生 D、无法判断 解：在地面（ S 系）上， ,AB xxx 0AB ttt ，在火箭（ S 系）中， 22 c uxtr c uxtrttt A A B BAB BA A AB xx c uxttr 2 BA A xx c ux 2 因 0r ， 0u ， 0BA xx ，故 0t 。即从火箭上观察， B 事件在前， A 事件在后，选 B。 3. 如图 11-195 所示，正方形均质板重 G，用 4 根轻质杆 铰链水平悬挂，外形构成边长为 a 的立方体，现将方板绕铅垂 对称轴旋转 θ角度，再用一细绳围绕四杆的中点捆住，使板平 衡于 θ角位置。试求绳内的张力。 分析： 初看此题，一般都会觉的比较复杂，因为题中铰链 就有 8 个，加上 4 根轻质杆与绳子有 4 个接触点，一共有 12 个受力点， 而且初看甚至想象不出木板旋转 θ角度以后整个系统是什么样子， 即 x y z O u A B 图 52-1 G 图 11-195 使把各个受力点的力逐个画出来也无济于事。应该先想一想哪些点都是对称的 （等价的） ，找出最基本的部分，再把空间方向确定下来，然后好画出各个力点 的受力情况。 解：把木板绕铅垂对称轴旋转 θ角度以后， 系统虽然不是一个很对称的立方 体，但把系统绕铅直轴旋转 90 度的整数倍，系统的与自身重合，说明四根轻杆 的受力情况是完全一样的。系统处于平衡状态，把四根轻杆，木板，绳组成的部 分看成刚体， 则刚体受四个铰接部分的力而平衡， 重力方向的平衡可以得出， 竖 直方向对每根轻杆的拉力 T 上 为： GT上4 （1） 而铰接处是否对轻杆有水平方向的作用力， 暂时还不好确定， 不过可以为 N// ，从俯图来看四根轻杆的受力情况（如图 11-196 所示） ： 图中虚线表示正方形对角线的外延部分，如果 N// 不在对角线 方向上，则四个 N// 对 O 点有一个力偶矩，将使得下面的部分旋转，与平衡假设 相矛盾，因此水平弹力必然在对角线方向，要么都向外，要么都向里（设向外为 正，这种设法不会影响结果） 。 同样的道理，把木板隔离开来，可知木板对轻杆往下的拉力 下T 为： GT下4 （2） 而水平方向的作用力必沿对角线方向（否则木板 旋转），木板对杆的作用力向里向外的性质与上端铰链 的方向相同，否则以绳对杆的作用点为支点，力矩无 O //N 图 11-196 x y //N//T //T //N O 图 11-197 法平衡。 下面再看整个系统的俯视图（如图 11-197 所示） ，把轻杆隔离出来作为平衡 的刚性杆，利用力的平衡条件和力矩的平衡条件可求出拉力 T 的大小。 绳作用在每根转杆的中点， 在俯视图上不难看出， 绳子构成一个正方形， 且 在水平面内， 因而可以知道绳对轻杆仅有水平面内， 因而可以知道绳对轻杆仅有 水平面内的拉力，轻杆在竖直方向上力的平衡是满足的： 下上 TT （3） 取一根轻杆为研究对象不难求出 //N 与 //N 的关系， 以及 //N 与 //T 的关系， 设 绳的张力为 T，则水平合力 TT 2// 。 x 方向水平力平衡： 2 si n 2 s i n //// NN （4） y 方向水平力平衡： TTNN 2 2 c o s 2 c o s ////// （5） 在过轻杆的竖直面内来分析力矩平衡（只研究平面内转矩） ，如图 11-198。 对于 A 点，力矩平衡 2 si n2c o s 2 si n// aTaN 下 （6） 联合（ 2）、（4）、（5）、（6）式可得 c o s2 2 c o sG T //T A B 下T 2min// N 2 min// N 2 sin2a cosa 上T 图 11-198 4. 如图 12-30 所示，一小车对地以加速度 a1=1m/s2 向左由 静止开始作匀加速运动，车上一人又以加速度 a2=2m/s2 相对于 车向右同时由静止开始作匀加速运动。求： （1）人对地的加速 度；（2）经历时间 t1=1s，人对地的瞬时速度； （3）经历时间 t2=2s，人对地的位 移。 解：（1） 车地人车人地 aaa a1 与 a2 方向相反选 a2 为正方向 则 22/2 smsma人地 2/1 sm （2）t=1s 时， 2 /m s人车 sm/1车地 smsm /1/2人地 sm/1 （3） 2/1 sma人地 msta 221 2 1 2 1 22 5．有一小直径为 d 的试管，管内装有理想气体，其中有一段质量 m=2g 的 水银将理想气体和空气隔开。 当试管口向上时， 气体在试管中的长为 L 1（图 24-30 （a）中的（ a）），当将管口向下时，气体在试管中长为 L 2（图 24-30（b）中的 （b）），试求 L 2/L 1 为多少？ 解： 如果是等温过程，可得理想气体的状态方程 1a 2a 图 12-30 常数PV 对于上述两种情况，可有 2211 VPVP 现在考虑在每一情况作用中在气体上的压强， 如图 24-30 （b）所示，可得 S WP S WP P P V V 大气 大气 2 1 1 2 式中 S 为试管内部的截面积， W 为水银的重量， W=mg，则 S mgP S mgP SL SL V V 大气 大气 1 2 1 2 消去 S 得 2 2 1 2 4 4 d mgP d mgP L L 大气 大气 6．有一个两端开口、粗细均匀的 U 型玻璃细管，放置在竖直平面内，处 在压强为 0p 的大气中，两个竖直支管的高度均为 h，水平管的长度为 2h，玻璃 细管的半径为 r,r?h，今将水平管内灌满密度为 ρ的水银， 如图 24-54（a）所示。 1．如将 U 型管两个竖直支管的开口分别封闭起来，使其管内空气压强均等 于大气压强，问当 U 型管向右作匀加速移动时，加速度应多大才能使水平管内 水银柱长度稳定为 h 3 5 。 2．如将其中一个竖直支管的开口封闭起来，使其管内气体压强为 1atm，问 1LP atP 2L atP P 图 24-30（b） h h2 图 24-54（a） 当 U 型管绕以另一个竖直支管（开口的）为轴作匀速转动时，转数 n 应为多大 才能使水平管内水银柱长度稳定为 h 3 5 。 （U 型管作以上运动时，均不考虑管内水银液面的倾斜） 解： 1、当 U 型管向右加速移动时，水平管内的水银柱将向左边的竖直 支管中移动， 其稳定的位置是留在水平管内的水银柱所受的水平方向的合力 等于使其以恒定加速度 a 向右运动时所需的力。 由于竖直支管内空气在膨胀或压 缩前后的温度相等，根据气态方程有 右管： hSphSp 10 3 4 左管： hSphSp 20 3 2 S 为管的截面积，图 24-54（b）中， A、B 两处压强分别为： ghpp A 3 1 2 1ppB 而留在水平管内的水银柱质量 hSm 3 5 其运动方程为 amSpp BA )( 由以上各式可得 )20/()49( 0 hghpa A h 3 1 B a 图 24-54（b） 2．当 U 型管以开口的竖直支管为轴转动时，水平管内的水银柱将向封闭 的竖直支管中移动，其稳定位置是水平管内的水银柱所受的水平方向的合力， 正好等于这段水银柱作匀速圆周运动所需的向心力。 由于封闭竖直支管内空气 在压缩前后的温度相等，根据气态方程有 hShSp 3 2 0 S 为管的截面积。图 24-54（c）中 A、B 两处的压强分别为 ghpp A 3 1 0ppB 留在水平管内的水银柱的质量 hSm 3 5 其运动方程为 mRnRmSpp BA 222 4)( 其中 hR 6 7 由以上各式可得 2 1 22 0 )140/()69( hghpn 7. 有一块透明光学材料，由折射率略有不同的许多相互平行 的，厚度 d=0.1mm 的薄层紧密连接构成，图 33-40 表示各薄层互 相垂直的一个截面， 若最下面一层的折射率为 n0，从它往上数第 K B A 3/h 图 24-54（c） r i O 0 1 2 1n 0n 2n 4n 3n 5n 图 33-40 层的折射率为 nK =n0-K v，其中 n0=1.4,v=0.025，今有一光线以入射角 i=60°射向 O 点，求此光线在这块材料内能达到的最大深度？ 解：设光线进入材料后的折射角为 r，则根据折射定律有 rni sinsin 0 ，此 光线从最下面一层进入向上数第一层时，入射角为 02 r ，折射角为 12 r ， 同样根据折射定律有 1100 2 sin 2 sin nn ， 也即 1100 c o sc o s nn 光线从第一层进入第二层时，同样可得 1201 c o sc o s nn 综合以上分析可得： KKnnnn c o sc o sc o sc o s 221100 因为 0025.00 KnnK ，所以 Kcos 随着 K 的增大而增大， K 则随着 K 的增大而减小， 即光线在顺序变化的介质中传播时将偏向折射率变大的方向。 满 足上式又当 Kcos 最接近 1 的 K 值即为光线能进入的最深薄层的序号， 光线在这 个薄层上将发生全反射，然后又逐层返回下面最后射出透明材料。 因此求出能满足下式的 K 的最大值 1c o sc o sc o s 0 0000 Kn n n n K K 因为 irnn sinsincos 000 代入上式得： 1si nc o s 0 Kn i K 解得： 76.21 025.0 866.041.1sin0 inK 取小于 21.76 的最大整数， 得 K=21，即在 n0 上面第 21 层下表面就是光线能 到达的最深处，所以光线在这块透明材料内能达到的最大深度是 .2.21.0221 mmmmdKh 8. （1）图 33-98 所示为一凹球面镜，球心为 C，内盛透明液体，已知 C 至液面 高度 CE 为 40.0cm，主轴 CO 上有一物 A，物离液面高度 AE 恰好为 30.0cm 时，物 A 的实像和物处于同一高度。实验时光圈直径很小，可以保证近轴 光线成像。试求该透明液体的折射率 n。 （2）体温计横截面如图 33-99 所示， 已知细水银柱 A 离圆柱 面顶点 O 的距离为 2R，R 为该圆柱面半径， C 为圆柱面 中心轴位置。玻璃的折射率 n=3/2，E 代表人眼，求图示 横截面上人眼所见水银柱像的位置、虚实、正倒和放大倍数。 分析： （1）通过折射定律和光圈足够小的条件可求出液体的折射率。 （2）注意在 近轴条件下的近似，再通过几何知识即可求解。 解：（1）主轴上物 A 发出的光线 AB ，经液体界面折射后沿 BD 方向入射球面镜 时，只要 BD 延长线过球心 C，光线经球面反射后必能沿原 路折回。按光的可逆性原理，折回的光线相交于 A （图 33-100）。 对空气、液体界面用折射定律有 R2 OC E R 图 33-99 A C E O B D i r i 图 33-100 rni sinsin CBBE ABBE r in / / sin sin 当光圈足够小时， EB ，因此有 33.1 0.30 0.40 AE CEn (2) 先考虑主轴上点物 A 发出的两条光线，其一沿主轴方向 ACOE 入射界 面，无偏折地出射，进入人眼 E。其二沿 AP 方向以入射角 i 斜入射界面 P 点， 折射角为 r。折射光线 PQ 要能进入人眼 E，P 点应非常靠近 O 点，或者入射角 i 和折射角 r 应很小。若角度以弧度量度，在小角（近轴）近似下，折射定律 rin sinsin 可写为 nir 。这两条光线反向 延长， 在主轴上相交于 A ，A 即为物 A 之虚 像点（图 33-101）。 对 AAP 用正弦定律，得 PA i PA i AA PAA sin)sin(sin 在小角（近轴）近似下： iiiniPAAPAA sin,sin OAPA 上式可写为 OA i ROA ini 2 解上式得 RR n ROA 4 2/32 2 2 2 为了分析成像倒立和放大情况，将水银柱看成有一定高度的垂轴小物体 AB ，即 然 AA ~ 是一对共轭点，只要选从 B 发出的任一条光线经界面折射后，反 A B A B i C n P Q O E i nir 图 33-101 向延长线与过 A 点垂轴线相交于 B ， B 是点物 B 虚像点，即 BA 是物 AB 之正立虚像。 选从 B 点发出过圆柱面轴心 C 的光线 BC。该光线对界面来说是正入射 （入射角 为零），故无偏折地出射， 反向延长 BC 线交过 A 垂轴线于 B ，从 CBA ∽ ΔABC 得 放大率 33 R R AC CA AB BA 9．如图 41-83所示， 两个固定的均匀带电球面 A 和 B 分别带电 4Q和 Q（Q>0）。 两球心之间的距离 d 远大于两球的半径，两球心的连线 MN 与两球面的相交处 都开有足够小的孔， 因小孔而损失的电量可以忽略不计。 一带负电的质点静止地 放置在 A 球左侧某处 P 点，且在 MN 直线上。设质点从 P 点释放后刚好能穿越 三个小孔，并通过 B 球的球心。试求质点开始时所在的 P 点与 A 球球心的距离 x 应为多少？ 分析： 质点释放后，由于质点带负电， A 球和 B 球带正电，故质点先加速，穿过 A 球内时，不受 A 球的电场力作用，但仍受 B 球的电场力，进一步加速。在两球之间时， 存在一质点所受合力为零的点， 设此点为 S， 且由于 A 球所带电量大于 B 球带电量， S 点应离 B 球较近。所以质点从 A 球内 出来后到 S 点这段距离内作减速运动，从 S 点到 B 球的第一个孔这段距离内作 加速运动。因此，为了使质点能到达 B 球的球心，第一个必要条件是，质点必 须通过 S 点， 即质点在 S 点的速度至少应大于零或至少等于零。 若质点能通过 S x d M N A B QQ4 P 图 41-83 点，则如上述，从 S 点到 B 球的第一个孔期间，质点沿 MN 向右加速。由于质 点在 B 球内不受 B 球的电场力作用，但仍受 A 球向左的引力，质点减速，因此 为了使用期质点能通过 B 球的球心，第二个必要条件是，质点在 B 球球心处的 速度应大于零或至少等于零。 本题的关键在于带电体系的电势能与带电质点的动能之和， 在该质点运动过 程中守恒。因此质点刚好能通过 S 点的条件可表示为，质点在 P 点和 S 点时， 带电体系的电势能相等（注意，质点在 P 点静止） 。同样，若质点在 S 点时带电 体系的电势能大于（或等于）质点在 B 球球心时带电体系的电势能，则表明质 点若能通过 S 点，就必定能通过（或刚好到达） B 球球心。 解： 根据分析，在 MN 直线上在 A 球和 B 球之间有一个 S 点，带电质点在 S 点受力为零。设 S 点与 A 球和 B 球球心的距离为 1r 和 2r ，则 2 2 2 1 4 r Qk r Qk drr 21 由以上两式，可解出 drdr 3 1; 3 2 21 带电质点从 P 点静止释放后，刚好能够到达 S 点的条件是，它在 P 点和 S 点的电势能相等，即 21 44 r qQk r qQk dx qQk x qQk 式中 -q(q>0)是带电质点的电量。把上面解出的 1r 和 2r 代入，得 dx 110 9 2 为了判断带电质点刚好到达 S 点后，能否通过 B 球球心，需比较它在 S 点 的电势能 SW 与它在 B 球球心处的电势能 BW 的大小，因 d Qqk r qQk r qQkWS 94 21 B B Rd k Q q r qQk r qQkW 144 21 式中 BR 为 B 球的半径。由题设 BR ?d 故 dRd B 914 即 SB WW 因此，带电质点只要能到达 S 点，就必定能通过 B 球球心。于是，所求开 始时 P 点与 A 球球心的距离 x 即为上述结果，即 dx 110 9 2 10．如图 41-88 所示，在真空中有 4 个半径为 a 的不带电的相同导体球，球 心分别位于边长为 r（r?a）的正方形的四个顶点上。首先，让球 1 带电荷 Q（Q? 0），然后取一细金属丝，其一端固定于球 1 上，另一端分别依次与球 2、3、4、 大地接触， 每次接触时间都足以使它们达到静电平衡。 设分布在细金属丝上的电 荷可忽略不计。试求流入大地的电量的表达式。 解： 当球 1 与球 2 连接后，用 1Q 和 Q2 分别表示球 1 和球 2 上的电量，可得 2/12 QQQ 。球 1 与球 3 连接后，因球 1 和 球 3 处于对称位置， 其电量 1Q 和 Q3 相等， 故可得 .4/13 QQQ 球 1 与球 4 连接后， 电荷分布呈不对称状态， 设连接后球 1 和球 4 上的电量分别 为 Q1 与 Q4。它们可利用等电势方法求出，即 rkQrkQrkQakQU /2/// 43211 akQrkQrkQakQU //2// 43214 以上各式中，计算各球上的电荷在另一球处引起的电势时，利用了 r?a 的条 件。由于 41 UU ，且 ,4/141 QQQQ 故 8/2/1211 araQQ 8/2/1214 araQQ 利用 r?a 的条件，略去二阶小量，上式可写成 8/2/1211 raQQ 8/2/1214 raQQ 最后将球 1 与球 4 断开并把球 1 接地。 设接地后球 1 所带电量为 q1，电势为 1U ，则球 1 的电势为 图 41-88 B A a b d D l 0/2// 43211 rkQrkQrkQakQU rQQQaq /2/ 4321 rraaQ /28/1224/18/5 raQ /24/18/5 此时球 1 上带负电，故流入大地的电量 入地Q 为 11 qQQ入地 raQraQ /24/18/58/2/121 8//2/21251 raQ 8//2/2341 raQ 答： . 2 234 1 8 r a Q 。