【物理】2018届二轮复习圆锥摆模型及其拓展应用学案（全国通用）

【物理】2018届二轮复习圆锥摆模型及其拓展应用学案（全国通用）

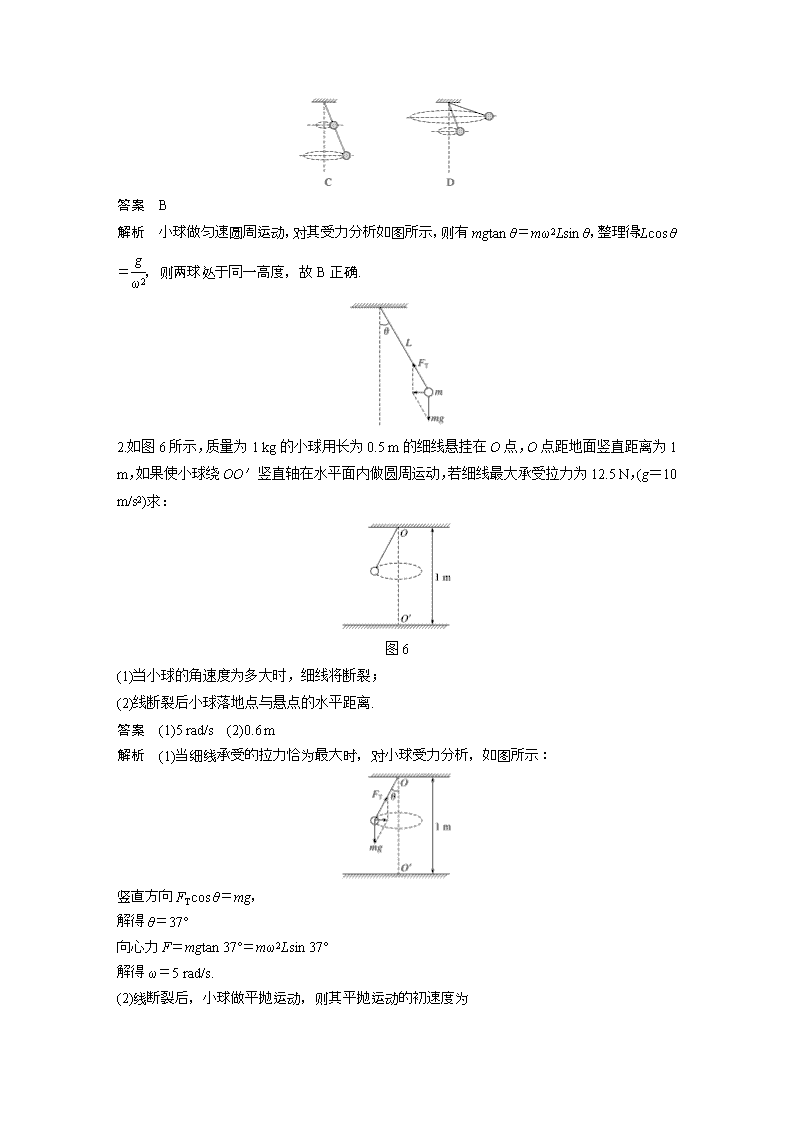
第8点　圆锥摆模型及其拓展应用 ‎(1)圆锥摆结构和运动模型 如图1所示，一根不可伸长的绳，一端固定在O1点，另一端拴一小球(可视为质点)，给小球一水平初速度，不计空气阻力，小球在水平面内做匀速圆周运动.‎ 图1‎ ‎(2)提供的向心力：‎ ‎①可认为绳子对小球的拉力和小球的重力的合力提供向心力.‎ ‎②也可认为是绳子拉力在水平方向的分量提供向心力.‎ ‎(3)线速度和绳长的关系：(如图2所示)‎ 图2‎ 设小球的质量为m，悬线与竖直方向的夹角为θ，绳长为l，则小球做圆周运动的半径为r＝lsin θ.由牛顿第二定律得mgtan θ＝m.‎ 所以v＝＝.‎ ‎(4)拓展：①光滑漏斗上小球的圆周运动.如图3.‎ ‎②火车转弯问题.如图4.‎ ‎　　‎ ‎　　　　 图3　　　　　　　图4‎ 对点例题　长为L的细线，一端固定于O点，另一端拴一质量为m的小球，让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动)，如图5所示，摆线与竖直方向的夹角为α，求：‎ 图5‎ ‎(1)线的拉力大小；‎ ‎(2)小球运动的线速度的大小；‎ ‎(3)小球运动的周期.‎ 解题指导　对小球受力分析如图所示，小球受重力mg和线的拉力FT作用，这两个力的合力mgtan α指向圆心，提供向心力，由受力分析可知，细线拉力FT＝.由F＝m＝mω2R＝m＝mgtan α，半径R＝Lsin α，得v＝ ＝ sin α，T＝2π .‎ 答案　见解题指导 ‎1.两根长度不同的细线下面分别悬挂两个小球，细线上端固定在同一点，若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动，则两个小球在运动过程中，相对位置关系示意图正确的是(　　)‎ 答案　B 解析　小球做匀速圆周运动，对其受力分析如图所示，则有mgtan θ＝mω2Lsin θ，整理得：Lcos θ＝，则两球处于同一高度，故B正确.‎ ‎2.如图6所示，质量为1 kg的小球用长为0.5 m的细线悬挂在O点，O点距地面竖直距离为1 m，如果使小球绕OO′竖直轴在水平面内做圆周运动，若细线最大承受拉力为12.5 N，(g＝10 m/s2)求：‎ 图6‎ ‎(1)当小球的角速度为多大时，细线将断裂；‎ ‎(2)线断裂后小球落地点与悬点的水平距离.‎ 答案　(1)5 rad/s　(2)0.6 m 解析　(1)当细线承受的拉力恰为最大时，对小球受力分析，如图所示：‎ 竖直方向FTcos θ＝mg，‎ 解得θ＝37°‎ 向心力F＝mgtan 37°＝mω2Lsin 37°‎ 解得ω＝5 rad/s.‎ ‎(2)线断裂后，小球做平抛运动，则其平抛运动的初速度为 v0＝ωLsin 37°＝1.5 m/s 竖直方向：y＝h－Lcos 37°＝gt2‎ 水平方向：x＝v0t 解得d＝＝0.6 m.‎