- 2021-05-14 发布 |
- 37.5 KB |
- 36页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广东省广州市高考数学考前查漏补缺题理科20105
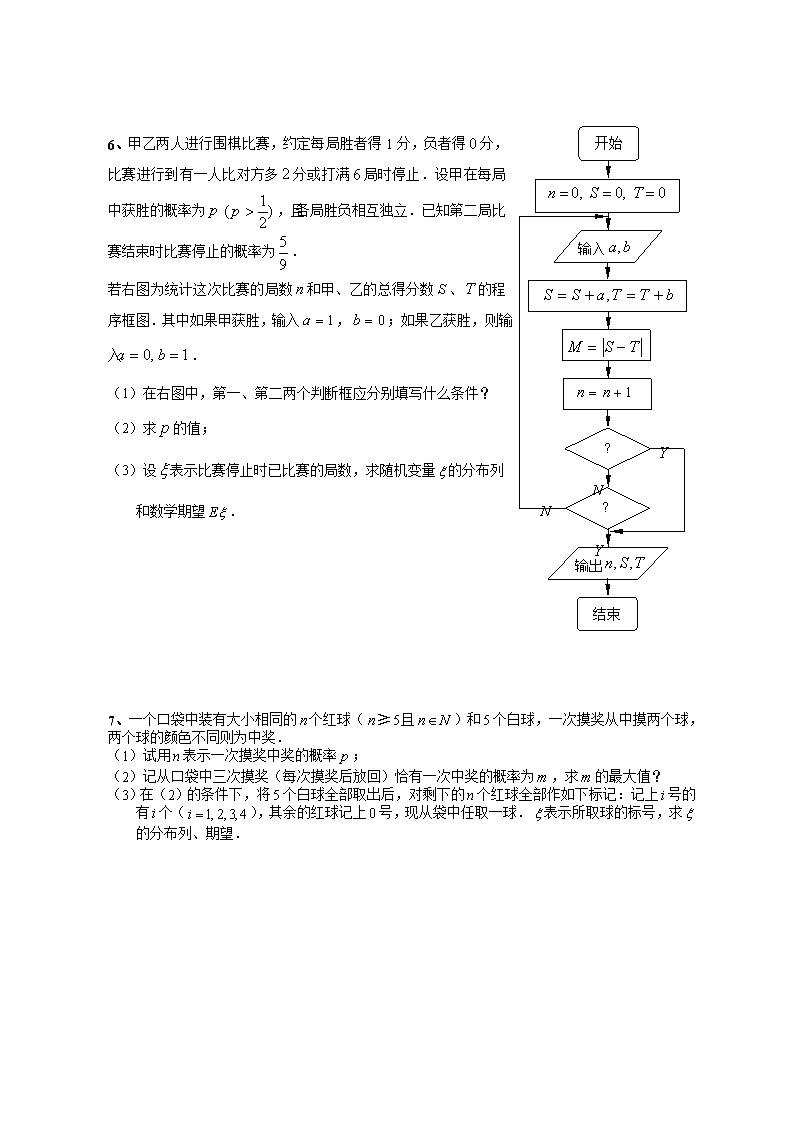
2010年广州市高考数学考前查漏补缺题 (理 科) 说明: ⒈ 本训练题由广州市中学数学教学研究会高三中心组组织编写,共28题,分为A,B两组,其中B组题较难. ⒉ 本训练题仅供本市高三学生考前查漏补缺用,希望在5月31日之前完成. 3.本训练题与市高三质量抽测、一模、二模等数学试题在内容上相互配套,互为补充.四套试题覆盖了高中数学的主要知识和方法.因此,希望同学们在5月31日至6月6日之间,安排一段时间,对这四套试题进行一次全面的回顾总结,同时,将高中数学课本中的基本知识(如概念、定理、公式等)再复习一遍. 希望同学们保持良好的心态,在高考中稳定发挥,考取理想的成绩! A 组 1、已知函数,R. (1)求它的振幅、周期、初相; (2)用五点法作出它的简图; (3)该函数的图象可由(R)的图象经过怎样的平移和伸缩变换得到? 2、已知两个向量,,其中,且满足. (1)求的值; (2)求的值. 3、在△中,内角,,对边的边长分别是,已知. (1)若△的面积等于,求,; (2)若,求△的面积. 4、一缉私艇发现在方位角(从正北方向顺时针转到目标方向线的水平角)45°方向,距离15 海里的海面上有一走私船正以25 海里/小时的速度沿方位角为105°的方向逃窜.若缉私艇的速度为35 海里/小时,缉私艇沿方位角为45°+α的方向追去,若要在最短时间内追上该走私船. (1)求角α的正弦值; (2)求缉私艇追上走私船所需的时间. 1 2 3 10 20 30 40 50 参加人数 活动次数 5、某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. (1)求合唱团学生参加活动的人均次数; (2)从合唱团中任意选两名学生,求他们参加活动次 数恰好相等的概率; (3)从合唱团中任选两名学生,用表示这两人参加 活动次数之差的绝对值,求随机变量的分布列及 数学期望. 输入 开始 结束 输出 6、甲乙两人进行围棋比赛,约定每局胜者得1分,负者得分,比赛进行到有一人比对方多分或打满局时停止.设甲在每局中获胜的概率为,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为. 若右图为统计这次比赛的局数和甲、乙的总得分数、的程序框图.其中如果甲获胜,输入,;如果乙获胜,则输入. (1)在右图中,第一、第二两个判断框应分别填写什么条件? (2)求的值; (3)设表示比赛停止时已比赛的局数,求随机变量的分布列 和数学期望. 7、一个口袋中装有大小相同的个红球(且)和个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖. (1)试用表示一次摸奖中奖的概率; (2)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为,求的最大值? (3)在(2)的条件下,将个白球全部取出后,对剩下的个红球全部作如下标记:记上号的有个(),其余的红球记上号,现从袋中任取一球.表示所取球的标号,求的分布列、期望. 8、面积为的正方形中有一个不规则的图形,可按下面方法估计的面积:在正方形中随机投掷个点,若个点中有个点落入中,则的面积的估计值为,假设正方形的边长为2,的面积为1,并向正方形中随机投掷个点,以表示落入中的点的数目. (1)求的均值; (2)求用以上方法估计的面积时,的面积的估计值与实际值之差在区间内的概率. 附表: 9、三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. (1)证明:AC⊥SB; (2)求二面角N-CM-B的一个三角函数值; (3)求点B到平面CMN的距离. 10、如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形. 图3 L E M N F 图1 侧视图 主视图 图2 P C A P C D 图1 (1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积. (2)图3中,L、E均为棱PB上的点,且,,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由. 11、已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) . (1)当x=2时,求证:BD⊥EG ; (2)若以F、B、C、D为顶点的三棱锥的体积记为f(x), 求f(x)的最大值; (3)当 f(x)取得最大值时,求二面角D-BF-C的余弦值. 12、如图,在梯形中,∥,,, M F E C D B A 平面平面,四边形是矩形,,点在线段上. (1)求证:平面; (2)当为何值时,∥平面?证明你的结论; (3)求二面角的平面角的余弦值. 13、已知直线所经过的定点恰好是椭圆的一个焦点,且椭圆上的点到点的最大距离为8. (1)求椭圆的标准方程; (2)已知圆,,直线.试证明:当点在椭圆C上运动时,直线与圆恒相交,并求直线被圆所截得弦长的取值范围. 14、已知椭圆中心在原点,焦点在y轴上,离心率为,以原点为圆心,椭圆短半轴长为半径的圆与直线相切. (1)求椭圆的标准方程; (2)设点F是椭圆在y轴正半轴上的一个焦点,点A,B是抛物线上的两个动点,且满足,过点A,B分别作抛物线的两条切线,设两切线的交点为M,试推断是否为定值?若是,求出这个定值;若不是,说明理由. 15、已知椭圆:,其焦距为2c,若(≈0.618),则称椭圆为“黄金椭圆”. (1)求证:在黄金椭圆:中,、、成等比数列; (2)黄金椭圆:的右焦点为,椭圆上是否存在一点P,使得过点F2、P的直线的与轴的交点满足?若存在,求直线的斜率;若不存在,请说明理由; (3)在黄金椭圆中有真命题:已知黄金椭圆:的左、右焦点分别是、,以、、、为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明. 16、已知椭圆:的右顶点为,过的焦点且垂直长轴的弦长为. (1)求椭圆的方程; (2)设点在抛物线:上,在点处的 切线与交于点.当线段的中点与的中点的横 坐标相等时,求的最小值. 17、设数列的前项和为,且. (1) 求; (2) 求数列的通项公式. 18、已知数列满足,().. (1)判断数列是否为等比数列?若不是,请说明理由;若是,试求出通项;. (2)如果时,数列的前项和为,试求出. 19、已知函数 (1)求; (2)已知数列满足,,求数列的通项公式; (3)求证:. 20、某企业自年月日正式投产,环保监测部门从该企业投产之日起对它向某湖区排放污水进行了四个月的跟踪监测,检测的数据如下表.并预测,如果不加以治理,该企业每月向湖区排放污水的量将成等比数列. 月份 月 月 月 月 该企业向湖区排放的污水(单位:立方米) 万 万 万 万 (1)如果不加以治理,求从年月起,个月后,该企业总计向某湖区排放了多少立方米的污水? (2)为保护环境,当地政府和企业决定从7月份开始投资安装污水处理设备,预计月份的污水排放量比月份减少万立方米,以后每月的污水排放量均比上月减少万立方米,当企业停止排放污水后,再以每月万立方米的速度处理湖区中的污水,请问什么时候可以使湖区中的污水不多于万立方米? 21、已知aÎR,函数f(x)=x2| x-a |. (1)当a=2时,求使f(x)=x成立的的集合; (2)求函数y=f(x)在区间上的最小值. 22、已知函数在上是增函数,在上是减函数,函数在上有三个零点,且2是其中一个零点. (1)求的取值范围; (2)试探究直线与函数的图像交点个数的情况,并说明理由. 23、设函数,其中. (1)若曲线在处的切线与轴平行,求实数的值; (2)若,证明:对任意的正整数,不等式都成立. 24、已知是实数,函数当时, (1)证明: (2)证明:当时, (3)设当时,的最大值为2,求. B 组 25、设正项数列对一切正整数均有,如果,. (1)求,的值; (2)求数列的通项公式; (3)设数列前项之积为,试比较与的大小,并证明你的结论. 26、已知函数,设在点N*)处的切线在轴上的截距为,数列满足:N*). (1)求数列的通项公式; (2)在数列中,仅当时,取最小值,求的取值范围; (3)令函数,数列满足:,N*),求证:对于一切的正整数,都满足:. 27、已知定义在上的函数满足: ,且对于任意实数,总有成立. (1)求的值,并证明函数为偶函数; (2)若数列满足,求证:数列为等比数列; (3)若对于任意非零实数,总有.设有理数满足,判断和 的大小关系,并证明你的结论. 28、已知 f(x)= a x 2 + bx + c(a > 0 且 b≠0). (1)若 | f(0)| = | f(1)| = | f(-1)| = 1,试求 f(x)的解析式和 f(x)的最小值; (2)已知f(x)的对称轴方程是x = 1,当 f(x)的图象在 x 轴上截得的弦长不小于 2 时,试求 a、b、c 满足的条件; (3)若| f(0)|≤1,| f(1)|≤1,| f(-1)|≤1,证明:当 x Î [-1,1] 时,有 | f(x)|≤. 2010年广州市高考数学考前查漏补缺(理 科)参考答案 A组 1、解:(1)函数的振幅为,周期为,初相为. (2)列表: 0 0 0 画简图: (3)解法1: 向左平移个单位 函数的图象 函数的图象, 各点的横坐标缩短到原来的(纵坐标不变) 函数的图象, 各点的纵坐标缩短到原来的(横坐标不变) 函数的图. 各点的横坐标缩短到原来的(纵坐标不变) 向左平移个单位 解法2:函数的图象 各点的纵坐标缩短到原来的(横坐标不变) 函数的图像 函数的图象 函数的图象. 2、解:(1), 所以. (2)因为,所以, 结合,可得. 于是, . 3、解:(1)由余弦定理及已知条件,得. 又因为△的面积等于,所以,得. 联立方程组解得 (2)由题意,得,即. 当,即时,,,, 此时△的面积. 当时,得,由正弦定理,得. 联系方程组解得此时△的面积. 所以△的面积. 4、解:(1)设缉私艇追上走私船所需的时间为t小时, 则有|BC|=25t,|AB|=35t, 且∠CAB=α,∠ACB=120°, 根据正弦定理得: ,即, ∴ sinα=. (2)在△ABC中由余弦定理得: |AB|2=|AC|2+|BC|2-2|AC||BC|cos∠ACB, 即 (35t)2=152+(25t)2-2·15·25t·cos120°, 即24t2―15t―9=0, 解之得:t=1或t=-(舍) 故缉私艇追上走私船需要1个小时的时间. 5、解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40. (1)该合唱团学生参加活动的人均次数为. (2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为. (3)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件,“这两人中一人参加2次活动,另一人参加3次活动”为事件,“这两人中一人参加1次活动,另一人参加3次活动”为事件.易知 ;; 的分布列: 0 1 2 P 的数学期望:. 6、解:(1)程序框图中的第一个条件框应填,第二个应填. (注意:答案不唯一.如:第一个条件框填,第二个条件框填,或者第一、第二条件互换.都可以.) (2)依题意,当甲连胜局或乙连胜局时,第二局比赛结束时比赛结束. 有. 解得或. , . (3)解法一:依题意知,的所有可能值为2,4,6. 设每两局比赛为一轮,则该轮结束时比赛停止的概率为. 若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响. 从而有, , . 随机变量的分布列为: 故. 解法二:依题意知,的所有可能值为2,4,6. 令表示甲在第局比赛中获胜,则表示乙在第局比赛中获胜. 由独立性与互不相容性得 , , . 随机变量的分布列为: 故. 7、解:(1)一次摸奖从个球中任取两个,有种方法. 它们是等可能的,其中两个球的颜色不同的方法有种, 一次摸奖中奖的概率为. (2)设每次摸奖中奖的概率为,三次摸奖中恰有一次中奖的概率是: (). 对的导数 因而在上为增函数,在上为减函数. ∴当,即,时,. (3)由(2)知:记上号的有个红球,从中任取一球,有种取法,它们是等可能的.故的分布列是: . 8、解:每个点落入中的概率均为.依题意知. (1). (2)依题意所求概率为, . 9、解法一:(1)取AC中点D,连结SD、DB. ∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD,SD∩DB=D. ∴AC⊥平面SDB,又SB平面SDB, ∴AC⊥SB. (2)交于AC. 取BD中点E,N为SB的中点,. NE⊥平面ABC, 过E作EF⊥CM于F,连结NF,则NF⊥CM.∴∠NFE为二面角N-CM-B的平面角. ∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC. 又∵NE⊥平面ABC,∴NE∥SD. ∵SN=NB,∴NE=SD===, 且ED=EB.在正△ABC中,由平几知识可求得EF=MB=, 在Rt△NEF中,tan∠NFE==2. (3)在Rt△NEF中,NF==, ∴S△CMN=CM·NF=,S△CMB=BM·CM=2. 设点B到平面CMN的距离为h,∵VB-CMN=VN-CMB, NE⊥平面CMB, ∴S△CMN·h=S△CMB·NE,∴h==. 即点B到平面CMN的距离为. 解法二:(1)取AC中点O,连结OS、OB. ∵SA=SC,AB=BC,∴AC⊥SO且AC⊥BO. ∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC ∴SO⊥面ABC,∴SO⊥BO. ...........2分 如图所示建立空间直角坐标系O-xyz.则A(2,0,0),B(0,2,0),C(-2,0,0), S(0,0,2),M(1,,0),N(0,,). ∴=(-4,0,0),=(0,2,-2), ∵·=(-4,0,0)·(0,2,-2)=0, ∴AC⊥SB. (2)由(1)得=(3,,0),=(-1,0,). 设n=(x,y,z)为平面CMN的一个法向量,则 ·, 取,∴=(,-,1), ·, 又=(0,0,2)为平面ABC的一个法向量,∴==. 由图知的夹角即为二面角N-CM-B的大小,其余弦值为. (3)由(1)(2)得=(-1,,0),=(,-,1)为平面CMN的一个法向量, ∴点B到平面CMN的距离即为上射影的绝对值=. 10、解:(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形(如右图). 其面积为:6×6=36(cm2). (注:图正确,面积计算体现了图形为正方形一样给分) z (2)以C为原点,CD为x轴,CB为y轴,CP为z轴建立空间直角坐标系(图略),则D(6,0,0),A(6,6,0),B(0,6,0),P(0,0,6),E(0,3,3),L(0,1,5),M(3,3,3),N(3,0,3), ∴ 设平面LMN的法向量为=(x,y,z) 由 得令x=2 则=(2,0,3), 设,(), 则, 由,得,即=, 又,点F在AC上.EF 所以,EF//平面LMN. 即在底面正方形的对角线AC上存在符合题意的点F,CF=AC=cm. x y z 11、(1)方法一:∵平面平面, AE⊥EF,∴AE⊥平面,AE⊥EF,AE⊥BE, 又BE⊥EF,故可如图建立空间坐标系E-xyz. ,又为BC的中点,BC=4, .则A(0,0,2),B(2,0,0),G(2,2,0), D(0,2,2),E(0,0,0), (-2,2,2),(2,2,0), (-2,2,2)(2,2,0)=0,∴. 方法二:作DH⊥EF于H,连BH,GH, 由平面平面知:DH⊥平面EBCF, 而EG平面EBCF,故EG⊥DH. 为平行四边形,且 H ,四边形BGHE为正方形,∴EG⊥BH,BHDH=H, 故EG⊥平面DBH, 而BD平面DBH,∴ EG⊥BD. (或者直接利用三垂线定理得出结果) (2)∵AD∥面BFC, 所以 =VA-BFC= , 即时有最大值为. (3)设平面DBF的法向量为,∵AE=2, B(2,0,0),D(0,2,2), H _ E M F D B A C G F(0,3,0),∴ (-2,2,2), 则 , 即, 取,∴ ,面BCF一个法向量为, 则cos<>=, 由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-. 12、(1)在梯形中,, 四边形是等腰梯形,且,. 又平面平面,交线为,平面. (2)解法一:当时,平面, 在梯形中,设,连接,, , ,而,. ,四边形是平行四边形,. 又平面,平面平面. x D y z C O F B A E 解法二:当时,平面,由(Ⅰ)知,以点为原点,所在直线为坐标轴,建立空间直角坐标系, 则,,,, , 平面, 平面与、共面, 也等价于存在实数、,使, 设, 又,, 所以:成立,解得(过程略), 当时,平面. (3)解法一:取中点,中点,连结,,DH , 平面又,,,又, 是二面角的平面角. 在中,, ,,. 又, 在中,由余弦定理得, x D y z C O F B A E 即二面角的平面角的余弦值为. 解法二:由(1)知,以点为原点,所在直线为坐标轴,建立空间直角坐标系,则,,,, ,, 设为平面DEF的法向量,. 设为平面BEF的法向量,, ∴,即所求角的余弦值为. 13、解:(1)由得,, 所以直线过定点(3,0),即 设椭圆的方程为, 则,解得,所以椭圆的方程为. (2)因为点在椭圆上运动,所以, 从而圆心到直线的距离 所以直线与圆恒相交. 又直线被圆截得的弦长, 由于,所以,则, 即直线被圆截得的弦长的取值范围是. 14、解:(1)设椭圆方程为(a>b>0). 因为,得.又,则. 故椭圆的标准方程是. (2)由椭圆方程知,c=1,所以焦点F(0,1),设点A(x1,y1),B(x2,y2). 由,得(-x1,1-y1)=λ(x2,y2-1),所以-x1=λx2,1-y1=λ(y2-1). 于是.因为,,则y1=λ2y2. 联立y1=λ2y2和1-y1=λ(y2-1),得y1=λ,y2=. 因为抛物线方程为y=x2,求导得y′=x.设过抛物线上的点A、B的切线分别为l1,l2,则直线l1的方程是y=x1(x-x1)+y1,即y=x1x-x12. 直线l2的方程是y=x2(x-x2)+y2,即y=x2x-x22. 联立l1和l2的方程解得交点M的坐标为. 因为x1x2=-λx22=-4λy2=-4. 所以点M. 于是,(x2-x1,y2-y1). 所以==(x22-x12)-2(x22-x12)=0. 故为定值0. 15、(1)证明:由及,得, 故、、成等比数列. (2)解:由题设,显然直线垂直于轴时不合题意,设直线的方程为, 得,又,及,得点的坐标为, 因为点在椭圆上,所以,又,得, ,故存在满足题意的直线,其斜率. (3)黄金双曲线的定义:已知双曲线:,其焦距为,若(或写成),则称双曲线为“黄金双曲线”. 在黄金双曲线中有真命题:已知黄金双曲线:的左、右焦点分别是、,以、、、为顶点的菱形的内切圆过顶点、. 证明:直线的方程为,原点到该直线的距离为, 将代入,得,又将代入,化简得, 故直线与圆相切,同理可证直线、、均与圆相切,即以、为直径的圆为菱形的内切圆,命题得证. 16、解:(1)由题意得所求的椭圆方程为. (2)不妨设 则抛物线在点P处的切线斜率为,直线MN的方程为, 将上式代入椭圆的方程中,得, 即, 因为直线MN与椭圆有两个不同的交点,所以有, 设线段MN的中点的横坐标是,则, 设线段PA的中点的横坐标是,则, 由题意得,即有, 其中的或; 当时有,因此不等式不成立; 因此,当时代入方程得, 将代入不等式成立, 因此的最小值为1. 17、解:(1) 容易求得:. (2)方法一:猜想, 下用数学归纳法证明. ① 当时, ,结论成立. ② 假设当时,结论成立,即,则当时, ,即时结论也成立. 由①、②知对一切,. 方法二:∵ ① ∴ ② ②①,得,即. 令,则, 比较系数,得,故, ∴数列是首项为,公比为的等比数列, ∴,即. 18、解:(1), .令,则,且. ∴当时,,则,数列不是等比数列. 当时,,则数列是等比数列,且公比为2. ,即.解得. (2)由(1)知,当时,,. 由错位相减法,求得, ∴. 19、解:(1)因为 所以设S= ① S= ② ①+②得: =, 所以S=3012. (2)由两边同减去1,得 所以, 所以,是以2为公差以为首项的等差数列, 所以 (3)证法一:数学归纳法. ① 当时,,不等式成立; ② 假设当时不等式成立,即,则当时, ,即当时不等式也成立. 由①②知,对一切,都有. 证法二:放缩法. ∵,∴,∴, 则,所以,. 20、解:(1) 由题意知:企业每月向湖区排放的污水量成等比数列, 设第一个月污水排放量为,则,公比为,则第个月的污水排放量为,如果不治理,个月后的污水总量为: (万立方米). (2)由(1)知,则,由题意知,从月份开始,企业每月向湖区排放的污水量成等差数列,公差为,记7月份企业向湖区排放的污水量为,则 ,令, 所以该企业年月向湖区停止污水排放, 则该企业共排污水(万立方米). 设个月后污水不多于万立方米,则. 因为,所以个月后即年月污水不多于万立方米. 21、解:(1)当a=2时,f(x)=x2| x-2 |. 当x<2时,由f(x)=x2(2-x) =x,解得x=0或x=1; 当x≥2时,由f(x)=x2( x-2 )=x.,解得x=1+. 综上所述,使f(x)=x成立的的集合为{0,1,1+}. (2)①当a≤1时,在区间[1,2]上,f(x)= x2(x-a)=x3-ax2. 因为当1≤x≤2时,=3x2-2ax=3x(x-a)>0, 所以f(x)在[1,2]上单调递增,所以=f(1)=1-a. ②当1查看更多
相关文章
- 当前文档收益归属上传用户