2020年全国Ⅰ卷高考文数真题试卷（含答案）

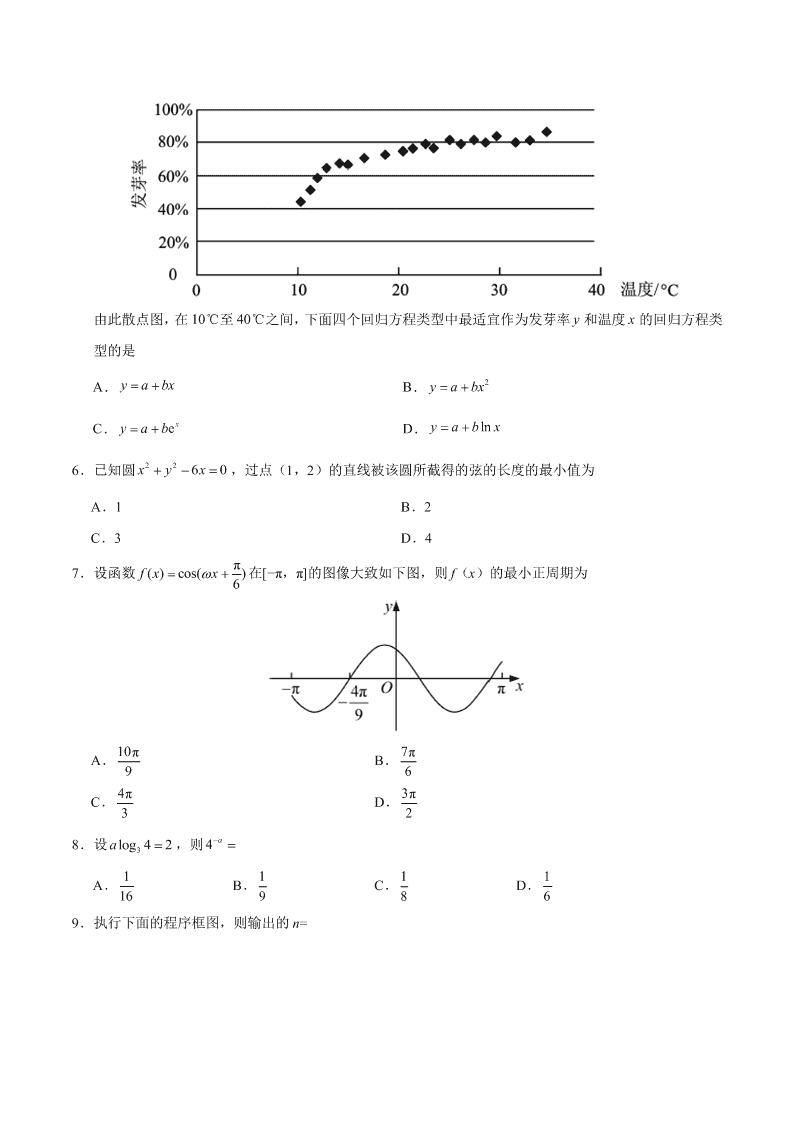
2020年全国Ⅰ卷高考文数真题试卷（含答案）

2020 年全国Ⅰ卷高考文数真题试卷（含答案） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合题目 要求的。 1．已知集合 2{|340},{4,1,3,5}AxxxB ，则 AB A． { 4 ,1} B． {1,5} C． {3,5} D． {1,3} 2．若 31 2 i iz    ，则 | | =z A．0 B．1 C． 2 D．2 3．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方 形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为 A． 51 4  B． 51 2  C． 51 4  D． 51 2  4．设 O 为正方形 ABCD 的中心，在 O，A，B，C，D 中任取 3 点，则取到的 3 点共线的概率为 A． 1 5 B． 2 5 C． 1 2 D． 4 5 5．某校一个课外学习小组为研究某作物种子的发芽率 y 和温度 x（单位：℃）的关系，在 20 个不同的温 度条件下进行种子发芽实验，由实验数据( , )( 1,2, ,20)iix y i  得到下面的散点图： 由此散点图，在 10℃至 40℃之间，下面四个回归方程类型中最适宜作为发芽率 y 和温度 x 的回归方程类 型的是 A． y a b x B． 2y a bx C． e xy a b D． lny a b x 6．已知圆 2260x y x   ，过点（1，2）的直线被该圆所截得的弦的长度的最小值为 A．1 B．2 C．3 D．4 7．设函数 π()cos() 6fxx 在[−π，π]的图像大致如下图，则 f（x）的最小正周期为 A．10π 9 B． 7π 6 C． 4 π 3 D． 3 π 2 8．设 3log 4 2a  ，则 4 a  A． 1 16 B． 1 9 C． 1 8 D． 1 6 9．执行下面的程序框图，则输出的 n= A．17 B．19 C．21 D．23 10．设 {}na 是等比数列，且 123 1a a a， 234 +2a a a，则 678a a a A．12 B．24 C．30 D．32 11．设 12,FF是双曲线 2 2:13 yCx的两个焦点，O 为坐标原点，点 P 在 C 上且 | | 2OP  ，则 12P F F△ 的 面积为 A． 7 2 B．3 C． 5 2 D．2 12．已知 ,,A B C 为球O 的球面上的三个点，⊙ 1O 为 ABC△ 的外接圆，若⊙ 的面积为 4 π ， 1ABBCACOO ，则球 的表面积为 A． 64 π B． 48 π C． 36 π D． 32 π 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．若 x，y 满足约束条件 220, 10, 10, xy xy y      则 z=x+7y 的最大值为 . 14．设向量 (1, 1), ( 1,2 4)mm    ab ，若 ab，则 m  . 15．曲线 ln 1y x x   的一条切线的斜率为 2，则该切线的方程为 . 16．数列{}na 满足 2 ( 1) 3 1n nna a n     ，前 16 项和为 540，则 1a  . 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题，每个试题考生 都必须作答。第 22、23 题为选考题，考生根据要求作答。 （一）必考题：共 60 分。 17．（12 分） 某厂接受了一项加工业务，加工出来的产品(单位：件)按标准分为 A，B，C，D 四个等级.加工业务约 定：对于 A 级品、B 级品、C 级品，厂家每件分别收取加工费 90 元，50 元，20 元；对于 D 级品，厂 家每件要赔偿原料损失费 50 元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为 25 元/件， 乙分厂加工成本费为 20 元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了 100 件这 种产品，并统计了这些产品的等级，整理如下： 甲分厂产品等级的频数分布表 等级 A B C D 频数 40 20 20 20 乙分厂产品等级的频数分布表 等级 A B C D 频数 28 17 34 21 （1）分别估计甲、乙两分厂加工出来的一件产品为 A 级品的概率； （2）分别求甲、乙两分厂加工出来的 100 件产品的平均利润，以平均利润为依据，厂家应选哪个分厂 承接加工业务? 18．（12 分） ABC△ 的内角 A，B，C 的对边分别为 a，b，c.已知 B=150°. （1）若 a= 3 c，b=2 7 ，求 的面积； （2）若 sinA+ sinC= 2 2 ，求 C. 19．（12 分） 如图， D 为圆锥的顶点， O 是圆锥底面的圆心， 是底面的内接正三角形， P 为 DO 上一点， ∠APC=90°． （1）证明：平面 PAB⊥平面 PAC； （2）设 DO= 2 ，圆锥的侧面积为 3π ，求三棱锥 P−ABC 的体积. 20．（12 分） 已知函数 ()e(2) xfxax  . （1）当 1a  时，讨论 ()fx的单调性； （2）若 有两个零点，求 a 的取值范围. 21．（12 分） 已知 A、B 分别为椭圆 E： 2 2 2 1x ya （a>1）的左、右顶点，G 为 E 的上顶点， 8AGGB，P 为直 线 x=6 上的动点，PA 与 E 的另一交点为 C，PB 与 E 的另一交点为 D． （1）求 E 的方程； （2）证明：直线 CD 过定点. （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题计分。 22．[选修 4—4：坐标系与参数方程]（10 分） 在直角坐标系 xOy 中，曲线 1C 的参数方程为 cos , sin k k xt yt    (t 为参数 ) ．以坐标原点为极点， x 轴正半轴为 极轴建立极坐标系，曲线 2C 的极坐标方程为 4 cos 16 sin 3 0      ． （1）当 1k  时， 是什么曲线？ （2）当 4k  时，求 与 的公共点的直角坐标． 23．[选修 4—5：不等式选讲]（10 分） 已知函数 ( ) | 3 1| 2 | 1|f x x x    ． （1）画出 ()y f x 的图像； （2）求不等式 ( ) ( 1 )f x f x 的解集． 2020 年普通高等学校招生全国统一考试 文科数学试题参考答案(A 卷) 选择题答案 一、选择题 1．D 2．C 3．C 4．A 5．D 6．B 7．C 8．B 9．C 10．D 11．B 12．A 非选择题答案 二、填空题 13．1 14．5 15．y=2x 16．7 三、解答题 17．解：（1）由试加工产品等级的频数分布表知， 甲分厂加工出来的一件产品为 A 级品的概率的估计值为 40 0.4100  ； 乙分厂加工出来的一件产品为 A 级品的概率的估计值为 28 0.28100  . （2）由数据知甲分厂加工出来的 100 件产品利润的频数分布表为 利润 65 25 −5 −75 频数 40 20 20 20 因此甲分厂加工出来的 100 件产品的平均利润为 654025205207520 15100   . 由数据知乙分厂加工出来的 100 件产品利润的频数分布表为 利润 70 30 0 −70 频数 28 17 34 21 因此乙分厂加工出来的 100 件产品的平均利润为 70 28 30 17 0 34 70 21 10100    . 比较甲乙两分厂加工的产品的平均利润，应选甲分厂承接加工业务. 18．解：（1）由题设及余弦定理得 2 2 228 3 2 3 cos150c c c     ， 解得 2c  （舍去）， 2c  ，从而 23a  . ABC△ 的面积为 1 232sin15032  ． （2）在 中， 18030ABCC ，所以 sin3sinsin(30)3sinsin(30)ACCCC ， 故 2sin(30) 2C . 而 0 3 0 C    ，所以 3 0 4 5 C   ，故 15C . 19．解：（1）由题设可知，PA=PB= PC． 由于△ABC 是正三角形，故可得△PAC≌△PAB． △PAC≌△PBC． 又∠APC =90°，故∠APB=90°，∠BPC=90°． 从而 PB⊥PA，PB⊥PC，故 PB⊥平面 PAC，所以平面 PAB⊥平面 PAC． （2）设圆锥的底面半径为 r，母线长为 l． 由题设可得 rl= 3 ， 222lr． 解得 r=1，l= ， 从而 3AB  ．由（1）可得 222PAPBAB，故 6 2PAPBPC ． 所以三棱锥 P-ABC 的体积为 3111166 ()323228PAPBPC ． 20．解：（1）当a=1时，f（x）=ex–x–2，则 fx（ ）=ex–1． 当x<0时， <0；当x>0时， >0． 所以f（x）在（–∞，0）单调递减，在（0，+∞）单调递增． （2） =ex–a． 当a≤0时， fx（ ）>0，所以f（x）在（–∞，+∞）单调递增， 故f（x）至多存在1个零点，不合题意． 当a>0时，由 =0可得x=lna． 当x∈（–∞，lna）时， <0； 当x∈（lna，+∞）时， >0．所以f（x）在（–∞，lna）单调递减，在（lna，+∞）单调递增，故当 x=lna时，f（x）取得最小值，最小值为f（lna）=–a（1+lna）． （i）若0≤a≤ 1 e ，则f（lna）≥0，f（x）在（–∞，+∞）至多存在1个零点，不合题意． （ii）若a> ，则f（lna）<0． 由于f（–2）=e–2>0，所以f（x）在（–∞，lna）存在唯一零点． 由（1）知，当x>2时，ex–x–2>0，所以当x>4且x>2ln（2a）时， ln(2 )22()ee(2)e(2)(2)20 2 xx a xfxa xa xa ． 故f（x）在（lna，+∞）存在唯一零点，从而f（x）在（–∞，+∞）有两个零点． 综上，a的取值范围是（ 1 e ，+∞）． 21．解：（1）由题设得 (,0),(,0),(0,1)AaBaG ． 则 (,1)AGa ， (,1)GBa．由 8AGGB得 2 18a ，即 3a  ． 所以 E 的方程为 2 2 19 x y． （2）设 1122(,),(,),(6,)CxyD xyPt ． 若 0t  ，设直线 CD 的方程为 xmyn，由题意可知 33n ． 由于直线 PA 的方程为 (3)9 tyx，所以 11(3)9 tyx． 直线 PB 的方程为 (3)3 tyx，所以 22(3)3 tyx． 可得 12213(3)(3)y xyx ． 由于 2 22 2 19 x y，故 2 22 2 ( 3)( 3) 9 xxy  ，可得 1 2 1 227 ( 3)( 3)y y x x    ， 即 22 1 2 1 2(27 ) ( 3)( ) ( 3) 0m y y m n y y n       ．① 将 代入 得 2 2 2( 9) 2 9 0m y mny n     ． 所以 2 1212 22 29,99 mnnyyyy mm     ． 代入①式得 2222(27)(9)2(3)(3)(9)0mnm nmnnm ． 解得 3n  （舍去）， 3 2n  ． 故直线 CD 的方程为 3 2x my，即直线 过定点 3( ,0)2 ． 若 0t  ，则直线CD 的方程为 0y  ，过点 ． 综上，直线 过定点 ． 22．解：当 k=1 时， 1 c o s ,: s i n , xtC yt    消去参数 t 得 221xy，故曲线 1C 是圆心为坐标原点，半径为 1 的圆． （2）当 k=4 时， 4 1 4 cos ,: sin , xtC yt    消去参数 t 得 的直角坐标方程为 1xy． 2C 的直角坐标方程为 4 16 3 0xy   ． 由 1, 41630 xy xy    解得 1 4 1 4 x y     ． 故 与 的公共点的直角坐标为 11( , )44 ． 23．解：（1）由题设知 13,, 3 1()51,1, 3 3,1. xx fxxx xx        ()y f x 的图像如图所示． （2）函数 ()y f x 的图像向左平移 1 个单位长度后得到函数 ( 1 )y f x的图像． 的图像与 的图像的交点坐标为 7 1 1( , ) 66 ． 由图像可知当且仅当 7 6x  时， 的图像在 的图像上方， 故不等式 ( ) ( 1 )f x f x 的解集为 7( , ) 6   ．