2018版高考文科数学(北师大版)一轮文档讲义:章9-4直线与圆
第4讲 直线与圆、圆与圆的位置关系
最新考纲 1.能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系;2.能用直线和圆的方程解决一些简单的问题;3.初步了解用代数方法处理几何问题的思想.
知 识 梳 理
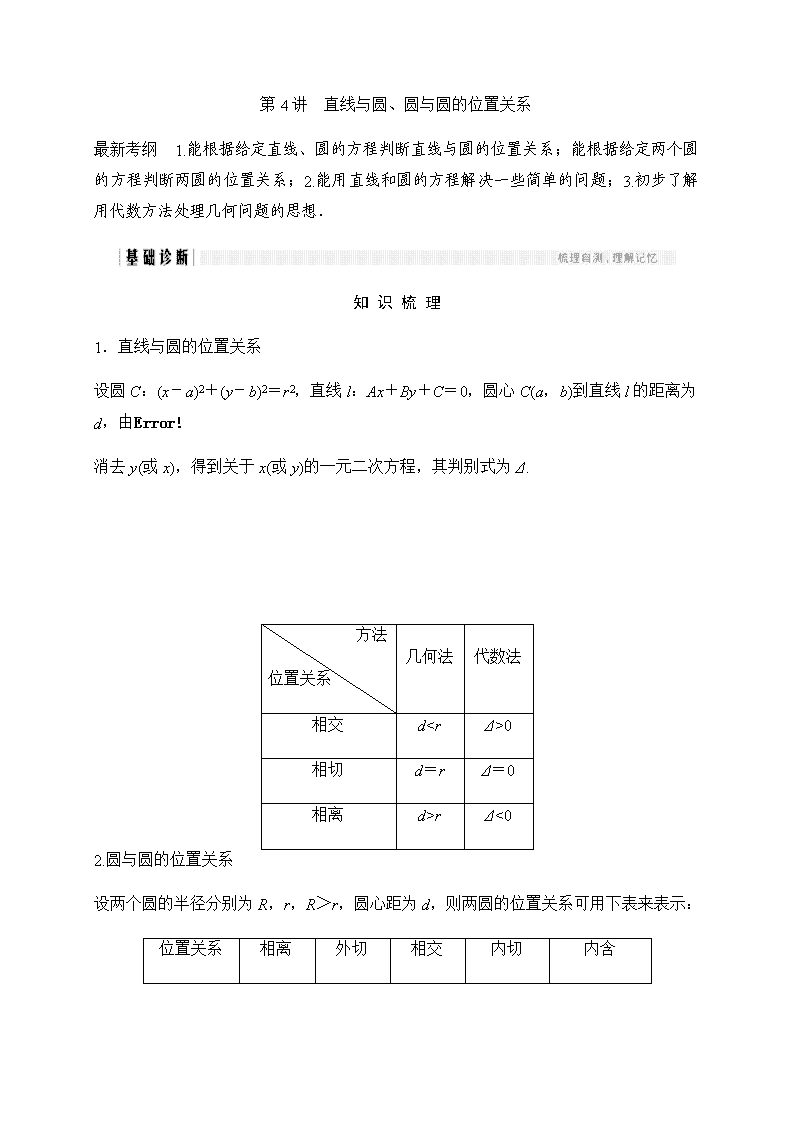
1.直线与圆的位置关系
设圆C:(x-a)2+(y-b)2=r2,直线l:Ax+By+C=0,圆心C(a,b)到直线l的距离为d,由
消去y(或x),得到关于x(或y)的一元二次方程,其判别式为Δ.
方法
位置关系
几何法
代数法
相交
d
0
相切
d=r
Δ=0
相离
d>r
Δ<0
2.圆与圆的位置关系
设两个圆的半径分别为R,r,R>r,圆心距为d,则两圆的位置关系可用下表来表示:
位置关系
相离
外切
相交
内切
内含
几何特征
d>R+r
d=R+r
R-r<d<R+r
d=R-r
d<R-r
代数特征
无实数解
一组实数解
两组实数解
一组实数解
无实数解
公切线条数
4
3
2
1
0
诊 断 自 测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)“k=1”是“直线x-y+k=0与圆x2+y2=1相交”的必要不充分条件.( )
(2)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.( )
(3)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )
(4)从两相交圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程.( )
(5)过圆O:x2+y2=r2上一点P(x0,y0)的圆的切线方程是x0x+y0y=r2.( )
解析 (1)“k=1”是“直线x-y+k=0与圆x2+y2=1相交”的充分不必要条件.
(2)除外切外,还有可能内切.
(3)两圆还可能内切或内含.
答案 (1)× (2)× (3)× (4)√ (5)√
2.(2015·安徽卷)直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b的值是( )
A.-2或12 B.2或-12
C.-2或-12 D.2或12
解析 圆的标准方程为(x-1)2+(y-1)2=1,圆心(1,1)到直线3x+4y=b的距离为=1,解得b=2或b=12,故选D.
答案 D
3.(2017·西安调研)若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )
A.[-3,-1] B.[-1,3]
C.[-3,1] D.(-∞,-3]∪[1,+∞)
解析 由题意可得,圆的圆心为(a,0),半径为,
∴≤,即|a+1|≤2,解得-3≤a≤1.
答案 C
4.(2015·湖南卷)若直线3x-4y+5=0与圆x2+y2=r2(r>0)相交于A,B两点,且∠AOB=120°(O为坐标原点),则r=________.
解析 如图,过O点作OD⊥AB于D点,在Rt△DOB中,∠DOB=60°,∴∠DBO=30°,
又|OD|==1,
∴r=2|OD|=2.
答案 2
5.(必修2P86B3改编)圆x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦长为________.
解析 由得x-y+2=0.又圆x2+y2=4的圆心到直线x-y+2=0的距离为=
.由勾股定理得弦长的一半为=,所以,所求弦长为2.
答案 2
考点一 直线与圆的位置关系
【例1】 (1)“a=3”是“直线y=x+4与圆(x-a)2+(y-3)2=8相切”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(2)直线y=-x+m与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
A.(,2) B.(,3)
C. D.
解析 (1)若直线y=x+4与圆(x-a)2+(y-3)2=8相切,则有=2,即|a+1|=4,所以a=3或-5.但当a=3时,直线y=x+4与圆(x-a)2+(y-3)2=8一定相切,故“a=3”是“直线y=x+4与圆(x-a)2+(y-3)2=8相切”的充分不必要条件.
(2)当直线经过点(0,1)时,直线与圆有两个不同的交点,此时m=1;当直线与圆相切时有圆心到直线的距离d==1,解得m=(切点在第一象限),所以要使直线与圆在第一象限内有两个不同的交点,则1<m<.
答案 (1)A (2)D
规律方法 判断直线与圆的位置关系的常见方法
(1)几何法:利用d与r的关系.
(2)代数法:联立方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.
上述方法中最常用的是几何法,点与圆的位置关系法适用于动直线问题.
【训练1】 (1)已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交 C.相离 D.不确定
(2)(2017·大连双基测试)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是________.
解析 (1)因为M(a,b)在圆O:x2+y2=1外,所以a2+b2>1,而圆心O到直线ax+by=1的距离d==<1,故直线与圆O相交.
(2)法一 将直线方程代入圆方程,得(k2+1)x2+4kx+3=0,直线与圆没有公共点的充要条件是Δ=16k2-12(k2+1)<0,解得-<k<.
法二 圆心(0,0)到直线y=kx+2的距离d=,直线与圆没有公共点的充要条件是d>1,
即>1,解得-<k<.
答案 (1)B (2)-<k<
考点二 圆的切线、弦长问题
【例2】 (1)(2016·全国Ⅰ卷)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=2,则圆C的面积为________.
(2)过原点O作圆x2+y2-6x-8y+20=0的两条切线,设切点分别为P,Q,则线段PQ的长为________.
解析 (1)圆C:x2+y2-2ay-2=0,即C:x2+(y-a)2=a2+2,圆心为C(0,a),C到直线y=x+2a的距离为d==.又由|AB|=2,得2+2=a2+2,解得a2=2,所以圆的面积为π(a2+2)=4π.
(2)将圆的方程化为标准方程为(x-3)2+(y-4)2=5,则圆心为(3,4),半径长为.
由题意可设切线的方程为y=kx,则圆心(3,4)到直线y=kx的距离等于半径长,即=,解得k=或k=,则切线的方程为y=x或y=x.联立切线方程与圆的方程,解得两切点坐标分别为(4,2),,此即为P,Q的坐标,由两点间的距离公式得|PQ|=4.
答案 (1)4π (2)4
规律方法 (1)弦长的两种求法
①代数方法:将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系,根据弦长公式求弦长.
②几何方法:若弦心距为d,圆的半径长为r,则弦长l=2.
(2)圆的切线方程的两种求法
①代数法:设切线方程为y-y0=k(x-x0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0进而求得k.
②几何法:设切线方程为y-y0=k(x-x0),利用点到直线的距离公式表示出圆心到切线的距离d,然后令d=r,进而求出k.
【训练2】 (1)过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短弦的长为________.
(2)过点P(2,4)引圆(x-1)2+(y-1)2=1的切线,则切线方程为________.
解析 (1)设P(3,1),圆心C(2,2),则|PC|=,半径r=2,由题意知最短的弦过P(3,1)且与PC垂直,所以最短弦长为2=2.
(2)当直线的斜率不存在时,直线方程为x=2,此时,圆心到直线的距离等于半径,直线与圆相切,符合题意;当直线的斜率存在时,设直线方程为y-4=k(x-2),即kx-y+4-2k=0,∵直线与圆相切,∴圆心到直线的距离等于半径,即d===1,
解得k=,
∴所求切线方程为x-y+4-2×=0,
即4x-3y+4=0.
综上,切线方程为x=2或4x-3y+4=0.
答案 (1)2 (2)x=2或4x-3y+4=0
考点三 圆与圆的位置关系
【例3】 (2017·郑州调研)已知两圆x2+y2-2x-6y-1=0,x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
解 因为两圆的标准方程分别为(x-1)2+(y-3)2=11,
(x-5)2+(y-6)2=61-m,
所以两圆的圆心分别为(1,3),(5,6),半径分别为,,
(1)当两圆外切时,由=+,得m=25+10.
(2)当两圆内切时,因为定圆半径小于两圆圆心之间的距离5,所以-=5,解得m=25-10.
(3)由(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,得两圆的公共弦所在直线的方程为4x+3y-23=0.
故两圆的公共弦的长为2=2.
规律方法 (1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.
【训练3】 (1)(2016·山东卷)已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是( )
A.内切 B.相交
C.外切 D.相离
(2)(2017·合肥模拟)已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1 相外切,则ab的最大值为( )
A. B. C. D.2
解析 (1)∵圆M:x2+(y-a)2=a2,∴圆心坐标为M(0,a),半径r1为a,圆心M到直线x+y=0的距离d=,由几何知识得2+()2=a2,解得a=2.∴M(0,2),r1=2.又圆N的圆心坐标N(1,1),半径r2=1,∴|MN|==,r1+r2=3,r1-r2=1.∴r1-r2<|MN|<r1+r2,∴两圆相交,故选B.
(2)由圆C1与圆C2相外切,可得=2+1=3,即(a+b)2=9,
根据基本不等式可知ab≤2=,
当且仅当a=b时等号成立.
答案 (1)B (2)C
[思想方法]
1.解决有关弦长问题的两种方法:
(1)几何法,直线被圆截得的半弦长,弦心距d和圆的半径r构成直角三角形,即r2=2+d2;
(2)代数法,联立直线方程和圆的方程,消元转化为关于x的一元二次方程,由根与系数的关系即可求得弦长|AB|=|x1-x2|=或|AB|=|y1-y2|=.
2.求过一点的圆的切线方程时,首先要判断此点是否在圆上,然后设出切线方程.注意:斜率不存在的情形.
[易错防范]
1.求圆的弦长问题,注意应用圆的性质解题,即用圆心与弦中点连线与弦垂直的性质,可以用勾股定理或斜率之积为-1列方程来简化运算.
2.过圆上一点作圆的切线有且只有一条;过圆外一点作圆的切线有且只有两条,若仅求得一条,除了考虑运算过程是否正确外,还要考虑斜率不存在的情况,以防漏解.
基础巩固题组
(建议用时:40分钟)
一、选择题
1.(2016·全国Ⅱ卷)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( )
A.- B.- C. D.2
解析 由圆的方程x2+y2-2x-8y+13=0得圆心坐标为(1,4),由点到直线的距离公式得d==1,解之得a=-.
答案 A
2.(2017·景德镇模拟)过点(3,1)作圆(x-1)2+y2=r2的切线有且只有一条,则该切线的方程为( )
A.2x+y-5=0 B.2x+y-7=0
C.x-2y-5=0 D.x-2y-7=0
解析 ∵过点(3,1)作圆(x-1)2+y2=r2的切线有且只有一条,∴点(3,1)在圆(x-1)2+y2=r2上,
∵圆心与切点连线的斜率k==,
∴切线的斜率为-2,
则圆的切线方程为y-1=-2(x-3),即2x+y-7=0.故选B.
答案 B
3.已知圆x2+y2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是( )
A.-2 B.-4 C.-6 D.-8
解析 将圆的方程化为标准方程为(x+1)2+(y-1)2=2-a,所以圆心为(-1,1),半径r=,圆心到直线x+y+2=0的距离d==,故r2-d2=4,即2-a-2=4,所以a=-4,故选B.
答案 B
4.圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为的点共有( )
A.1个 B.2个 C.3个 D.4个
解析 圆的方程化为(x+1)2+(y+2)2=8,圆心(-1,-2)到直线距离d==,半径是2,结合图形可知有3个符合条件的点.
答案 C
5.(2017·福州模拟)过点P(1,-2)作圆C:(x-1)2+y2=1的两条切线,切点分别为A,B,则AB所在直线的方程为( )
A.y=- B.y=- C.y=- D.y=-
解析 圆(x-1)2+y2=1的圆心为(1,0),半径为1,以|PC|==2为直径的圆的方程为(x-1)2+(y+1)2=1,
将两圆的方程相减得AB所在直线的方程为2y+1=0,即y=-. 故选B.
答案 B
二、填空题
6.(2016·全国Ⅲ卷) 已知直线l:x-y+6=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=________.
解析 设A(x1,y1),B(x2,y2),由
得y2-3y+6=0,解得y1=,y2=2,
∴A(-3,),B(0,2).
过A,B作l的垂线方程分别为
y-=-(x+3),y-2=-x,令y=0,
得xC=-2,xD=2,∴|CD|=2-(-2)=4.
答案 4
7.(2017·兰州月考)点P在圆C1:x2+y2-8x-4y+11=0上,点Q在圆C2:x2+y2+4x+2y+1=0上,则|PQ|的最小值是________.
解析 把圆C1、圆C2的方程都化成标准形式,得
(x-4)2+(y-2)2=9,(x+2)2+(y+1)2=4.
圆C1的圆心坐标是(4,2),半径长是3;圆C2的圆心坐标是(-2,-1),半径是2.
圆心距d==3.
所以,|PQ|的最小值是3-5.
答案 3-5
8.(2017·铜川一模)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为________.
解析 设直线上一点为P,切点为Q,圆心为M,则|PQ|即切线长,MQ为圆M的半径,长度为1,|PQ|==.
要使|PQ|最小,即求|PM|的最小值,此题转化为求直线y=x+1上的点到圆心M的最小距离.
设圆心到直线y=x+1的距离为d,则d==2.所以|PM|的最小值为2.所以|PQ|=≥=.
答案
三、解答题
9.(2015·全国Ⅰ卷)已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若·=12,其中O为坐标原点,求|MN|.
解 (1)易知圆心坐标为(2,3),半径r=1,
由题设,可知直线l的方程为y=kx+1,
因为l与C交于两点,所以<1.
解得0,
所以不论k为何实数,直线l和圆C总有两个交点.
(2)解 设直线与圆交于A(x1,y1),B(x2,y2)两点,
则直线l被圆C截得的弦长|AB|=|x1-x2|
=2=2 ,
令t=,则tk2-4k+(t-3)=0,
当t=0时,k=-,当t≠0时,因为k∈R,
所以Δ=16-4t(t-3)≥0,
解得-1≤t≤4,且t≠0,
故t=的最大值为4,此时|AB|最小为2.
法二 (1)证明 因为不论k为何实数,直线l总过点P(0,1),而|PC|=<2=R,所以点P(0,1)在圆C的内部,即不论k为何实数,直线l总经过圆C内部的定点P.所以不论k为何实数,直线l和圆C总有两个交点.
(2)解 由平面几何知识知过圆内定点P(0,1)的弦,只有与PC(C为圆心)垂直时才最短,而此时点P(0,1)为弦AB的中点,由勾股定理,知|AB|=2=2,即直线l被圆C截得的最短弦长为2.
能力提升题组
(建议用时:20分钟)
11.(2017·衡水中学月考)两圆x2+y2+2ax+a2-4=0 和x2+y2-4by-1+4b2=0恰有三条公切线,若a∈R,b∈R且ab≠0,则+的最小值为( )
A.1 B.3 C. D.
解析 x2+y2+2ax+a2-4=0,即(x+a)2+y2=4,x2+y2-4by-1+4b2=0,即x2+(y-2b)2=1.依题意可得,两圆外切,则两圆圆心距离等于两圆的半径之和,
则=1+2=3,即a2+4b2=9,
所以+==≥=1,当且仅当=,即a=±b时取等号.
答案 A
12.(2015·山东卷)一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为( )
A.-或- B.-或-
C.-或- D.-或-
解析 由已知,得点(-2,-3)关于y轴的对称点为(2,-3),由入射光线与反射光线的对称性,知反射光线一定过点(2,-3).设反射光线所在直线的斜率为k,则反射光线所在直线的方程为y+3=k(x-2),即kx-y-2k-3=0.由反射光线与圆相切,则有d==1,解得k=-或k=-,故选D.
答案 D
13.已知曲线C:x=-,直线l:x=6,若对于点A(m,0),存在C上的点P和l上的点Q使得+=0,则m的取值范围为________.
解析 曲线C:x=-,是以原点为圆心,2为半径的半圆,并且xP∈[-2,0],对于点A(m,0),存在C上的点P和l上的点Q使得+=0,
说明A是PQ的中点,Q的横坐标x=6,
∴m=∈[2,3].
答案 [2,3]
14.(2017·湖南省东部六校联考)已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
解 (1)设圆心C(a,0),则=2⇒a=0或a=-5(舍).
所以圆C的方程为x2+y2=4.
(2)当直线AB⊥x轴时,x轴平分∠ANB.
当直线AB的斜率存在时,设直线AB的方程为y=k(x-1),N(t,0),A(x1,y1),B(x2,y2),
由得(k2+1)x2-2k2x+k2-4=0,
所以x1+x2=,x1x2=.
若x轴平分∠ANB,则kAN=-kBN⇒+=0⇒+=0⇒2x1x2-(t+1)(x1+x2)+2t=0⇒-+2t=0⇒t=4,所以当点N为(4,0)时,能使得∠ANM=∠
BNM总成立.
特别提醒:教师配赠习题、课件、视频、图片、文档等各种电子资源见《创新设计·高考总复习》光盘中内容.