高一数学必修2高考真题集训1

高一数学必修2高考真题集训1

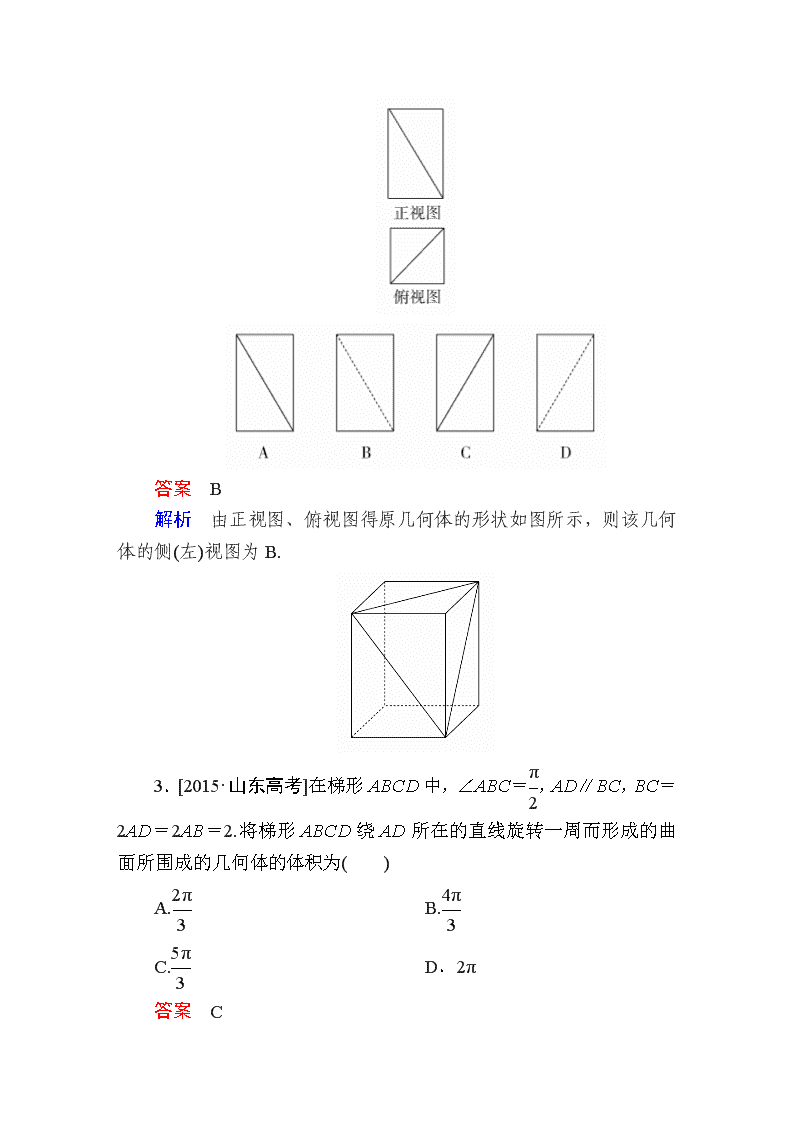
第一章　高考真题集训 一、选择题 ‎1．[2016·全国卷Ⅱ]如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为(　　)‎ A．20π B．24π C．28π D．32π 答案　C 解析　该几何体的表面积由圆锥的侧面积、圆柱的侧面积和圆柱的一个底面圆的面积组成．其中，圆锥的底面半径为2，母线长为＝4，圆柱的底面半径为2，高为4，故所求表面积S＝π×2×4＋2π×2×4＋π×22＝28π.‎ ‎2．[2016·天津高考] 将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧(左)视图为(　　)‎ 答案　B 解析　由正视图、俯视图得原几何体的形状如图所示，则该几何体的侧(左)视图为B.‎ ‎3．[2015·山东高考]在梯形ABCD中，∠ABC＝，AD∥BC，BC＝2AD＝2AB＝2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为(　　)‎ A. B. C. D．2π 答案　C 解析　如图，过点D作BC的垂线，垂足为H.则由旋转体的定义可知，该梯形绕AD所在的直线旋转一周而形成的曲面所围成的几何体为一个圆柱挖去一个圆锥．其中圆柱的底面半径R＝AB＝1，高h1＝BC＝2，其体积V1＝πR2h1＝π×12×2＝2π；圆锥的底面半径r＝DH＝1，高h2＝1，其体积V2＝πr2h2＝π×12×1＝.‎ 故所求几何体的体积为V＝V1－V2＝2π－＝.故选C.‎ ‎4．[2015·全国卷Ⅰ] 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(　　)‎ A．14斛 B．22斛 C．36斛 D．66斛 答案　B 解析　由l＝×2πr＝8得圆锥底面的半径r＝≈，所以米堆的体积V＝×πr2h＝××5＝，所以堆放的米有÷1.62≈22斛，故选B.‎ ‎5．[2016·山东高考]一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为(　　)‎ A.＋π B.＋π C.＋π D．1＋π 答案　C 解析　根据三视图可知，四棱锥的底面是边长为1的正方形、高是1，半球的半径为，所以该几何体的体积为×1×1×1＋×π3＝＋π.‎ ‎6．[2015·陕西高考]一个几何体的三视图如图所示，则该几何体的表面积为(　　)‎ A．3π B．4π C．2π＋4 D．3π＋4‎ 答案　D 解析　由所给三视图可知，该几何体是圆柱从底面圆直径处垂直切了一半，故该几何体的表面积为×2π×1×2＋2××π×12＋2×2＝3π＋4，故选D.‎ ‎7．[2016·全国卷Ⅲ]如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为(　　)‎ A．18＋36 B．54＋18 C．90 D．81‎ 答案　B 解析　由三视图，知该几何体是一个斜四棱柱，所以该几何体的表面积S＝2×3×6＋2×3×3＋2×3×3＝54＋18，故选B.‎ ‎8．[2015·安徽高考]一个四面体的三视图如图所示，则该四面体的表面积是(　　)‎ A．1＋ B．1＋2 C．2＋ D．2 答案　C 解析　在长、宽、高分别为2、1、1的长方体中，该四面体是如图所示的三棱锥P－ABC，表面积为SP－ABC＝2S△PAC＋2S△PBC＝×1×2×2＋×()2×2＝2＋.‎ ‎9. [2015·全国卷Ⅰ]圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r＝(　　)‎ A．1‎ B．2‎ C．4‎ D．8‎ 答案　B 解析　由三视图可知，此几何体是由半个圆柱与半个球组合而成的，其表面积为πr2＋2πr2＋4r2＋2πr2＝20π＋16，所以r＝2，故选B.‎ ‎10．[2015·全国卷Ⅱ]已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O－ABC体积的最大值为36，则球O的表面积为(　　)‎ A．36π B．64π C．144π D．256π 答案　C 解析　如图，设点C到平面OAB的距离为h，球O的半径为R ‎，因为∠AOB＝90°，所以S△OAB＝R2，要使VO－ABC＝·S△OAB·h最大，则OA，OB，OC应两两垂直，且(VO－ABC)max＝×R2×R＝R3＝36，此时R＝6，所以球O的表面积为S球＝4πR2＝144π.故选C.‎ ‎11．[2015·全国卷Ⅱ]一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为(　　)‎ A. B. C. D. 答案　D 解析　如图，不妨设正方体的棱长为1，则截去部分为三棱锥A－A1B1D1，其体积为，又正方体的体积为1，则剩余部分的体积为，故所求比值为.故选D.‎ ‎12．[2014·四川高考]某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是(　　)‎ A．3 B．2‎ C. D．1‎ 答案　D 解析　由俯视图可知三棱锥的底面是一个边长为2的正三角形，底面面积为×2×2×sin60°＝，由侧视图可知三棱锥的高为，故此三棱锥的体积V＝××＝1，故选D.‎ 二、填空题 ‎13．[2015·江苏高考]现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．‎ 答案　 解析　底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱的总体积为π×52×4＋π×22×8＝.设新的圆锥和圆柱的底面半径为r，则π×r2×4＋π×r2×8＝r2＝，解得r＝.‎ ‎14．[2016·四川高考]已知某三棱锥的三视图如图所示，则该三棱锥的体积是________．‎ 答案　 解析　根据三视图可知该三棱锥的底面积S＝×2×1＝，高为1，所以该三棱锥的体积V＝××1＝.‎ ‎15．[2014·山东高考]三棱锥P－ABC中，D，E分别为PB，PC的中点，记三棱锥D－ABE的体积为V1，P－ABC的体积为V2，则＝________.‎ 答案　 解析　如图，设点C到平面PAB的距离为h，△PAB的面积为S，则V2＝Sh，V1＝VE－ADB＝×S×h＝Sh，所以＝.‎ ‎16．[2016·天津高考]已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示(单位：m)，则该四棱锥的体积为________m3.‎ 答案　2‎ 解析　根据三视图可知该四棱锥的底面是底边长为‎2 m、高为‎1 m的平行四边形，四棱锥的高为‎3 m，故其体积为×2×1×3＝2(m3)．‎