2017年度高考数学(文)二模试题(北京市海淀区)
北京海淀区
2014届高三第二学期期末练习
数学(文)试题
本试卷共150分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考
试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知全集为R,集合A={x|x≥1},那么集合等于
A.{x|x>l} B.{x| x> -1} C.{x| x
0)的准线经过双曲线x2一y2 =1的左顶点,则p=____.
11.执行如图所示的程序框图,则输出S的值为 .
12.下列函数中:
①y= -sin2x;②y=cos2x;③y=3sin(2x十),
其图象仅通过向左(或向右)平移就能与函数的图象重合
的是 。(填上符合要求的函数对应的序号)
13.已知实数a>0且a≠1,函数
若数列{an}满足,且{an}是等差数列,则
a= , b= 。
14.农业技术员进行某种作物的种植密度试验,把一块试验田划分为8块面积相
等的区域(除了种植密度,其它影响作物生长的因素都保持一致),种植密度
和单株产量统计如下:
根据上表所提供信息,第 号区域的总产量最大,该区域种植密度为____ 株/m2.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15.(本小题满分1 3分)
已知函数.
(I)求函数的最小正周期;
(Ⅱ)若函数有零点,求实数a的取值范围.
16.(本小题满分13分)
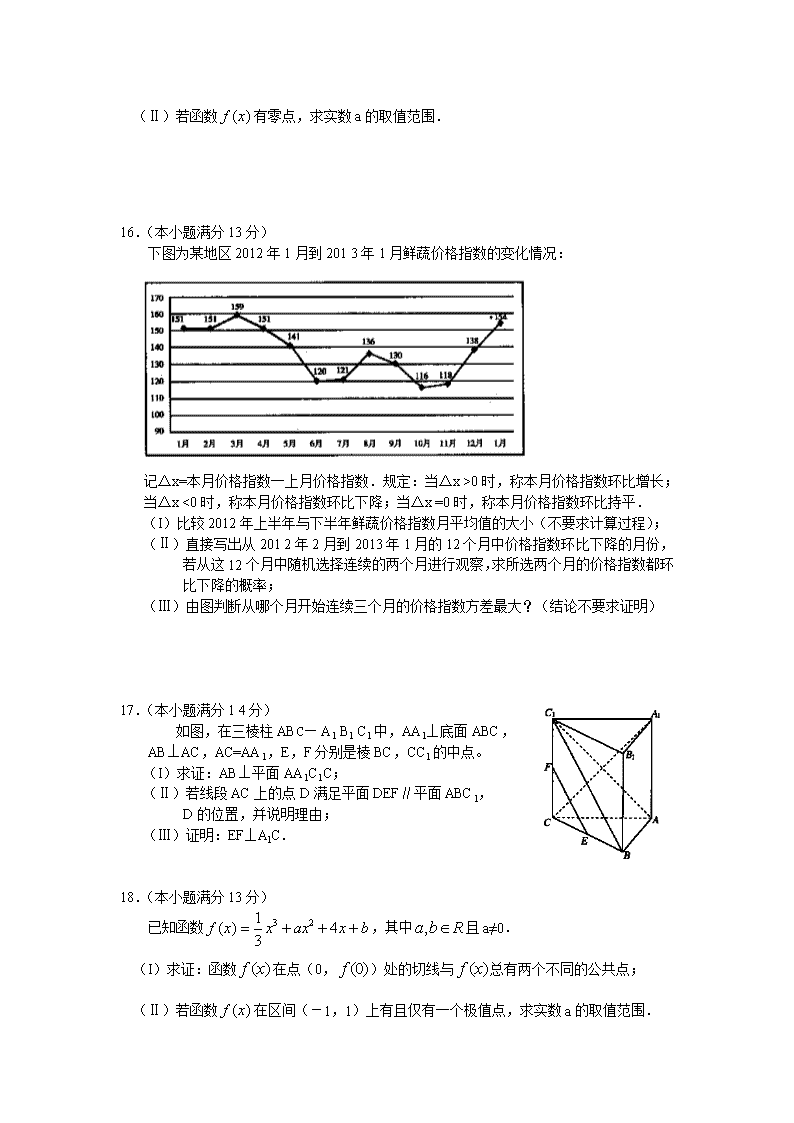
下图为某地区2012年1月到201 3年1月鲜蔬价格指数的变化情况:
记△x=本月价格指数一上月价格指数.规定:当△x >0时,称本月价格指数环比增长;
当△x <0时,称本月价格指数环比下降;当△x =0时,称本月价格指数环比持平.
(I)比较2012年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程);
(Ⅱ)直接写出从201 2年2月到2013年1月的12个月中价格指数环比下降的月份,若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数都环比下降的概率;
(Ⅲ)由图判断从哪个月开始连续三个月的价格指数方差最大?(结论不要求证明)
17.(本小题满分1 4分)
如图,在三棱柱ABC— A1 B1 C1中,AA1⊥底面ABC,
AB⊥AC,AC=AA1,E,F分别是棱BC,CC1的中点。
(I)求证:AB⊥平面AA1C1C;
(Ⅱ)若线段AC上的点D满足平面DEF∥平面ABC1,
D的位置,并说明理由;
(Ⅲ)证明:EF⊥AlC.
18.(本小题满分13分)
已知函数,其中且a≠0.
(I)求证:函数在点(0,)处的切线与总有两个不同的公共点;
(Ⅱ)若函数在区间(-1,1)上有且仅有一个极值点,求实数a的取值范围.
19.(本小题满分14分)
已知椭圆G的离心率为,其短轴两端点为A(0.1),B(0,一1).
(I)求椭圆G的方程;
(Ⅱ)若C,D是椭圆G上关于y轴对称的两个不同点,直线BC与x轴交于点M,判断以MD为直径的圆是否过点A,并说明理由.
20.(本小题满分1 3分)
给定正整数k≥3,若项数为k的数列{an}满足:对任意的i=1,2,…,k,均有(其中Sk=a1+a2+…+ak),则称数列{an}为“T数列”.
(I)判断数列一1,3,5,2,4和是否是“T教列”,并说明理由;
(Ⅱ)若{an}为“r数列”,求证:对i=1,2,…,k恒成立;
(Ⅲ)设{bn}是公差为d的无穷项等差数列,若对任意的正整数m≥3,b1,b2,…,bm均构成“T数列”,求{bn}的公差d.