- 2021-05-14 发布 |
- 37.5 KB |
- 4页


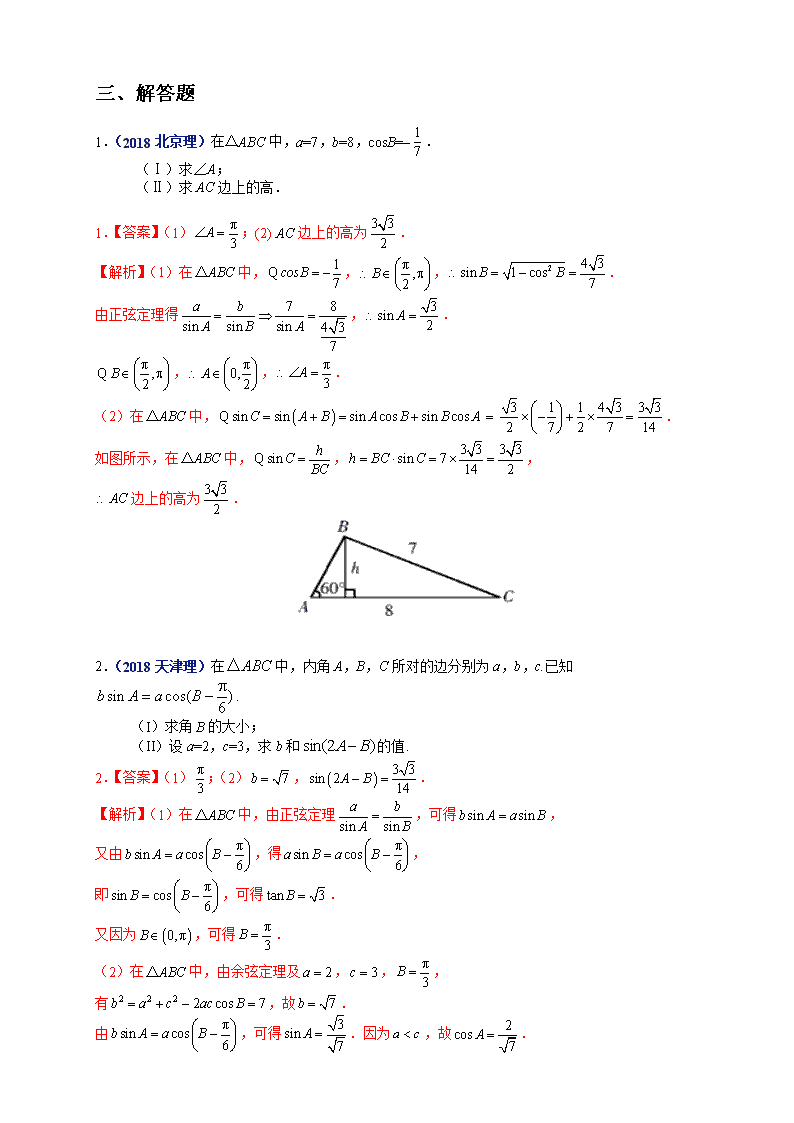
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全国各地高考数学试题及解答分类汇编大全09解三角形
2018年全国各地高考数学试题及解答分类汇编大全 (09解三角形) 一、选择题 1.(2018全国新课标Ⅰ理)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则( ) A.p1=p2 B.p1=p3 C.p2=p3 D.p1=p2+p3 1. 答案:A 解答:取,则, ∴区域Ⅰ的面积为,区域Ⅲ的面积为, 区域Ⅱ的面积为,故. 2.(2018全国新课标Ⅱ文、理)在中,,,,则( ) A. B. C. D. 2.【答案】A 【解析】因为, 所以,,选A. 3.(2018全国新课标Ⅲ文、理)的内角,,的对边分别为,,.若的面积为,则( ) A. B. C. D. 3.答案:C 解答:,又,故,∴.故选C. 二、填空 1.(2018北京文)若的面积为,且为钝角,则_________;的取值范围是_________. 1.【答案】;. 【解析】,, 即,,, 则, 为钝角,,,, 故. 2.(2018江苏)在中,角所对的边分别为,,的平分线交于点D,且,则的最小值为 ▲ . 2.【答案】9 【解析】由题意可知,,由角平分线性质和三角形面积公式得,化简得,,因此, 当且仅当时取等号,则的最小值为9. 3.(2018浙江)在△ABC中,角A,B,C所对的边分别为a,b,c.若a=,b=2,A=60°,则sin B=___________,c=___________. 3..答案: 解答:由正弦定理,得,所以. 由余弦定理,,得,所以. 4.(2018全国新课标Ⅰ文)△的内角的对边分别为,已知,,则△的面积为________. 4.答案: 解答:根据正弦定理有:,∴,∴.∵,∴,∴,∴. 三、解答题 1.(2018北京理)在△ABC中,a=7,b=8,cosB=–. (Ⅰ)求∠A; (Ⅱ)求AC边上的高. 1.【答案】(1);(2)边上的高为. 【解析】(1)在中,,,. 由正弦定理得,. ,,. (2)在中,. 如图所示,在中,,, 边上的高为. 2.(2018天津理)在中,内角A,B,C所对的边分别为a,b,c.已知. (I)求角B的大小; (II)设a=2,c=3,求b和的值. 2.【答案】(1);(2),. 【解析】(1)在中,由正弦定理,可得, 又由,得, 即,可得. 又因为,可得. (2)在中,由余弦定理及,,, 有,故. 由,可得.因为,故. 因此,, 所以,. 3.(2018全国新课标Ⅰ理)在平面四边形中,,,,. (1)求; (2)若,求. 3.答案:(1);(2)5. 解答: (1)在中,由正弦定理得:,∴, ∵,∴. (2),∴, ∴,∴, ∴.∴.查看更多