2019届高考数学一轮复习 第17讲 三角函数的图象和性质学案（无答案）文

2019届高考数学一轮复习 第17讲 三角函数的图象和性质学案（无答案）文

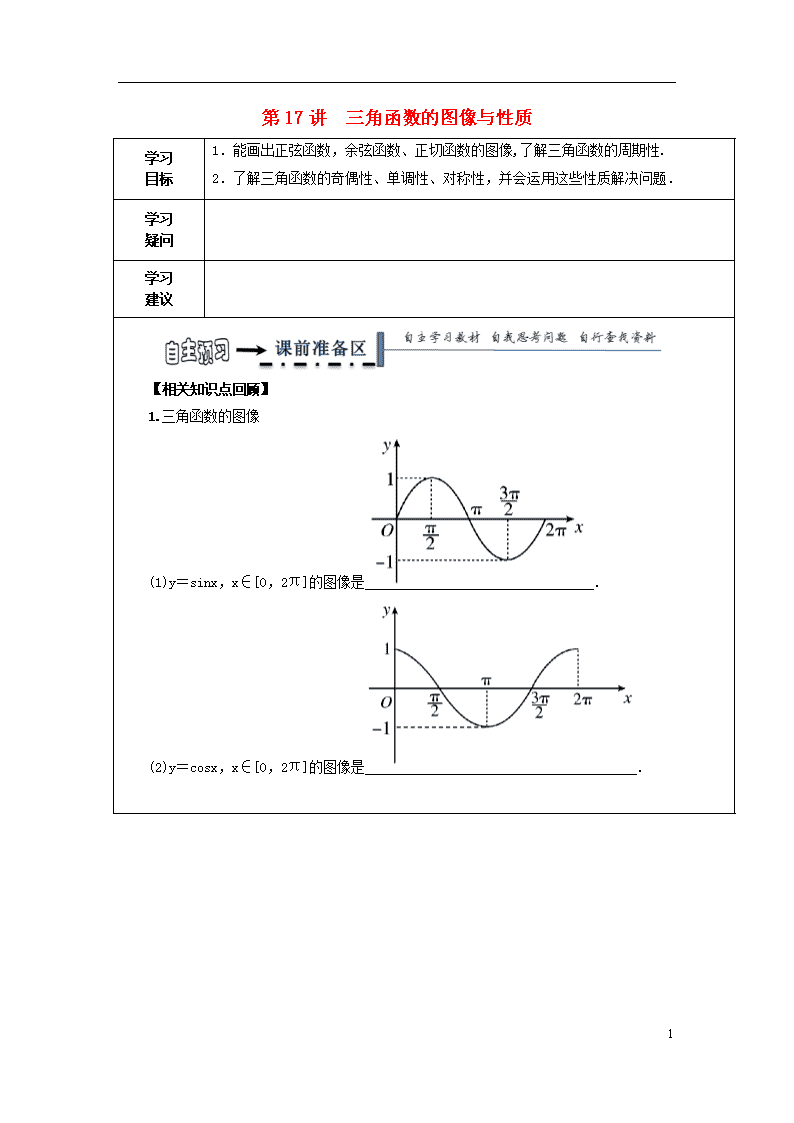
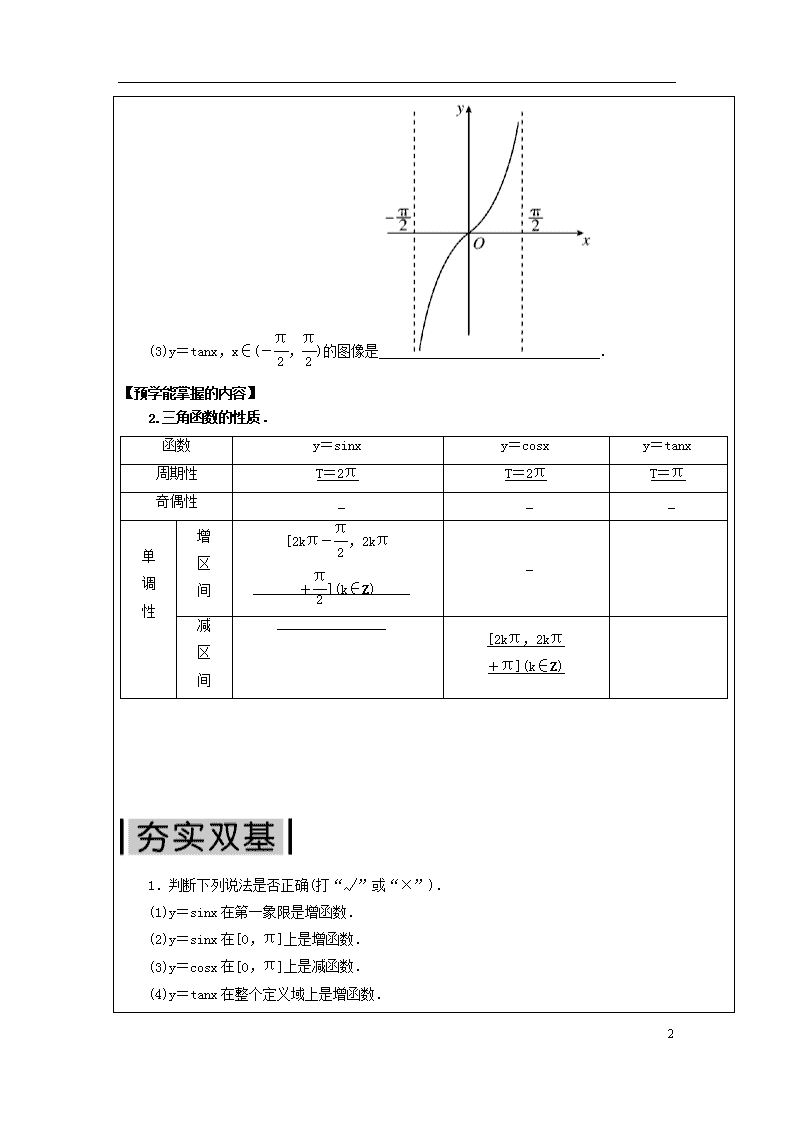
第17讲 三角函数的图像与性质 学习 目标 ‎1．能画出正弦函数，余弦函数、正切函数的图像,了解三角函数的周期性.‎ ‎2．了解三角函数的奇偶性、单调性、对称性，并会运用这些性质解决问题．‎ 学习 疑问 ‎ ‎ 学习 建议 ‎ ‎ ‎【相关知识点回顾】‎ ‎1.三角函数的图像 ‎(1)y＝sinx，x∈[0，2π]的图像是．‎ ‎(2)y＝cosx，x∈[0，2π]的图像是．‎ 5‎ ‎(3)y＝tanx，x∈(－，)的图像是．‎ ‎【预学能掌握的内容】‎ ‎2.三角函数的性质．‎ 函数 y＝sinx y＝cosx y＝tanx 周期性 T＝2π T＝2π T＝π 奇偶性 ‎ ‎ ‎ ‎ ‎ ‎ 单 调 性 增 区 间 ‎[2kπ－，2kπ ‎＋](k∈Z)‎ ‎ ‎ ‎ ‎ 减 区 间 ‎ ‎ ‎[2kπ，2kπ ‎＋π](k∈Z)‎ ‎ ‎ ‎ ‎ ‎1．判断下列说法是否正确(打“√”或“×”)．‎ ‎(1)y＝sinx在第一象限是增函数．‎ ‎(2)y＝sinx在[0，π]上是增函数．‎ ‎(3)y＝cosx在[0，π]上是减函数．‎ ‎(4)y＝tanx在整个定义域上是增函数．‎ 5‎ ‎(5)y＝sin(x＋)是奇函数．‎ ‎2．下列函数中，最小正周期为π的奇函数是(　　)‎ A．y＝sin(2x＋)　　　 B．y＝cos(2x＋)‎ C．y＝sin2x＋cos2x D．y＝sinx＋cosx ‎3．(1)函数y＝sin(x＋)的单调递增区间是________；‎ ‎(2)函数y＝tan(x－)的单调递增区间是________．‎ ‎ ‎ 5‎ ‎【探究点一】三角函数的周期性 ‎〖典例解析〗例1.求下列函数的周期：‎ ‎(1)y＝－sin(2x＋)＋6sinxcosx－2cos2x＋1；‎ ‎(2)y＝3|cos(2x－)|；‎ ‎(3)y＝|tanx|.‎ ‎〖概括小结〗求三角函数最小正周期的基本方法有两种：一是将所给函数化为y＝Asin(ωx＋φ)的形式；二是利用图像的根本特征，作出图像，观察得出．‎ y＝Asin(ωx＋φ)的最小正周期T＝.‎ y＝Atan(ωx＋φ)的最小正周期T＝.‎ ‎ 〖课堂检测〗(1)f(x)＝|sinx－cosx|的最小正周期为________．‎ ‎(2)若f(x)＝sinωx(ω>0)在[0，1]上至少存在50个最小值点，则ω的取值范围是________．‎ ‎【探究点二】三角函数的对称性 ‎〖典例解析〗例2.(1)求函数f(x)＝sin(2x－)的对称中心和对称轴方程．‎ ‎(2)设函数y＝sin2x＋acos2x的图像关于直线x＝－对称，求实数a的值．‎ ‎(3)求函数y＝tan(＋)的图像的对称中心．‎ ‎ ‎ ‎〖课堂检测〗(1)已知f(x)＝2sin(x＋)(x∈R)，函数y＝f(x＋φ)(|φ|≤)的图像关于直线x＝0对称，则φ的值为________．‎ ‎(2)函数y＝sin(2x＋)＋1的图像的一个对称中心的坐标是(　　)‎ A．(，0)　　　　　　 B．(，1)‎ 5‎ C．(，1) D．(－，－1)‎ ‎【探究点二】三角函数的单调性 ‎ ‎〖典例解析〗例3.求下列函数的单调区间．‎ ‎(1)y＝cos(－2x＋)的单调递减区间；‎ ‎(2)y＝3tan(－)的单调区间；‎ ‎(3)y＝－|sin(x＋)|的单调递减区间．‎ ‎〖课堂检测〗(1)y＝sin－cos的单调递增区间为________．‎ ‎(2)已知ω>0，函数f(x)＝sin(ωx＋)在(，π)上单调递减，则实数ω的取值范围是(　　)‎ A．[，]　　　　 B．[，]‎ C．(0，] D．(0，2]‎ 5‎ ‎【层次一】1．函数y＝cos(x＋)，x∈[0，]的值域是(　　)‎ A．(－，]　　　　　　 B．[－，]‎ C．[，] D．[－，－]‎ ‎2．如果|x|≤，那么函数f(x)＝cos2x＋sinx的最小值是(　　)‎ A. B．－ C．－1 D. ‎3．函数f(x)＝sin(2x－)在区间[0，]上的最小值为(　　)‎ A．－1 B．－ C. D．0‎ ‎ 【层次二】4.已知函数f(x)＝sin2x－sin2(x－)，x∈R.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)求f(x)在区间[－，]上的最大值和最小值．‎ ‎【思维导图】（学生自我绘制）‎ 5‎