- 2021-05-13 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
四川南充高三第一次高考适应性考试数学理
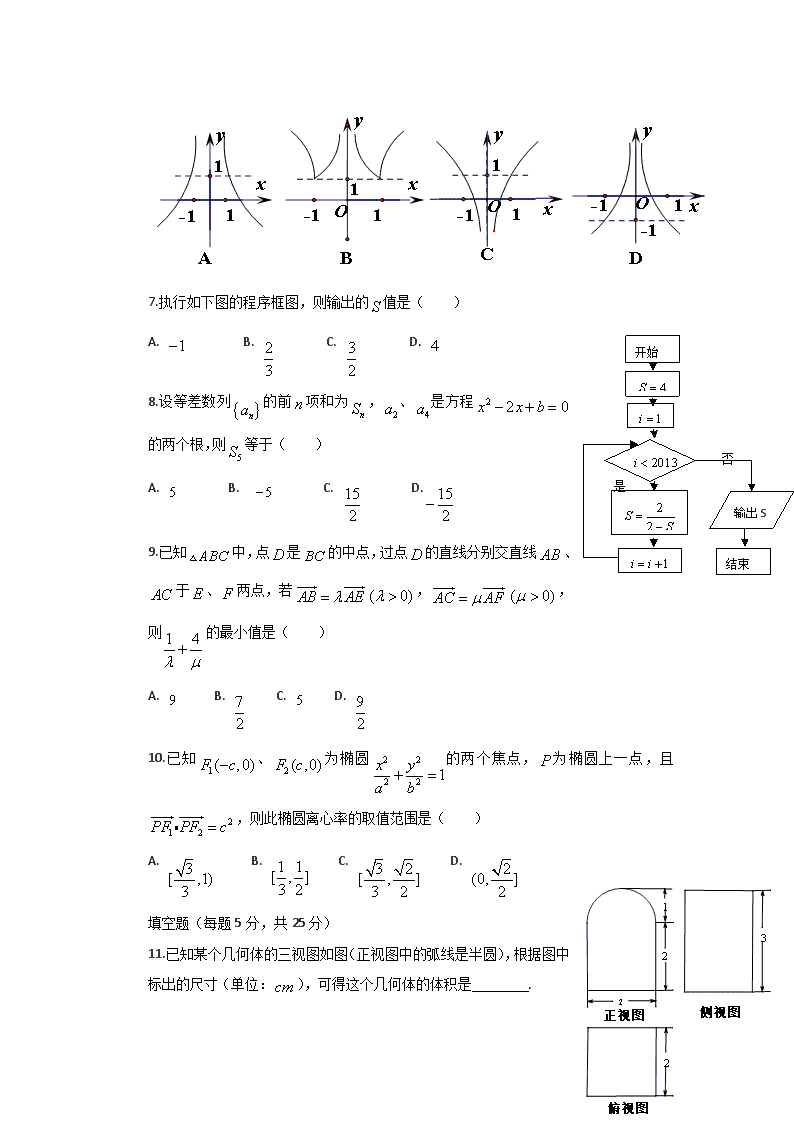
四川南充2019年高三第一次高考适应性考试-数学理 数学试卷(理科) (考试时间120分钟,满分150分) 一、 选择题(每题5分,共50分) 1.是虚数单位,复数=( ) A. B. C. D. 2.已知全集,集合,,则( ) A. B. C. D. 3.设是三条不同的直线,是两个不同的平面,则的一个充分条件是( ) A. B. C. D. A. B. C. D. 5.为了得到函数的图像,只需把函数的图像( ) A.向左平移个长度单位 B. 向右平移个长度单位 C. 向左平移个长度单位 D. 向右平移个长度单位 6.函数 的图像大致为下图的( ) 7.执行如下图的程序框图,则输出的值是( ) 开始 输出S 结束 是 否 A. B. C. D. 8.设等差数列的前项和为,、是方程的两个根,则等于( ) A. B. C. D. 9.已知中,点是的中点,过点的直线分别交直线、于、两点,若,,则的最小值是( ) A. B. C. D. 10.已知、为椭圆的两个焦点,为椭圆上一点,且,则此椭圆离心率的取值范围是( ) A. B. C. D. 填空题(每题5分,共25分) 11.已知某个几何体的三视图如图(正视图中的弧线是半圆),根据图中标出的尺寸(单位:),可得这个几何体的体积是 . 12.若的展开式中的系数是,则实数的值是 . 13.在体积为的三棱锥的棱上任取一点,则三棱锥的体积大于的概率是 . 14.已知是直线上的动点,、是圆的两条切线,、是切点,是圆心,那么四边形面积的最小值为 . 15.对于三次函数,定义是函数的导函数。若方程有实数解,则称点为函数的“拐点”。有同学发现:任何一个三次函数既有拐点,又有对称中心,且拐点就是对称中心。根据这一发现,对于函数,则…的值为 . 解答题(共6小题,共75分) 16.(此题满分12分) 已知的三个内角、、所对的边分别为、、;向量,,且. (I)求的大小; (II)若,求 17.(此题满分12分) 某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,现将初赛答卷成绩(得分均为整数,满分100分)进行统计,制成如下频率分布表: 分数(分数段) 频数(人数) 频率 ① 0.16 22 ② 14 0.28 ③ ④ 合计 50 1 (I)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案); (II)决赛规则如下:参加决赛的每位同学依次口答4道小题,只要答对2道题就终止答题,并获得一等奖,如果前三道题都答错,就不再答第四题。某同学进入决赛,每道题答对的概率的值恰好与频率分布表中不少于80分的频率的值相同. ①求该同学恰好答满4道题而获得一等奖的概率; ②记该同学决赛中答题个数为,求的分布列及数学期望. 18.(此题满分13分) 如图,是边长为3的正方形,平面,,,与平面所成的角. (I)求证:平面 (II)求二面角的余弦值; (III)设点是线段上一个动点,试确定的位置,使得平面,并证明你的结论. 19.(此题满分12分) 设数列的各项都为正数,其前项和为,已知对任意,是和的等差中项. (I)证明数列为等差数列,并求数列的通项公式; (II)证明. 20.(此题满分12分) 已知椭圆的中心在原点,焦点在轴上,一个顶点为,且其右焦点到直线的距离为3. (I)求椭圆的方程; (II)是否存在斜率为,且过定点的直线,使与椭圆交于两个不同的点、,且,若存在,求出直线的方程;若不存在,请说明理由 21.(此题满分14分) 设函数. (I)求函数的最小值; (II)设,讨论函数的单调性; (III)斜率为的直线与曲线交于、两点,求证:. 南充市高2018届第一次高考适应性考试 数学理科答案 一、 选择题(50分) 题 号 1 2 3 4 5 6 7 8 9 10 答 案 A D C A B C D A D C 二、 填空题(25分) 11. ; 12. 2 ; 13. ; 14. 2 ; 15. 3018 三、 解答题(75分) 16.(此题满分12分) 解:(Ⅰ) (Ⅱ) 17. (此题满分12分) 解:(Ⅰ) ① 8 ② 0.44 ③ 6 ④ 0.12 …………………………4分 (Ⅱ)由(Ⅰ)得:P = 0.4 ①该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道题.第4道也能够答对 才获得一等奖,则有 ……………………………6分 ②因为只要答对2道题就终止答题,并获得一等奖,所以该同学答题个数为2、3、4. 即X= 2、3、4 分布列为: ……………………………12分 18.(此题满分13分) 解:(Ⅰ证明:因为DE⊥平面ABCD, 所以DE⊥AC. 因为ABCD是正方形,所以AC⊥BD, 从而AC⊥平面BDE. ……………………………4分 (Ⅱ)因为DA,DC,DE两两垂直, 所以建立空间直角坐标系D-xyz如下图. 因为BE与平面ABCD所成角为60°, 即∠DBE=60°, 所以=. 因为正方形ABCD的边长为3,所以BD=3, 所以DE=3,AF=. 则A(3,0,0),F(3,0,),E(0,0,3),B(3,3,0),C(0,3,0), 所以=(0,-3,),=(3,0,-2), 设平面BEF的法向量为n=(x,y,z), 则即 令z=,则n=(4,2,). 因为AC⊥平面BDE,所以为平面BDE的一个法向量,=(3,-3,0), 所以cos〈n,〉===. 因为二面角为锐角,所以二面角F-BE-D的余弦值为. …………………9分 (Ⅲ)点M是线段BD上一个动点,设M(t,t,0). 则=(t-3,t,0), 因为AM∥平面BEF, 所以·n=0, 即4(t-3)+2t=0,解得t=2. 此时,点M坐标为(2,2,0),BM=BD,符合题意. …………………………13分 19.(此题满分12分) (Ⅱ)因为,则. ………10分 所以2(. …12分 20.(此题满分12分) 解:(Ⅰ)设椭圆的方程为,由已知得. 设右焦点为,由题意得 ……………………………2分 . 椭圆的方程为. ……………………4分 21.(此题满分14分) 解:(Ⅰ) (Ⅱ) (Ⅲ) 查看更多