新课标备战高考数学理专题强化复习十一章　算法初步

新课标备战高考数学理专题强化复习十一章　算法初步

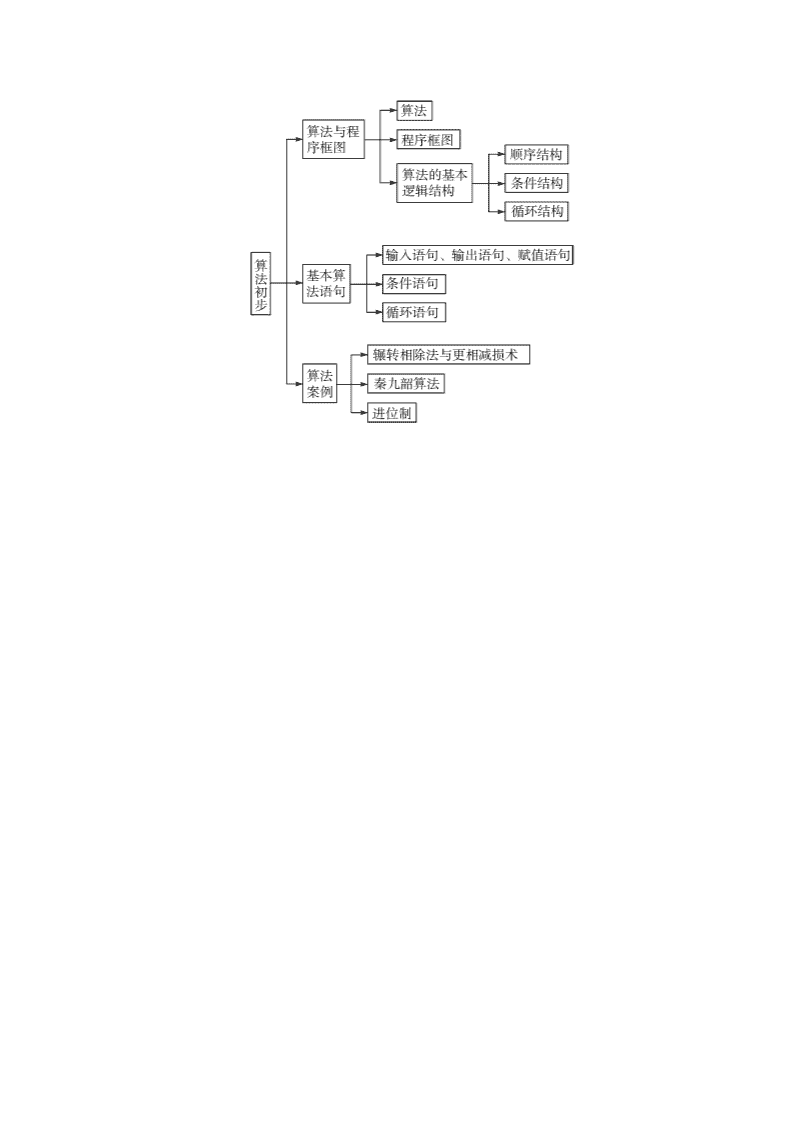
第十一章　算法初步 高考导航 考试要求 重难点击 命题展望 ‎　　1.了解算法的含义，了解算法的思想.‎ ‎2.理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构.‎ ‎3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.‎ ‎4.了解几个古代的算法案例，能用辗转相除法及更相减损术求最大公约数；用秦九韶算法求多项式的值；了解进位制，会进行不同进位制之间的转化.‎ ‎　　本章重点：1.算法的三种基本逻辑结构即顺序结构、条件结构和循环结构；2.输入语句、输出语句、赋值语句、条件语句、循环语句(两种形式)的结构、作用与功能及各种语句的格式要求.‎ 本章难点：1.用自然语言表示算法和运用程序框图表示算法；2.用算法的基本思想编写程序解决简单问题.弄清三种基本逻辑结构的区别，把握程序语言中所包含的一些基本语句结构.‎ ‎　　算法初步作为数学新增部分，在高考中一定会体现出它的重要性和实用性.‎ 高考中将重点考查对变量赋值的理解和掌握、对条件结构和循环结构的灵活运用，学会根据要求画出程序框图；预计高考中，将考查程序框图、循环结构和算法思想，并结合函数与数列考查逻辑思维能力.因此算法知识与其他知识的结合将是高考的重点，这也恰恰体现了算法的普遍性、工具性，当然难度不会太大，重在考查算法的概念及其思想.‎ ‎1.以选择题、填空题为主，重点考查算法的含义、程序框图、基本算法语句以及算法案例等内容.‎ ‎2.解答题中可要求学生设计一个计算的程序并画出程序框图，能很好地考查学生分析问题、解决问题的能力.‎ 知识网络 ‎11.1　算法的含义与程序框图 ‎　　　　　　　　　　　　　　　　　　‎ 典例精析 题型一　算法的含义 ‎【例1】已知球的表面积是16π，要求球的体积，写出解决该问题的一个算法.‎ ‎【解析】算法如下：‎ 第一步，s＝16π.‎ 第二步，计算R＝.‎ 第三步，计算V＝.‎ 第四步，输出V.‎ ‎【点拨】给出一个问题，设计算法应该注意：‎ ‎(1)认真分析问题，联系解决此问题的一般数学方法，此问题涉及到的各种情况；‎ ‎(2)将此问题分成若干个步骤；‎ ‎(3)用简练的语句将各步表述出来.‎ S＝1‎ I＝3‎ While I＜　①　‎ S＝S×I I＝I＋2‎ End While Print S End ‎【变式训练1】设计一个计算1×3×5×7×9×11×13的算法.图中给出程序的一部分，则在横线①上不能填入的数是(　　)‎ A.13‎ B.13.5‎ C.14‎ D.14.5‎ ‎【解析】当I＜13成立时，只能运算 ‎1×3×5×7×9×11.故选A.‎ 题型二　程序框图 ‎【例2】图一是某县参加2010年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10(如A2表示身高(单位：cm)在[150,155)内的学生人数).图二是统计图一中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160～180 cm(含‎160 cm，不含‎180 cm)的学生人数，那么在流程图中的判断框内应填写的条件是(　　)‎ A.i＜6？ B.i＜7？ C.i＜8？ D.i＜9？‎ 图一 ‎【解析】根据题意可知，i的初始值为4，输出结果应该是A4＋A5＋A6＋A7，因此判断框中应填写i＜8？，选C.‎ ‎【点拨】本题的命题角度较为新颖，信息量较大，以条形统计图为知识点进行铺垫，介绍了算法流程图中各个数据的引入来源，其考查点集中于循环结构的终止条件的判断，考查了学生合理地进行推理与迅速作出判断的解题能力，解本题的过程中不少考生误选A，实质上本题中的数据并不大，考生完全可以直接从头开始限次按流程图循环观察，依次写出每次循环后的变量的赋值，即可得解.‎ ‎【变式训练2】(2009辽宁)某店一个月的收入和支出，总共记录了N个数据a1，a2，…，aN.其中收入记为正数，支出记为负数，该店用如图所示的程序框图计算月总收入S和月净盈利V，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的(　　)‎ A.A＞0？，V＝S－T B.A＜0？，V＝S－T C.A＞0？，V＝S＋T D.A＜0？，V＝S＋T ‎【解析】选C.‎ 题型三　算法的条件结构 ‎【例3】某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：‎ f＝‎ 其中f(单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f的算法，并画出相应的程序框图.‎ ‎【解析】算法如下：‎ 第一步，输入物品重量ω.‎ 第二步，如果ω≤50，那么f＝0.53ω，‎ 否则，f＝50×0.53＋(ω－50)×0.85.‎ 第三步，输出托运费f.‎ 程序框图如图所示.‎ ‎【点拨】求分段函数值的算法应用到条件结构，因此在程序框图的画法中需要引入判断框，要根据题目的要求引入判断框的个数，而判断框内的条件不同，对应的框图中的内容或操作就相应地进行变化.‎ ‎【变式训练3】(2010天津)阅读如图的程序框图，若输出s的值为－7，则判断框内可填写(　　)‎ A.i＜3？‎ B.i＜4？‎ C.i＜5？‎ D.i＜6？‎ ‎【解析】i＝1，s＝2－1＝1；‎ i＝3，s＝1－3＝－2；‎ i＝5，s＝－2－5＝－7.所以选D.‎ 题型四　算法的循环结构 ‎【例4】设计一个计算10个数的平均数的算法，并画出程序框图.‎ ‎【解析】算法步骤如下：‎ 第一步，令S＝0.‎ 第二步，令I＝1.‎ 第三步，输入一个数G.‎ 第四步，令S＝S＋G.‎ 第五步，令I＝I＋1.‎ 第六步，若I＞10，转到第七步，‎ 若I≤10，转到第三步.‎ 第七步，令A＝S/10.‎ 第八步，输出A.‎ 据上述算法步骤，程序框图如图.‎ ‎【点拨】(1)引入变量S作为累加变量，引入I为计数变量，对于这种多个数据的处理问题，可通过循环结构来达到；(2)计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止，累加变量用于输出结果.‎ ‎【变式训练4】设计一个求1×2×3×…×10的程序框图.‎ ‎【解析】程序框图如下面的图一或图二.‎ ‎　　　‎ ‎　 图一　　　　　　　图二 总结提高 ‎1.给出一个问题，设计算法时应注意：‎ ‎(1)认真分析问题，联系解决此问题的一般数学方法；‎ ‎(2)综合考虑此类问题中可能涉及的各种情况；‎ ‎(3)借助有关的变量或参数对算法加以表述；‎ ‎(4)将解决问题的过程划分为若干个步骤；‎ ‎(5)用简练的语言将各个步骤表示出来.‎ ‎2.循环结构有两种形式，即当型和直到型，这两种形式的循环结构在执行流程上有所不同，当型循环是当条件满足时执行循环体，不满足时退出循环体；而直到型循环则是当条件不满足时执行循环体，满足时退出循环体.所以判断框内的条件，是由两种循环语句确定的，不得随便更改.‎ ‎3.条件结构主要用在一些需要依据条件进行判断的算法中.如分段函数的求值，数据的大小关系等问题的算法设计.‎ ‎11.2　基本算法语句 典例精析 题型一　输入、输出与赋值语句的应用 ‎【例1】阅读程序框图(如下图)，若输入m＝4，n＝6，则输出a＝　　　，i＝　　　.‎ ‎【解析】a＝12，i＝3.‎ ‎【点拨】赋值语句是一种重要的基本语句，也是程序必不可少的重要组成部分，使用赋值语句，要注意其格式要求.‎ ‎【变式训练1】(2010陕西)如图是求样本x1，x2，…，x10的平均数的程序框图，则图中空白框中应填入的内容为(　　)‎ A.S＝S＋xn B.S＝S＋ C.S＝S＋n D.S＝S＋ ‎【解析】因为此步为求和，显然为S＝S＋xn，故选A.‎ 题型二　循环语句的应用 ‎【例2】设计算法求＋＋＋…＋的值.要求画出程序框图，写出用基本语句编写的程序.‎ ‎【解析】这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示：‎ 程序如下：‎ s＝0‎ k＝1‎ DO ‎ s＝s＋1/(k* (k＋1))‎ ‎ k＝k＋1‎ LOOP UNTIL k＞99‎ PRINT s END ‎【点拨】(1)在用WHILE语句和UNTIL语句编写程序解决问题时，一定要注意格式和条件的表述方法，WHILE语句是当条件满足时执行循环体，UNTIL语句是当条件不满足时执行循环体.‎ ‎(2)在解决一些需要反复执行的运算任务，如累加求和、累乘求积等问题中应注意考虑利用循环语句来实现.‎ ‎(3)在循环语句中，也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套的这些语句，保证语句的完整性，否则就会造成程序无法执行.‎ ‎【变式训练2】下图是输出某个有限数列各项的程序框图，则该框图所输出的最后一个数据是　　　　.‎ ‎【解析】由程序框图可知，当N＝1时，A＝1；N＝2时，A＝；N＝3时，A＝，…，即输出各个A值的分母是以1为首项以2为公差的等差数列，故当N＝50时，A＝＝，即为框图最后输出的一个数据.故填.‎ 题型三　算法语句的实际应用 ‎【例3】‎ 某电信部门规定：拨打市内电话时，如果通话时间3分钟以内，收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计算).试设计一个计算通话费用的算法，要求写出算法，编写程序.‎ ‎【解析】我们用c(单位：元)表示通话费，t(单位：分钟)表示通话时间，‎ 则依题意有 算法步骤如下：‎ 第一步，输入通话时间t.‎ 第二步，如果t≤3，那么c＝0.2；否则c＝0.2＋0.1×[t－2].‎ 第三步，输出通话费用c.‎ 程序如下：‎ INPUT t IF t＜3　THEN c＝0.2‎ ELSE c＝0.2＋0.1*INT（t-2）‎ END IF PRINT c END ‎【点拨】在解决实际问题时，要正确理解其中的算法思想，根据题目写出其关系式，再写出相应的算法步骤，画出程序框图，最后准确地编写出程序，同时要注意结合题意加深对算法的理解.‎ ‎【变式训练3】(2010江苏)下图是一个算法流程图，则输出S的值是　　　　.‎ ‎【解析】n＝1时，S＝3；n＝2时，S＝3＋4＝7；n＝3时，S＝7＋8＝15；n＝4时，S＝15＋24＝31；n＝5时，S＝31＋25＝63.因为63≥33，所以输出的S值为63.‎ 总结提高 ‎1.输入、输出语句可以设计提示信息，加引号表示出来，与变量之间用分号隔开.‎ ‎2.赋值语句的赋值号左边只能是变量而不能是表达式；赋值号左右两边不能对换，不能利用赋值语句进行代数式计算，利用赋值语句可以实现两个变量值的互换，方法是引进第三个变量，用三个赋值语句完成.‎ ‎3.在某些算法中，根据需要，在条件语句的THEN分支或ELSE分支中又可以包含条件语句.遇到这样的问题，要分清内外条件结构，保证结构的完整性.‎ ‎4.分清WHILE语句和UNTIL语句的格式，在解决一些需要反复执行的运算任务，如累加求和，累乘求积等问题中应主要考虑利用循环语句来实现，但也要结合其他语句如条件语句.‎ ‎5.编程的一般步骤：‎ ‎(1)算法分析；(2)画出程序框图；(3)写出程序.‎ ‎11.3　算法案例 典例精析 题型一　求最大公约数 ‎【例1】(1)用辗转相除法求840与1 764的最大公约数；‎ ‎(2)用更相减损术求440与556的最大公约数.‎ ‎【解析】(1)用辗转相除法求840与1 764的最大公约数：‎ ‎1 764＝840×2＋84，‎ ‎840＝84×10＋0.‎ 所以840与1 764的最大公约数是84.‎ ‎(2)用更相减损术求440与556的最大公约数：‎ ‎556－440＝116，‎ ‎440－116＝324，‎ ‎324－116＝208，‎ ‎208－116＝92，‎ ‎ 116－92＝24，‎ ‎　92－24＝68，‎ ‎　68－24＝44，‎ ‎　44－24＝20，‎ ‎　24－20＝4，‎ ‎　20－4＝16，‎ ‎　16－4＝12，‎ ‎　12－4＝8，‎ ‎　　8－4＝4.‎ 所以440与556的最大公约数是4.‎ ‎【点拨】‎ ‎(1)辗转相除法与更相减损术是求两个正整数的最大公约数的方法，辗转相除法用较大的数除以较小的数，直到大数被小数除尽结束运算，较小的数就是最大公约数；更相减损术是用两数中较大的数减去较小的数，直到所得的差和较小数相等为止，这个较小数就是这两个数的最大公约数.一般情况下，辗转相除法步骤较少，而更相减损术步骤较多，但运算简易，解题时要灵活运用.‎ ‎(2)两个以上的数求最大公约数，先求其中两个数的最大公约数，再用所得的公约数与其他各数求最大公约数即可.‎ ‎【变式训练1】求147,343,133的最大公约数.‎ ‎【解析】先求147与343的最大公约数.‎ ‎343－147＝196，‎ ‎196－147＝49，‎ ‎ 147－49＝98，‎ ‎　98－49＝49，‎ 所以147与343的最大公约数为49.‎ 再求49与133的最大公约数.‎ ‎133－49＝84，‎ ‎ 84－49＝35，‎ ‎ 49－35＝14，‎ ‎ 35－14＝21，‎ ‎ 21－14＝7，‎ ‎　14－7＝7.‎ 所以147,343,133的最大公约数为7.‎ 题型二　秦九韶算法的应用 ‎【例2】用秦九韶算法写出求多项式f(x)＝1＋x＋0.5x2＋0.016 67x3＋0.041 67x4＋0.008 33x5在x＝－0.2时的值的过程.‎ ‎【解析】先把函数整理成f(x)＝((((0.008 33x＋0.041 67)x＋0.166 67)x＋0.5)x＋1)x＋1，‎ 按照从内向外的顺序依次进行.‎ x＝－0.2，‎ a5＝0.008 33， v0＝a5＝0.008 33；‎ a4＝0.041 67， v1＝v0x＋a4＝0.04；‎ a3＝0.016 67， v2＝v1x＋a3＝0.008 67；‎ a2＝0.5， v3＝v2x＋a2＝0.498 27；‎ a1＝1， v4＝v3x＋a1＝0.900 35；‎ a0＝1， v5＝v4x＋a0＝0.819 93；‎ 所以f(－0.2)＝0.819 93.‎ ‎【点拨】秦九韶算法是多项式求值的最优算法，特点是：‎ ‎(1)将高次多项式的求值化为一次多项式求值；‎ ‎(2)减少运算次数，提高效率；‎ ‎(3)步骤重复实施，能用计算机操作.‎ ‎【变式训练2】用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1当x＝2时的值为　　　　.‎ ‎【解析】1 397.‎ 题型三　进位制之间的转换 ‎【例3】(1)将101 111 011(2)转化为十进制的数；‎ ‎(2)将53(8)转化为二进制的数.‎ ‎【解析】(1)101 111 011(2)＝1×28＋0×27＋1×26＋1×25＋1×24＋1×23＋0×22＋1×21＋1＝379.‎ ‎(2)53(8)＝5×81＋3＝43.‎ ‎ ‎ 所以53(8)＝101 011(2).‎ ‎【点拨】将k进制数转换为十进制数，关键是先写成幂的积的形式再求和，将十进制数转换为k进制数，用“除k取余法”，余数的书写是由下往上，顺序不能颠倒，k进制化为m进制(k，m≠10)，可以用十进制过渡.‎ ‎【变式训练3】把十进制数89化为三进制数.‎ ‎【解析】具体的计算方法如下：‎ ‎89＝3×29＋2，‎ ‎29＝3×9＋2，‎ ‎9＝3×3＋0，‎ ‎3＝3×1＋0，‎ ‎1＝3×0＋1，‎ 所以89(10)＝10 022(3).‎ 总结提高 ‎1.辗转相除法和更相减损术都是用来求两个数的最大公约数的方法.其算法不同，但二者的原理却是相似的，主要区别是一个是除法运算，一个是减法运算，实质都是一个递推的过程.用秦九韶算法计算多项式的值，关键是正确的将多项式改写，然后由内向外，依次计算求解.‎ ‎2.将k进制数转化为十进制数的算法和将十进制数转化为k进制数的算法操作性很强，要掌握算法步骤，并熟练转化；要熟练应用“除基数，倒取余，一直除到商为‎0”‎.‎