- 2021-05-13 发布 |
- 37.5 KB |
- 3页


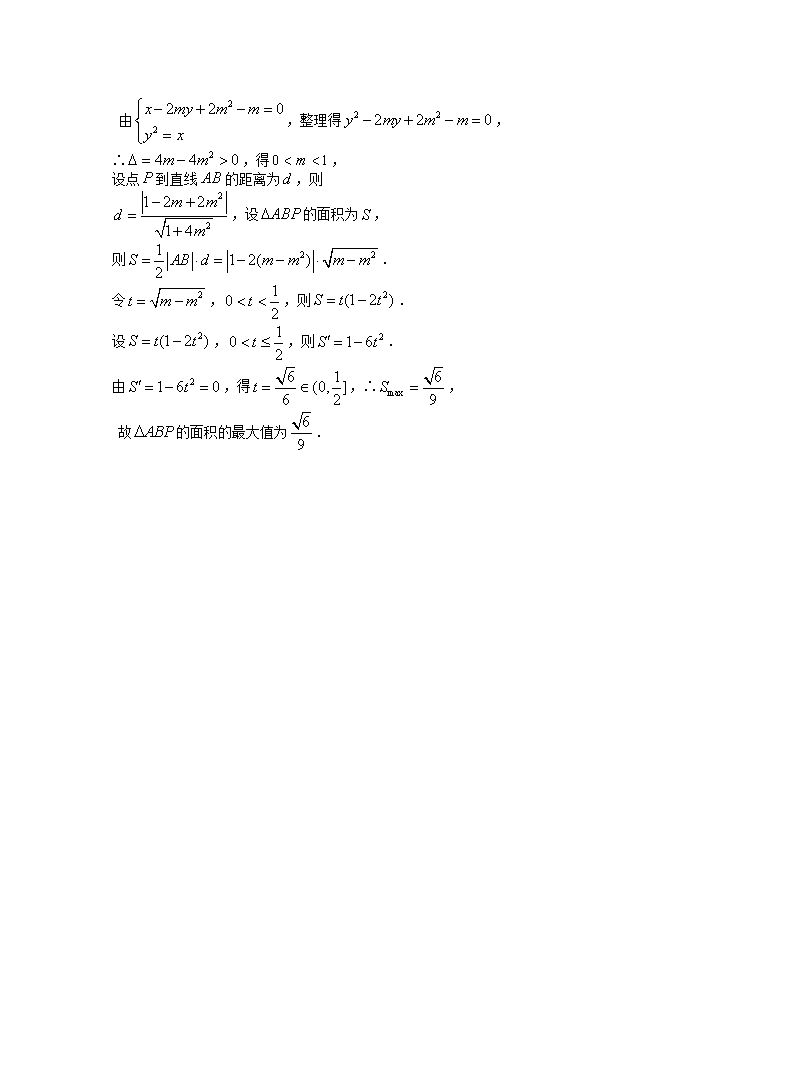
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三维设计广东文人教版2014高考数学第一轮复习考案 抛物线 文
第67课 抛物线 1.(2019四川高考)已知抛物线关于轴对称,它的顶点在坐标原点,并且经过点.若点到该抛物线焦点的距离为,则( ) A. B. C. D. 【答案】B 【解析】可设抛物线方程为, ∵点到该抛物线焦点的距离为, ∵点在抛物线上,∴, 2.(2019安徽高考)过抛物线的焦点的直线交抛物线于两点,点是原点,若,则的面积为( ) 【答案】C 【解析】∵,∴,∴,,取, 3.(2019新课标高考)等轴双曲线的中心在原点,焦点在轴上,与抛物线的准线交于两点,,则双曲线的实轴长为( ) A. B. C. D. 【答案】C 【解析】由题设知抛物线的准线为:, 设等轴双曲线方程为:, 将代入双曲线方程得, 解得,∴实轴长,选C. 4.(2019福建高考)已知双曲线的右焦点与抛物线的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ) A. B. C. D. 【答案】A. 【解析】∵抛物线的焦点坐标为,∴,∴, ∴双曲线的渐进线方程为,即, ∴,故选A. 5.(2019深圳二模)已知抛物线:的焦点为,过点作直线交抛物线于、两点;椭圆的中心在原点,焦点在轴上,点是它的一个顶点,且其离心率. (1)求椭圆的方程; (2)经过、两点分别作抛物线的切线、,切线与相交于点. 证明:. 【解析】(1)设椭圆的方程为,半焦距为. M B A F O 由已知条件,得, ∴,解得. . ∴椭圆的方程为:. (2)显然直线的斜率存在, 否则直线与抛物线只有一个交点,不合题意, 故可设直线的方程为, 由,得, ∵抛物线的方程为,求导得, ∴过抛物线上、两点的切线方程分别是 即 ,, 解得两条切线、的交点的坐标为 ,即. 6.(2019浙江高考)如图,在直角坐标系中,点到抛物线:()的准线的距离为.点是上的定点,是上的两动点,且线段被直线平分. (1)求,的值. (2)求面积的最大值. 【解析】(1)由题意得,得. (2)由(1)可知直线的方程为,设, ∵线段被直线平分. ∴可设线段的中点坐标为 由题意得,设直线的斜率为. 由(1)可知抛物线方程为 由,得, ∴,得, ∴直线的方程为,即. 由,整理得, ∴,得, 设点到直线的距离为,则 ,设的面积为, 则. 令,,则. 设,,则. 由,得,∴, 故的面积的最大值为.查看更多